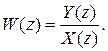В инженерной практике для описания динамических звеньев дискретных САУ (объектов управления, регуляторов, фильтров и т. п.) применяют дискретные передаточные функции вида
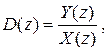 (10.9)
(10.9)
где X (z), Y (z) – соответственно входная и выходная переменные дискретного звена. Заметим, что практически реализуемые дискретные передаточные функции должны иметь порядок полинома знаменателя больше порядка полинома числителя.
Способы получения дискретной передаточной функции:
1). Прямой способ (прямое дискретное преобразование Лапласа):
|
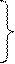 x (t)
x (t) 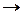 x (kT)
x (kT) 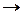 X (z)
X (z) 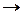
y (t) 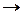 y (kT)
y (kT) 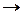 Y (z)
Y (z) 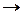
Чтобы получить прямое дискретное преобразование Лапласа сигнала x (t), необходимо заменить этот сигнал дискретными значениями x (kT). Каждое значение x (kT) домножить на z - k, а затем полученный степенной ряд свернуть в конечную сумму (10.7), которая по сути представляет собой дискретное преобразование Лапласа X (z). Аналогично получают прямое дискретное преобразование Лапласа сигнала y (t). Прямое z -преобразование является однозначным преобразованием.
|
|
|
2). С помощью таблицы z -преобразований.
В табл. 10.1 приведено z-преобразование наиболее часто встречающихся в САУ функций.
Табл. 10.1
| x (t) | X (p) | X (z) |
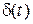
| ||
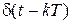
| 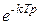
| 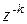
|
| 1(t) | 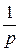
| 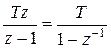
|
| t | 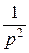
| 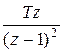
|
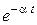
| 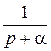
| 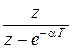
|
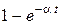
| 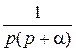
| 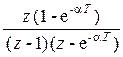
|
sin 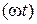
| 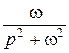
| 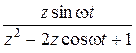
|
cos 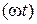
| 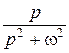
| 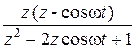
|
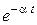 sin sin 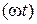
| 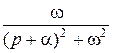
| 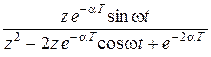
|
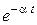 cos cos 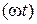
| 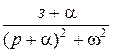
| 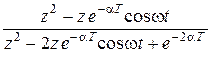
|
3). Через импульсную переходную характеристику
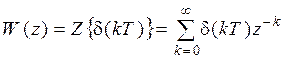 .
.
Замечание: эти преобразования относятся к дискретным системам без фиксатора (экстраполятора).
Следует отметить, что, хотя прямое преобразование Лапласа является однозначным, одно и то же динамическое звено может иметь бесчетное число дискретных передаточных функций в зависимости от применяемого метода экстраполяции. В частности, интегрирующее звено может быть представлено следующими дискретными передаточными функциями:
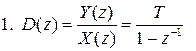 ; (10.10)
; (10.10)
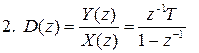 , (10.11)
, (10.11)
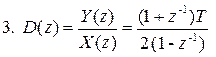 , (10.12)
, (10.12)
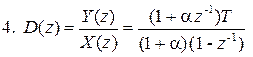 , (10.13)
, (10.13)
где T – такт квантования, 0 £ a £ 1.
Первая и вторая передаточные функции получены с применением экстраполяции нулевого порядка (метода прямоугольников), причем оценка производной выходного сигнала осуществляется соответственно в k -й и
(k -1)-й моменты времени.
Третья передаточная функция получена с применением метода Тастина (метода трапеций), причем усредненная оценка производной выходного сигнала осуществляется по двум точкам – в k -й и (k -1)-й моменты времени.
Четвертая передаточная функция (семейство передаточных функций) получена на основе метода прямоугольников со смещенной оценкой производной выходного сигнала (a = var).
Дискретные передаточные функции дифференцирующего звена могут быть получены из приведенных выше путем перестановки полиномов числителя и знаменателя.
К дискретным передаточным функциям и соответствующим структурным схемам применимы те же аправила структурных преобразований, что и для непрерывных систем.
|
|
|
Для синтеза систем управления реального времени, исследования цифровых систем управления во временной области используют разностные уравнения. Если известна дискретная передаточная функция какого-либо звена, то получение разностного уравнения не представляет труда. В частности, разностные уравнения, описывающие процессы в интегрирующих звеньях (формулы 10.10…10.13), имеют вид:
1. Y (kT) = Y ((k -1) T) + TX (kT);
2. Y (kT) = Y ((k -1) T) + TX ((k -1) T);
3. Y (kT) = Y ((k -1) T) + 0,5 T [ X (kT) + X ((k -1) T)];
4. Y (kT) = Y ((k -1) T) + (T / (1+ a)) [ X (kT) + a X ((k -1) T)].
В пространстве состояний цифровые (импульсные) системы управления представляют либо в виде векторно-матричных разностных уравнений, либо в виде структурных схем с дискретным временем (схем пространства состояний) [2].
 2015-03-22
2015-03-22 5135
5135