Теория вероятностей – это раздел математики, изучающий количественные закономерности случайных явлений, т.е. таких, которые при неоднократном воспроизведении в одинаковых условиях могут протекать по разному. Объектами, которыми оперирует теория вероятностей, являются:
- Случайное событие – всякий факт, который может произойти или не произойти в результате случайного явления;
- случайная величина – некоторое числовое значение появляющееся в результате случайного явления.
Задача 7. Дано вероятность попадания по мишени – 0,3. Требуется определить вероятность попадания с третьего раза.
Решение: Последнее событие наступает при одновременном наступлении: 1) первый раз промахнулся; 2) второй раз промахнулся; 3) третий раз попал.
p(Ā Ā A) = p(Ā)´p(Ā)´p(A)=0,7´0,7´0,3 = 0,147
Задача 8. Дано среди 10 шаров 2 – черные. Требуется определить вероятность с двух попыток вытащить оба этих шара?
Решение. Обозначив A – первый раз вытащить черный, B - второй раз вытащить черный: p (оба раза - черные) = p (AB) = p (A) ´ p (B | A) = 2/10 ´ 1/9 = 1/45
|
|
|
Задача 9. Дано среди 10 шаров 1 – черный. Десять человек по очереди вытаскивают шар. Требуется определить у кого из них наибольшая вероятность вытащить черный?
Решение. Обозначив A 1 – первый вытащил черный шар,... p (A 1) = 1/10; p (второму достался черный) = p (Ā 1 A 2) = p (Ā 1) ´ p (A 2 / Ā 1) = 9/10 ´ 1/9 = 1/10; p (третьему достался черный) = p (Ā 1 Ā 2 A 3) = p (Ā 1) ´ p (Ā 2 / Ā 1) ´ p (A 3 / Ā 2 Ā 1) = 9/10 ´ 8/9´ 1/8 = 1/10 и т.д.,
т.е. все участники розыгрыша имеют одинаковые шансы вытащить черный шар независимо от порядка вытаскивания.
Задача 10. Дано участники группы захвата и группы поддержки атакуют преступников и производят по месту их укрытия две независимые очереди из автоматического оружия. Вероятность поразить цель первой очередью равна 0,2, второй - 0,3. Если преступники не поражены, то они оказывают вооруженное сопротивление и поражают участников операции с вероятностью 0,25. Требуется определить вероятность потерь среди участников операции при условии, что преступники не поражены.
Решение: 1. При использовании теоремы сложения и умножения вероятностей можно определить вероятность поражения от применения оружия с обеих сторон - сотрудников органов внутренних дел и преступников.
2. Вероятность не поражения преступников первой очередью:
Р1 = 1 - 0,2 = 0,8;
3. Вероятность не поражения преступников второй очередью:
Р2 = 1 - 0,3 = 0,7;
4. Вероятность не поражения преступников:
Р = Р1*Р2 = 0,8*0,7 = 0,56;
5. Вероятность поражения преступников
1 - Р = 1 - 0,56 = 0,44.
6. Вероятность потерь среди участников операции:
Р*0,25 = 0,56*0,25 = 0,14.
Задача 11. Дано всхожесть семян данного растения составляет 90 %. Требуется найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.
|
|
|
Решение. 1. Если производится п независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна р, а вероятность противоположного события 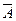 равна q=1-p, то вероятность Рп(т) того, что при этом событие А осуществляется ровно т раз, вычисляется по формуле Бернулли
равна q=1-p, то вероятность Рп(т) того, что при этом событие А осуществляется ровно т раз, вычисляется по формуле Бернулли
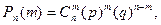 (1)
(1)
где 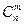 есть число сочетаний из п элементов по т.
есть число сочетаний из п элементов по т.
2. По условию задачи вероятность всхожести семян р =0,9; тогда q =0,1; в данном случае п =5 и т =4. Подставляя эти данные в формулу Бернулли (1), получают
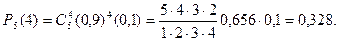
3. Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом, Р(А)=Р5(4)+Р5(5). Первое слагаемое уже найдено. Для вычисления второго снова применяют формулу (1):
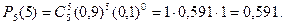
Следовательно, Р(А)=0,328+0,591=0,919.
Задача 12. Дано вероятность появления события А в каждом из 625 испытаний равна 0,64. Требуется найти вероятность того, что событие А в этих испытаниях появиться ровно 415 раз.
Решение. 1. Если число испытаний п велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях применяют приближенную формулу, которая выражает суть локальной теоремы Лапласа.
Если вероятность наступления события А в каждом из п независимых испытаний постоянна и равна р, а число п достаточно велико, то вероятность Рп(т) того, что в этих испытаниях событие А наступит т раз (безразлично, в какой последовательности) вычисляется приближенно по формуле
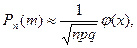 (2)
(2)
где 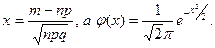
Имеются готовые таблицы значений функции j(х) (табл. П.1).
2. Для х >5 считают, что j(х)»0. Так как функция j(х) четная, то j(-х)=j(х). По условию задачи п =625, т =415, р =0,64. Находят q =1-0,64=036. Определяют значение х при этих данных:
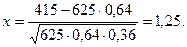
3. По табл. П1 находят, что j(1,25) =0,1826. Подставив это значение в (2), получают
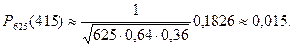
Задача 13. Дано среди семян ржи 0,04 % сорняков. Требуется определить вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?
Решение. 1. Применение асимптотической формулы (2) для случая, когда вероятность р близка к нулю, приводит к значительному отклонению от точного значения Рп(т). При малых значениях р (и при малых значениях q) применяют асимптотическую формулу Пуассона.
Если вероятность появления события А в каждом из п независимых испытаний мала, а число испытаний п достаточно велико, то вероятность того, что событие А наступит т раз, вычисляется приближенно по формуле
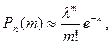 (3)
(3)
где l =пр.
Формулу (3) применяют в тех случаях, когда l £10. При этом чем больше число п и меньше число р, тем точнее результат по этой формуле.
2. По условию задачи п =5000, т =5, р =0,0004. Тогда l =5000.0,0004=2. Применяя (3), получают
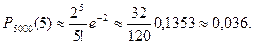
Задача 14. Дано: имеются три одинаковых на вид урны. В них находятся:
в первой урне – 2 белых и 1 черный шар;
во второй урне – 3 белых и 1 черный шар;
в третьей урне – 2 белых и 2 черных шара.
Требуется:
- некто выбирает наугад одну из урн и вынимает из нее шар, найти вероятность того, что это шар белый.
- из случайно выбранной урны вытащен белый шар, найти вероятность того, что он вытащен из второй урны.
Решение. 1. Рассматривают три гипотезы:
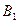 - выбор первой урны,
- выбор первой урны,
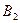 - выбор второй урны,
- выбор второй урны,
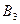 - выбор третьей урны,
- выбор третьей урны,
и событие А - появление белого шара.
2.По условию гипотезы равновозможны, следовательно, их вероятности равны
Р(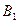 )=Р(
)=Р(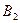 )=Р(
)=Р(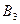 )=
)= 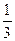 .
.
3. Найдем условные вероятности события А при этих гипотезах:
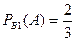 ;
; 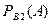
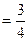 ;
; 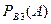
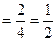 .
.
4. Так как гипотезы 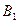 ,
, 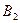 и
и 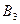 - несовместны и образуют полную группу, то для расчета требуемой вероятности события А применима формула полной вероятности:
- несовместны и образуют полную группу, то для расчета требуемой вероятности события А применима формула полной вероятности:
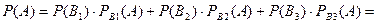
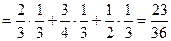 .
.
5. Вероятность того, что белый шар вытащен из второй урны, рассчитаем по формуле Байеса:
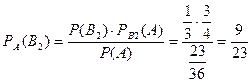 .
.
 2015-03-22
2015-03-22 7494
7494
