2015-03-08
1784
1.1.1. Определение. Пусть R ¾ множество действительных чисел. Линейным пространством над R называется множество V, элементы которого можно складывать (то есть для любых элементов x и у из V ставится в соответствие однозначно элемент x + у из V) и умножать на число (то есть для любых числа a и x из V ставится в соответствие однозначно элемент ax из V), при этом выполняются следующие свойства:
1. Для любых x и y из V
x + y = y + x.
2. Для любых x, y и z из V
(x + y)+ z = x +(y + z).
3. В V существует такой элемент 0 V, что для любого x из V
x +0 V = x.
4. Для любого x из V существует y Î V такой, что
x + y =0 V.
5. Для единицы 1 из R и любого x из V
1 x = x.
6. Для любых чисел a, b и x из V
a (b x)=(ab) x.
7. Для любых чисел a, b и x из V
(a + b) x = ax + bx.
8. Для любых числа a и x, y из V
a (x + y)= ax + ay.
Элементы линейного пространства называются векторами, а само линейное пространство иногда называется векторным пространством. Элемент 0 V из условия 3) называется нулевым вектором линейного пространства V, элемент y из условия 4) называется противоположным к x и обозначается через - x.
|
|
|
Условия 1 - 8 из определения называются аксиомами линейного пространства. При этом важно не только то, что векторы можно складывать и умножать на число, но и то, что результаты сложения и умножения на число снова принадлежат V: для любых числа a и x, у Î V снова имеем x + у Î V и ax Î V.
В обозначении нуля 0 V векторного пространства обычно индекс V опускается, так как из контекста обычно ясно, о каком нуле идёт речь.
1.1.2. Примеры. I. Рассмотрим множество C (a, b) непрерывных на интервале (a, b) функций действительной переменной. Относительно сложения и умножения на число это множество образует линейное пространство над R. Действительно, как известно, если f, g Î C (a, b) (то есть функции f и g - непрерывны на интервале C (a, b)) то f + g Î C (a, b) и af Î C (a, b) для любого числа a (то есть функции f + g и af - снова непрерывные на интервале C (a, b) функции). При этом выполнены все аксиомы 1 - 8 линейного пространства:
1. Для любых f и g из C (a, b)
f + g = g + f.
2. Для любых f, g и h из C (a, b)
(f + g)+ h = f +(g + h).
3. В C (a, b) существует такой элемент 0 C ( a , b ), что для любого f из C (a, b)
f +0 C ( a , b )= f.
Ясно, что 0 C ( a , b ) - нулевая функция: 0 C ( a , b )(х)=0 для любого х Î R.
4. Для любого f из C (a, b) существует g Î C (a, b) такой, что
f + g =0 C ( a , b ).
Ясно, что роль противоположной функции к f играет функция - f.
5. Для единицы 1 из R и любого f из C (a, b)
1 f = f.
6. Для любых чисел a, b и функции f из C (a, b)
a (bf)=(ab) f.
7. Для любых чисел a, b и функции f из C (a, b)
(a + b) f = af + bf.
8. Для любых числа a и функций f, g из C (a, b)
a (f + g)= af + ag.
II.Пусть An ¾ множество всех упорядоченных наборов чисел:
An ={(a 1, a 2, …, an)| ai Î R, i =1, …, n }.
Тогда An относительно операций сложения и умножения на число a, определённых соответственно по правилам
|
|
|
(a 1, a 2, …, an)+(b 1, b 2, …, bn)=(a 1+ b 1, a 2+ b 2, …, an + bn),
a (a 1, a 2, …, an)=(aa 1, aa 2, …, aan)
образует линейное пространство над R, которое называется арифметическим линейным пространством над R. Действительно, для любых элементов (a 1, a 2, …, an) и (b 1, b 2, …, bn) их сумма (a 1+ b 1, a 2+ b 2, …, an + bn) и произведение (aa 1, aa 2, …, aan) на число a лежат в An. Далее:
1. Для любых 
=(a 1, a 2, …, an) и 
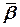=(b 1, b 2, …, bn) имеем
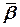+ =(a 1, a 2, …, an)+(b 1, b 2, …, bn)=(a 1+ b 1, a 2+ b 2, …, an + bn) =
=(b 1+ a 1, b 2+ a 2, …, bn + an)=(b 1, b 2, …, bn)+(a 1, a 2, …, an)= + ,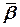
то есть для любых и 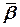из An имеем
+ = + .
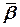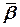2. Для любых =(a 1, a 2, …, an), 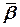=(b 1, b 2, …, bn) и 
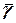=(g 1, g 2, …, gn) имеем
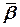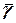( + )+ =((a 1, a 2, …, an)+(b 1, b 2, …, bn))+(g 1, g 2, …, gn)=
(a 1+ b 1, a 2+ b 2, …, an + bn)+(g 1, g 2, …, gn) =
=((a 1+ b 1)+ g 1, (a 2+ b 2)+ g 2, …, (an + bn)+ gn)=
=(a 1+(b 1+ g 1), a 2+(b 2+ g 2), …, an +(bn + gn))=
=(a 1, a 2, …, an)+(b 1+ g 1, b 2+ g 2, …, bn + gn) = +( + ),
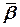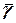то есть для любых , 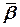и 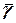из An имеем ( + )+ = +( + ).
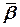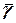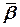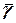3. Роль нулевого вектора играет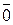 
=(0, 0, …, 0), где 0 - нуль: для любого =(a 1, a 2, …, an) имеем
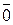+ =(a 1, a 2, …, an)+(0, 0, …, 0)=(a 1+0, a 2+0, …, an +0)=(a 1, a 2, …, an),
то есть + = .
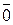4. Для вектора =(a 1, a 2, …, an) ему противоположным - будет являться (- a 1, - a 2, …, - an):
+(- )=(a 1, a 2, …, an)+(- a 1, - a 2, …, - an)=(a 1+(- a 1), a 2+(- a 2), …, an +(- a n))=
=(0, 0, …, 0)= ,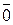
то есть +(- )= .
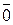5. Для единицы 1 из R и любого из An имеем
1 =1(a 1, a 2, …, an)=(1 a 1, 1 a 2, …, 1 an)=(a 1, a 2, …, an)= ,
то есть 1 = .
6. Для любых a и b из R и =(a 1, a 2, …, an) из An имеет место
a (b )= a (ba 1, ba 2, …, ban)=(a (ba 1), a (ba 2), …, a (ban))=
=((ab) a 1, (ab) a 2, …, (ab) an)=(ab)(a 1, a 2, …, an)=(ab) ,
то есть a (b )=(ab) .
7. Для любых a и b из R и =(a 1, a 2, …, an) из An имеет место
(a + b) =((a + b) a 1, (a + b) a 2, …, (a + b) an)=(aa 1+ ba 1, aa 2+ ba 2, …, aan + ban)=
=(aa 1, aa 2, …, aan)+(ba 1, ba 2, …, ban)= a (a 1, a 2, …, an)+ b (a 1, a 2, …, an)= a + b ,
то есть (a + b) = a + b .
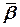8. Для любых a из R и =(a 1, a 2, …, an) и =(b 1, b 2, …, bn) из An имеет место
a ( + 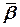)= a (a 1+ b 1, a 2+ b 2, …, an + bn)=(a (a 1+ b 1), a (a 2+ b 2), …, a (an + bn))=
(aa 1+ ab 1, aa 2+ ab 2, …, aan + abn)=(aa 1, aa 2, …, aan)+(ab 1, ab 2, …, abn)=
= a (a 1, a 2, …, an)+ a (b 1, b 2, …, bn)= a + a ,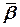
то есть 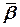a ( + )= a + a .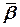
III. Множество всех матриц фиксированной размерности m ´ n образует линейное пространство. Действительно, в результате сложения двух матриц размерности m ´ n и умножения такой же матрицы на число получается матрица размерности m ´ n. При этом сложение матриц и умножение матрицы на число обладает всеми 8 свойствами из определения линейного пространства (см. Алгебра-I, Гл. I). Это линейное пространство будем обозначать верез Mm ´ n (R). Например, множество матриц 2´2 образует линейное пространство M 2´2(R). Множество матриц 2´3 - это уже другое линейное пространство M 2´3(R). По существу, An - линейное пространство M 1´ n (R) матриц размерности 1´ n.
1.2. Простейшие свойства линейного пространства. Из введённого определения линейного пространства вытекают его простейшие свойства.
1.2.1. Предложение. Справедливы следующие простейшие свойства линейного пространства:
1. Нулевой нулевой вектор 0 V единствен.
2. Для любого вектора a его противоположный вектор - a единствен.
3. Для любого вектора a
-(- a)= a.
4. Для любых векторов a и b линейного пространства
-(a + b)=(- a)+(- b).
5. Для любых векторов a, b линейного пространства уравнения x + a = b и a + x = b имеют единственное решение b +(- a).
1.2.2. Определение. Для векторов a и b пространства V элемент b +(- a) обозначается через b - a и называется разностью векторов b и a.
В связи с введённым определением свойство 4 предложения 1.2.1 принимает вид -(a + b)=- a - b.
Отметим, что эти свойства выполняются для любых множеств, элементы которого можно складывать, и при этом выполняются аксиомы 1 - 4. Кроме сформулированных этих свойств линейного пространства можно сформулировать и доказать следующие простейшие свойства, специфичные для линейных пространств (специфика заключается в возможности элементы линейного пространства умножать на числа).
1.2.3. Теорема. Справедливы следующие (дальнейшие) простейшие свойства линейного пространства V:
|
|
|
1. В произвольном линейном пространстве сумма вида (...((x 1+ x 2)+ x 3)+...)+ xs не зависит от расстановки скобок. Поэтому в такого рода суммах скобки принято опускать: x 1+ x 2+...+ xs -1+ xs.
2. Для любого x Î V имеет место равенство 0 x =0 V.
3. Для любого a Î R имеет место равенство a 0 V =0 V.
4. Если ax =0 V, то либо a =0, либо x =0 V.
5. Для любого x Î V и a Î R имеет место равенство (- a) x = -(ax), в частности, (-1) x = - x.
6. Для любых a, a 1, a 2, …, an Î R и x, x 1, x 2, …, xn Î V имеют место равенства (± a 1± a 2±…± an) x =± a 1 x ± a 2 x ±…± anx
и
a (± x 1± x 2±…± xn)= ± ax 1± ax 2±…± axn.
7. Для любых x 1, x 2, …, xn Î V имеет место равенство
-(x 1+ x 2+…+ xn)=- x 1- x 2-…- xn.
