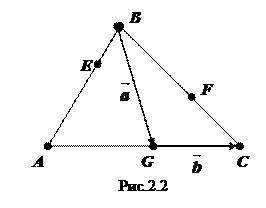 1) Дан треугольник ABCD. Точки E, F и G делят в отношении l стороны AB, BC и AC, соответственно (рис 2.2). Выразить
1) Дан треугольник ABCD. Точки E, F и G делят в отношении l стороны AB, BC и AC, соответственно (рис 2.2). Выразить  ,
, 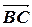 и
и  через
через  =
= 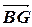 ,
,  =
= 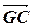 :
:
а) l =2; б) l =3; в) l = 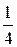 .
.
Решение. а) Выразить  через
через  и
и  означает представить
означает представить  в виде линейной комбинации векторов
в виде линейной комбинации векторов  и
и  :
:  = a
= a  + b
+ b  , причём в этом представлении определить a и b. Имеем
, причём в этом представлении определить a и b. Имеем  =
= 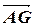 +
+ 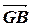 . Ясно, что
. Ясно, что 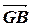 =-
=-  . Далее, так как
. Далее, так как 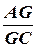 = l =2, то AG =2 GC, то есть
= l =2, то AG =2 GC, то есть 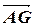 =2
=2 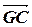 =2
=2  . Отсюда
. Отсюда  =2
=2  +(-
+(-  ), то есть
), то есть  =-
=-  +2
+2  .
.
Очевидно, 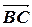 =
= 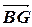 +
+ 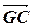 =
=  +
+  , то есть
, то есть 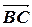 =
=  +
+  .
.
Наконец,  =
= 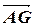 +
+ 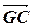 =2
=2  +
+  =3
=3  , то есть
, то есть  =3
=3  .
.
Ответ: а)  =-
=-  +2
+2  ;
; 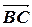 =
=  +
+  ;
;  =3
=3  .
.
2) Найти линейную зависимость между векторами:
а)  =(4; 1),
=(4; 1),  =(1; 1),
=(1; 1),  =(2; -1);
=(2; -1);
б)  =(3; -1),
=(3; -1),  =(-2; 2),
=(-2; 2),  =(5; -8);
=(5; -8);
в)  =(3; -1; 2),
=(3; -1; 2),  =(2; 1; 1),
=(2; 1; 1),  =(1; -1; 2),
=(1; -1; 2),  =(4; 8; 3);
=(4; 8; 3);
г)  =(1; -1; 1),
=(1; -1; 1),  =(2; 1; -1),
=(2; 1; -1),  =(1; 2; 3),
=(1; 2; 3),  =(4; 2; 3).
=(4; 2; 3).
Решение. а) Найти линейную зависимость между векторами  ,
,  и
и  - это значит найти a, b и g, не все равные нулю, в выражении
- это значит найти a, b и g, не все равные нулю, в выражении
a  + b
+ b  + g
+ g  =
=  . (2.1)
. (2.1)
Имеем
a  + b
+ b  + g
+ g  = a (4; 1)+ b (1; 1)+ g (2; -1)=(4 a + b +2 g; a + b - g)
= a (4; 1)+ b (1; 1)+ g (2; -1)=(4 a + b +2 g; a + b - g)
(по 2.1.4). Так как  =(0, 0), то (4 a + b +2 g; a + b - g)=(0, 0). Два вектора равны тогда и только тогда, когда их координаты совпадают. Поэтому приходим к однородной системе
=(0, 0), то (4 a + b +2 g; a + b - g)=(0, 0). Два вектора равны тогда и только тогда, когда их координаты совпадают. Поэтому приходим к однородной системе
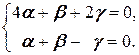
Решаем её:
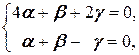 Û
Û 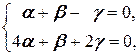 Û
Û 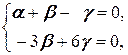 Û
Û 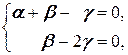
Û 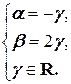
Таким образом, равенство (2.1) принимает вид - g  +2 g
+2 g  + g
+ g  =
=  , где g ≠0. Тогда g (-
, где g ≠0. Тогда g (-  +2
+2  +
+  )=
)=  . Так как g ≠0, то по свойству 6 векторов -
. Так как g ≠0, то по свойству 6 векторов -  +2
+2  +
+  =
=  . Это и есть искомая линейная зависимость между векторами
. Это и есть искомая линейная зависимость между векторами  ,
,  и
и  .
.
|
|
|
в) Требуется найти a, b, g, d в равенстве
a  + b
+ b  + g
+ g  + d
+ d  =
=  . (2.2)
. (2.2)
Имеем
a  + b
+ b  + g
+ g  + d
+ d  = a (3; -1; 2)+ b (2; 1; 1)+ g (1; -1; 2)+ d (4; 8; 3)=
= a (3; -1; 2)+ b (2; 1; 1)+ g (1; -1; 2)+ d (4; 8; 3)=
=(3 a +2 b + g +4 d; - a + b - g +8 d; 2 a + b +2 g +3 d).
С учётом (2.2) приходим к системе и решаем её:
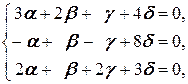 Û
Û 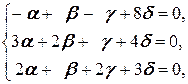 Û
Û 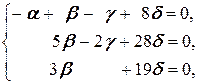 Û
Û 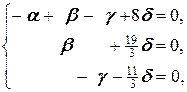 Û
Û 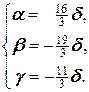
Равенство (2.2) принимает вид 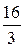 d
d  -
- 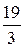 d
d  -
- 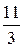 d
d  + d
+ d  =
=  , то есть
, то есть 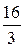
 -
- 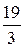
 -
- 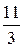
 +
+  =
=  - линейная зависимость между векторами
- линейная зависимость между векторами  ,
,  ,
,  и
и  .
.
Умножая полученную линейную зависимость на 3, можно получить другую (равносильную полученной) линейную зависимость между ними: 16  -19
-19  -11
-11  +3
+3  =
=  .
.
Ответ: а) -  +2
+2  +
+  =
=  ; б) 16
; б) 16  -19
-19  -11
-11  +3
+3  =
=  .
.
3) Проверить линейную зависимость векторов:
а)  =(4; 1),
=(4; 1),  =(1; 1);
=(1; 1);
б)  =(1; 1),
=(1; 1),  =(2; -2);
=(2; -2);
в)  =(2; 1),
=(2; 1),  =(-4; -2);
=(-4; -2);
г)  =(1; 1),
=(1; 1),  =(3; 3);
=(3; 3);
д)  =(3; -1; 2),
=(3; -1; 2),  =(2; 1; 1);
=(2; 1; 1);
е)  =(3; -1; 2),
=(3; -1; 2),  =(2; 1; 1),
=(2; 1; 1),  =(1; -1; 2);
=(1; -1; 2);
ж)  =(1; 2; 3),
=(1; 2; 3),  =(4; 5; 6),
=(4; 5; 6),  =(7; 8; 9);
=(7; 8; 9);
з)  =(1; -1; 1),
=(1; -1; 1),  =(2; 1; -1),
=(2; 1; -1),  =(1; 2; 3).
=(1; 2; 3).
Решение. а) Применим теорему 2.1.5. Так как 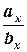 =
= 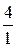 =4,
=4, 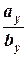 =
= 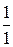 =1, то
=1, то 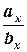 ≠
≠ 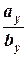 , и координаты векторов
, и координаты векторов  и
и  непропорциональны. Следовательно, векторы
непропорциональны. Следовательно, векторы  и
и  линейно независимы (неколлинеарны).
линейно независимы (неколлинеарны).
в) Имеем 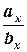 =
= 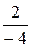 =
= 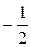 ,
, 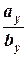 =
= 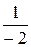 =
= 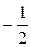 , то есть
, то есть 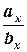 =
= 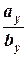 , и векторы линейно зависимы (коллинеарны).
, и векторы линейно зависимы (коллинеарны).
е) Имеем
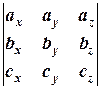 =
= 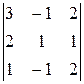 ≠0.
≠0.
Поэтому векторы  ,
,  и
и  линейно независимы (некомпланарны).
линейно независимы (некомпланарны).
ж) Так как
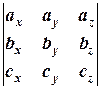 =
= 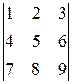 =0,
=0,
то векторы линейно зависимы (компланарны).
4) На плоскости даны векторы  и
и 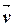 . Доказать, что они образуют базис на плоскости и найти координаты вектора
. Доказать, что они образуют базис на плоскости и найти координаты вектора  в этом базисе:
в этом базисе:
а)  =(4; 1),
=(4; 1), 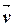 =(1; 1),
=(1; 1),  =(2; -1);
=(2; -1);
б)  =(1; -1),
=(1; -1), 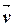 =(-2; 3),
=(-2; 3),  =(-2; -3).
=(-2; -3).
Решение. а) Так как  и
и 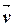 неколлинеарны (см. решение упр 3. а)), то на плоскости они образуют базис (Теорема 2.1.3). Найдём разложение
неколлинеарны (см. решение упр 3. а)), то на плоскости они образуют базис (Теорема 2.1.3). Найдём разложение  в этом базисе, то есть коэффициенты a и b в равенстве
в этом базисе, то есть коэффициенты a и b в равенстве
 = a
= a  + b
+ b 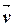 (2.3)
(2.3)
|
|
|
I способ. Распишем правую часть (2.3):
a  + b
+ b 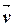 = a (4; 1)+ b (1; 1)=(4 a + b; a + b).
= a (4; 1)+ b (1; 1)=(4 a + b; a + b).
Тогда (2.3) принимает вид (4 a + b; a + b)=(2; -1) и мы приходим к системе 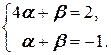
Решаем эту систему:
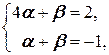 Û
Û 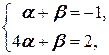 Û
Û 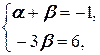 Û
Û 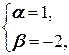
Таким образом,  =
=  -2
-2 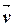 , то есть (1; -2) - координаты вектора
, то есть (1; -2) - координаты вектора  в базисе (
в базисе ( ,
, 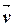 ).
).
II способ. Найдём сначала линейную зависимость между векторами  ,
, 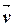 ,
,  : -
: -  +2
+2 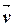 +
+  =
=  (см. решение упр. 2. а)). Отсюда
(см. решение упр. 2. а)). Отсюда  =
=  -2
-2 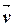 .
.
Ответ: а)  =(1; -2).
=(1; -2).
5) В пространстве даны векторы 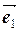 ,
, 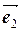 и
и 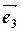 . Доказать, что они образуют базис в пространстве и найти координаты вектора
. Доказать, что они образуют базис в пространстве и найти координаты вектора  в этом базисе:
в этом базисе:
а) 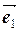 =(3; -1; 2),
=(3; -1; 2), 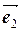 =(2; 1; 1),
=(2; 1; 1), 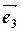 =(1; -1; 2),
=(1; -1; 2),  =(4; 8; 3);
=(4; 8; 3);
б) 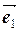 =(3; -1; 2),
=(3; -1; 2), 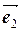 =(2; 1; 1),
=(2; 1; 1), 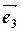 =(5; 0; 2),
=(5; 0; 2),  =(3; -1; 3).
=(3; -1; 3).
Решение. а) Так как векторы 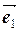 ,
, 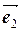 и
и 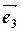 некомплнарны (см. решение упр 3. е)), то в пространстве они образуют базис (Теорема 2.1.3). Найдём разложение
некомплнарны (см. решение упр 3. е)), то в пространстве они образуют базис (Теорема 2.1.3). Найдём разложение  в этом базисе, то есть коэффициенты a 1, a 2 и a 3 в равенстве
в этом базисе, то есть коэффициенты a 1, a 2 и a 3 в равенстве
 = a 1
= a 1 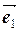 + a 2
+ a 2 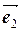 + a 3
+ a 3 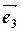 (2.4)
(2.4)
I способ. Распишем правую часть (2.4):
a 1 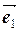 + a 2
+ a 2 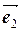 + a 3
+ a 3 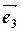 =(3 a 1+2 a 2+ a 3; - a 1+ a 2- a 3; 2 a 1+ a 2+2 a 3).
=(3 a 1+2 a 2+ a 3; - a 1+ a 2- a 3; 2 a 1+ a 2+2 a 3).
Тогда (2.4) принимает вид (3 a 1+2 a 2+ a 3; - a 1+ a 2- a 3; 2 a 1+ a 2+2 a 3)=(1; 2; 1) и мы приходим к системе и решаем её:
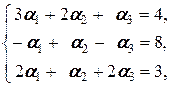 Û
Û 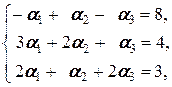 Û
Û
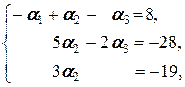 Û
Û 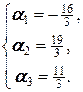
Таким образом,  =-
=- 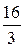
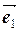 +
+ 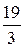
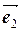 +
+ 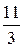
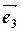 , то есть (-
, то есть (- 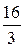 ;
; 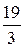 ;
; 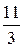 ) - координаты вектора
) - координаты вектора  в базисе (
в базисе (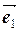 ,
, 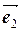 ,
, 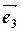 ).
).
II способ. Найдём сначала линейную зависимость между векторами 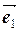 ,
, 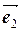 ,
, 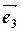 ,
,  :
: 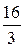
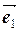 -
- 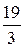
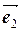 -
- 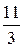
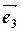 +
+  =
=  (см. решение упр. 3. а)). Отсюда
(см. решение упр. 3. а)). Отсюда  =-
=- 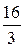
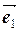 +
+ 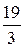
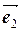 +
+ 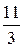
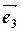 .
.
Ответ: а)  =(-
=(- 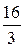 ;
; 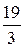 ;
; 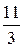 ).
).
Репер.
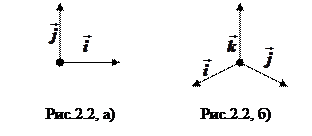 2.2.1. Особый интерес представляют базисы на плоскости и в пространстве, состоящие из попарно ортогональных векторов единичной длины. Они называются реперами (или ортами) на плоскости или в пространстве. Векторы репера на плоскости обозначают через
2.2.1. Особый интерес представляют базисы на плоскости и в пространстве, состоящие из попарно ортогональных векторов единичной длины. Они называются реперами (или ортами) на плоскости или в пространстве. Векторы репера на плоскости обозначают через  и
и 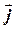 , причём сам репер обозначают в виде упорядоченной пары (
, причём сам репер обозначают в виде упорядоченной пары ( ,
, 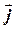 ) (вектор
) (вектор  первым!), и эта пара - правая (рис. 2.2, а)).
первым!), и эта пара - правая (рис. 2.2, а)).
Векторы репера в пространстве обозначают через  ,
, 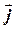 и
и  , сам репер обозначают в виде упорядоченной тройки (
, сам репер обозначают в виде упорядоченной тройки ( ,
, 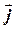 ,
,  ) (вектор
) (вектор  первым,
первым, 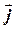 - вторым), и эта тройка - правая (рис. 2.2, б)).
- вторым), и эта тройка - правая (рис. 2.2, б)).
2.2.2. Таким образом, произвольный вектор  на плоскости представим единственным образом в виде
на плоскости представим единственным образом в виде  = a 1
= a 1  + a 2
+ a 2 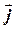 , в пространстве - в виде
, в пространстве - в виде  = a 1
= a 1  + a 2
+ a 2 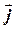 + a 3
+ a 3  , и (a 1, a 2) - координаты вектора
, и (a 1, a 2) - координаты вектора  в репере (
в репере ( ,
, 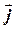 ) на плоскости и (a 1, a 2, a 3) - координаты вектора
) на плоскости и (a 1, a 2, a 3) - координаты вектора  в репере (
в репере ( ,
, 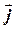 ,
,  ) в пространстве (рис.2.3)
) в пространстве (рис.2.3)
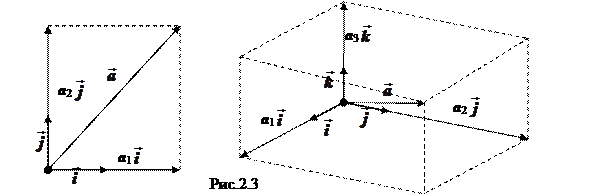
Впредь, если в обозначении вектора через его координаты в некотором базисе не указано, в каком, то будем предполагать, что они заданы в репере.
 2015-03-08
2015-03-08 743
743








