Решить указанную в задании задачу при следующих данных:
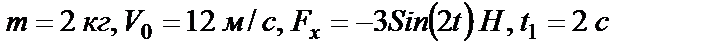 , т.е. определяем
, т.е. определяем 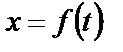 .
.

I. Рассматриваем движение тела D на учачтке АВ, считая его материальной точкой D. Показываем в произвольном положении тело D и действующая на него силы: 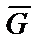 ‑ сила тяжести (
‑ сила тяжести (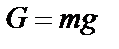 );
); 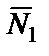 ‑ нормальная составляющая реакции поверхности по которой движется тело;
‑ нормальная составляющая реакции поверхности по которой движется тело; 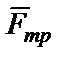 ‑сила трения.
‑сила трения.
Берем систему координат 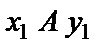 , совмещая начало координат с точкой А, из которой тело начинает движение: ось
, совмещая начало координат с точкой А, из которой тело начинает движение: ось 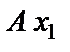 - направляем по движению тела; ось
- направляем по движению тела; ось 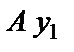 - направляем перпендикулярно к оси
- направляем перпендикулярно к оси 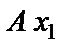 . К решению задачи применяем дифференциальные уравнения движения точки в проекциях на оси координат
. К решению задачи применяем дифференциальные уравнения движения точки в проекциях на оси координат 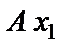 и
и 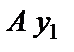 .
.
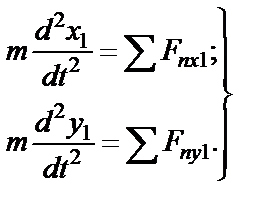
Для удобства составления этих уравнений вектор 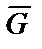 разложим на два составляющих вектора
разложим на два составляющих вектора 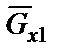 и
и 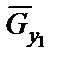 .
.
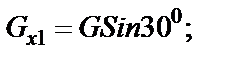
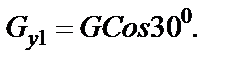
Составляем дифференциальные уравнения движения тела.
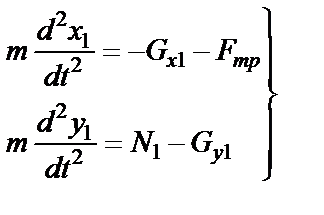 , (20)
, (20)
где 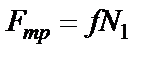 .
.
С учетом выражений для 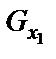 ,
, 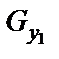 ,
, 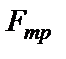 , уравнения (20) примут вид
, уравнения (20) примут вид
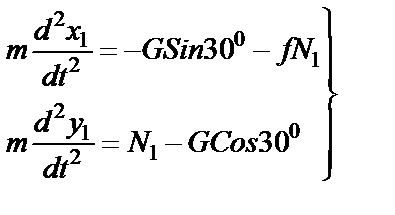 (21)
(21)
Учитывая, что 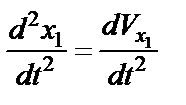 ,
, 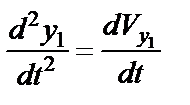 и
и 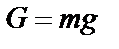 , делаем замену.
, делаем замену.
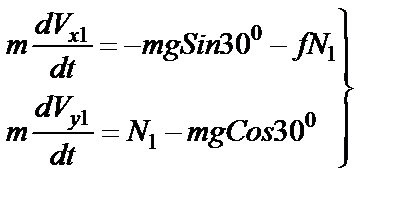 (22)
(22)
Замечаем, что тело движется только по оси 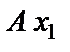 , поэтому
, поэтому
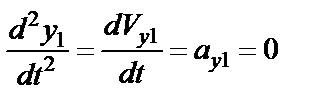
и значит, 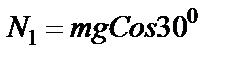 .
.
Делаем подстановку в первое уравнение из уравнений (22)
|
|
|
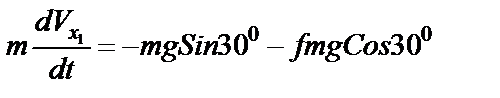 ;
;
Упрощаем:
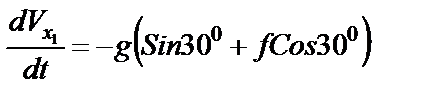 .
.
В числах:
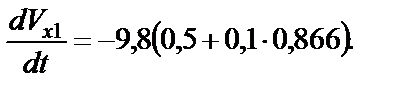
Окончательно получим
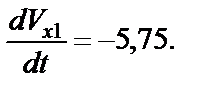 (23)
(23)
Разделяем переменные и интегрируем:
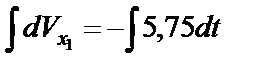
Получаем:
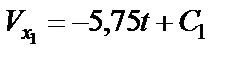 (24)
(24)
Постоянную 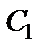 определяем по начальным условиям: при
определяем по начальным условиям: при 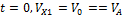 ,т.к. движение началось из точки А.
,т.к. движение началось из точки А.
Подставляем в уравнение (24)
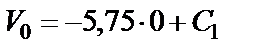 , или
, или 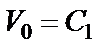 ,
,
уравнение (24) принимает вид:
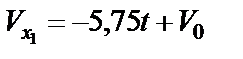 .
.
Зная 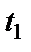 - время движения тела от точки А до точки В, определяем скорость тела в точке В
- время движения тела от точки А до точки В, определяем скорость тела в точке В
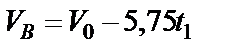 ,
,
с учетом численных значений имеем
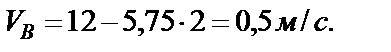
Если в условии задачи дано не время 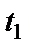 , а l – длина участка АВ, то уравнение (23) следует преобразовать так:
, а l – длина участка АВ, то уравнение (23) следует преобразовать так:
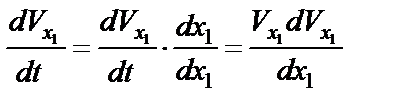 ,
,
окончательно
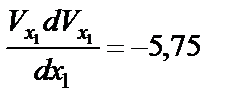 .
.
Затем разделяем переменные и проинтегрируем:
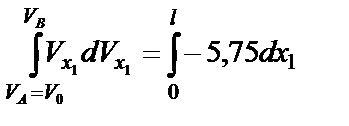 .
.
Получаем
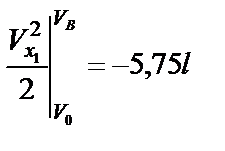 ,
,
Подставляем пределы интегрирования
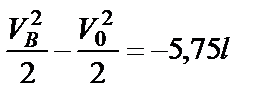
и находим скорость в точке В.
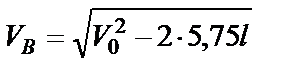 .
.
Допустим 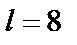 м, тогда
м, тогда
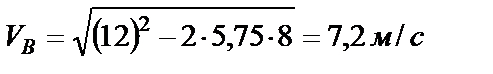 .
.
II. Рассматриваем движение тела на участке ВС.
1. Случай, когда 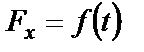 , а именно
, а именно 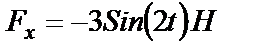 .
.
Показываем тело D в произвольном положении на участке BC и действующие на тело силы (см. рисунок 31): 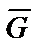 ‑ сила тяжести;
‑ сила тяжести; 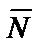 ‑ нормальная составляющая реакции связи;
‑ нормальная составляющая реакции связи; 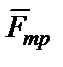 ‑ сила трения;
‑ сила трения; 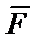 ‑ заданная сила (проекция
‑ заданная сила (проекция 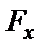 ‑ отрицательная, поэтому силу
‑ отрицательная, поэтому силу 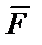 направляем против движения).
направляем против движения).
Показываем систему координат 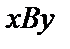 с началом в точке В, ось Вх направляем по движению тела, ось Ву – перпендикулярно к Вх. Движение тела происходит только вдоль оси Вх, поэтому примем что
с началом в точке В, ось Вх направляем по движению тела, ось Ву – перпендикулярно к Вх. Движение тела происходит только вдоль оси Вх, поэтому примем что
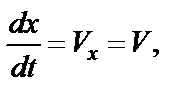 а
а 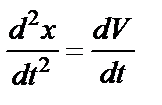 .
.
Составляем дифференциальные уравнения движения тела:
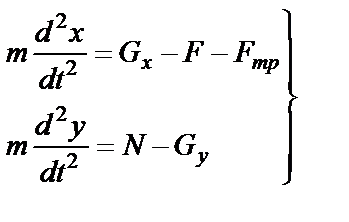 , (25)
, (25)
где
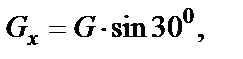
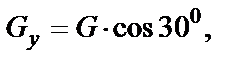
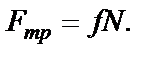
Учитывая, что 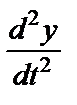 = 0 (движение только по оси Вх), имеем
= 0 (движение только по оси Вх), имеем 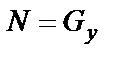 .
.
Делаем подстановку и решаем первое из уравнений (25)
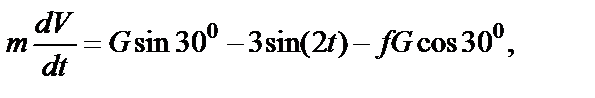
или
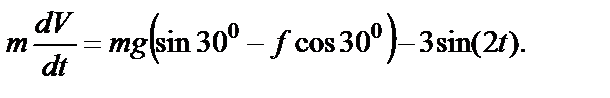
После преобразования получим
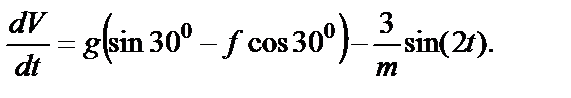
В числах:
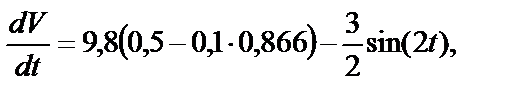
или окончательно
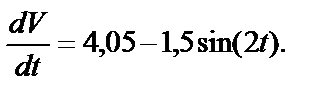
Разделяем переменные и интегрируем:
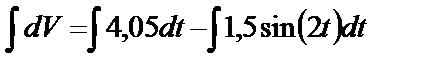 .
.
Получаем:
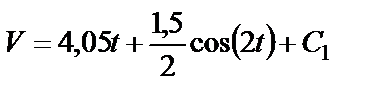 . (26)
. (26)
Постоянную 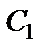 определим по начальным условиям: при
определим по начальным условиям: при 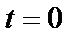
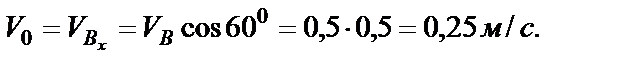
Подставляем 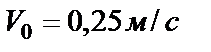 и
и 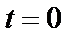 в уравнение (26)
в уравнение (26)
|
|
|
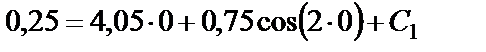 ,
,
откуда
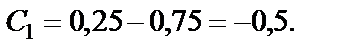
Подставляя значение 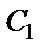 в формулу (26), получаем закон изменения скорости
в формулу (26), получаем закон изменения скорости
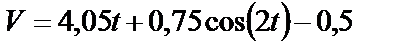 . (27)
. (27)
Делаем замену 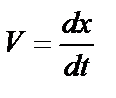 :
:
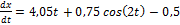 ,
,
разделяем переменные и интегрируем
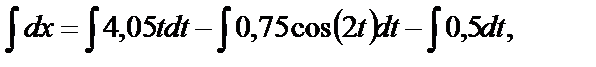
получаем:
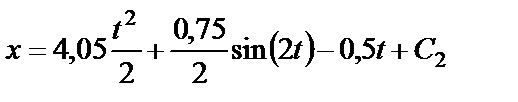 . (28)
. (28)
Постоянную 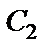 определяем по начальным условиям: при
определяем по начальным условиям: при 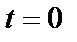
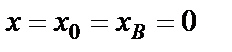 , подставляя их в выражение (28)
, подставляя их в выражение (28)
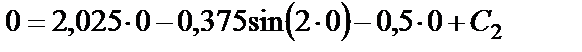 .
.
Откуда 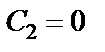 .
.
Окончательно имеем:
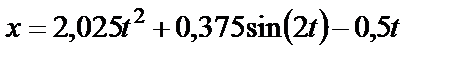 (29)
(29)
это и есть уравнение движения тела на участке ВС.
2. Случай, когда 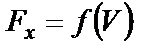 .
.
В рассматриваемом примере на участке ВС на тело действуют те же силы: 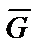 ,
, 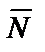 ,
, 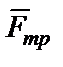 ,
, 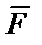 , где
, где 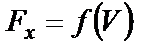 . Допустим, что
. Допустим, что 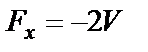 . Расстановка векторов сил и дифференциальные уравнения движения остаются те же, что и в случае
. Расстановка векторов сил и дифференциальные уравнения движения остаются те же, что и в случае 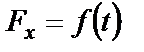 .
.
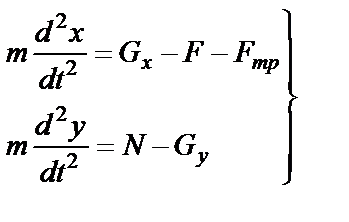 , (30)
, (30)
где силы 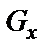 ,
, 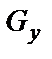 ,
, 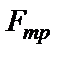 определяются также как показано в случае 1.
определяются также как показано в случае 1.
Учитывая, что 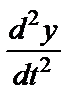 = 0 (движение только по оси Вх), имеем
= 0 (движение только по оси Вх), имеем 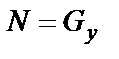 .
.
Решаем первое из системы уравнений (30):
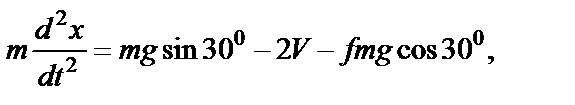
или
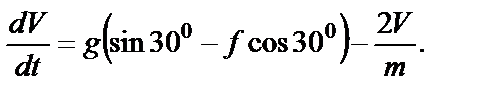
В числах:
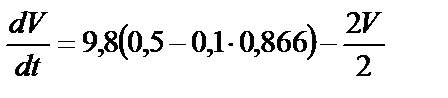
после преобразования имеем
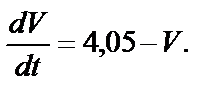
Разделяем переменные и интегрируем:
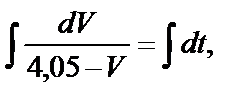
получаем
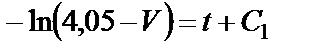 . (31)
. (31)
Постоянную 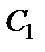 определяем по начальным условиям: при
определяем по начальным условиям: при 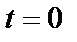
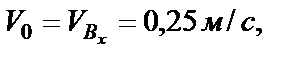 подставляя их в выражение (31), откуда
подставляя их в выражение (31), откуда 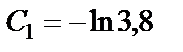 .
.
Теперь найденное значение 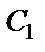 используем в уравнении (31)
используем в уравнении (31)
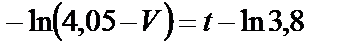
или
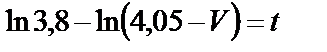 .
.
Решаем:
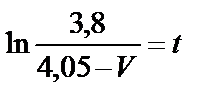 ;
;
после преобразования
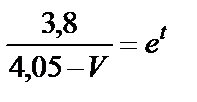 ,
,
или
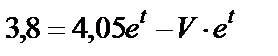 ,
,
откуда:
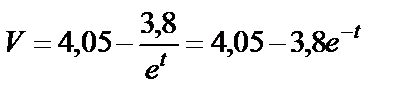 . (32)
. (32)
С учетом 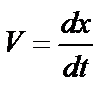 выражение (32) примет вид
выражение (32) примет вид
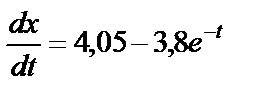 .
.
Разделяем переменные и интегрируем:
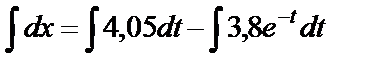 .
.
Получаем:
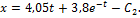 (33)
(33)
Постоянную 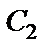 определяем по начальным условиям: при
определяем по начальным условиям: при 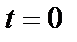
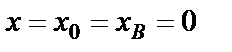 , подставляя их в формулу (33)
, подставляя их в формулу (33)
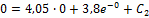 ,
,
откуда 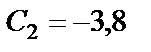 .
.
Уравнение движения тела на участке ВС
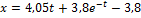 (м)
(м)
3. Случай, когда на участке ВС на тело действует сила 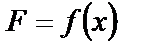 .
.
Допустим 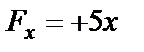 , силу
, силу 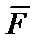 направим по движению тела.
направим по движению тела.
Дифференциальные уравнения будут такие же, как и в рассмотренных выше случаях.
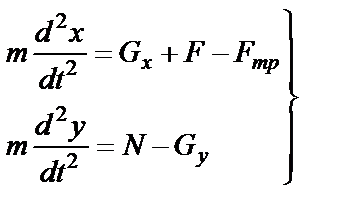 , (34)
, (34)
где силы 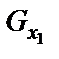 ,
, 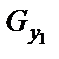 ,
, 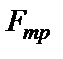 по-прежнему определяются также как в случае 1
по-прежнему определяются также как в случае 1
Учитывая, что 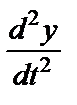 = 0, упрощаем первое из уравнений (34):
= 0, упрощаем первое из уравнений (34):
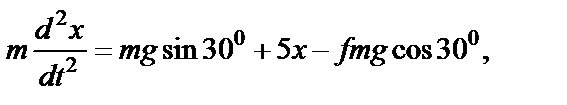
или
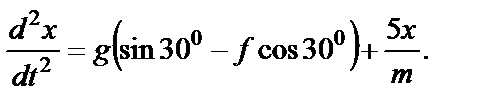
В числах:
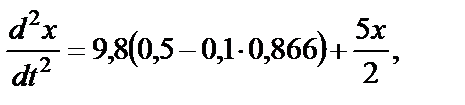
окончательно
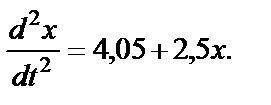
Запишем это уравнение так:
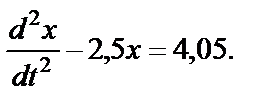 (35)
(35)
Введем обозначение: k2=2,5.
Уравнение (35) примет вид:
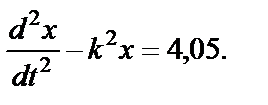
Согласно правилам математики, такое уравнение имеет решение в виде:
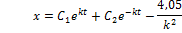
| (36) |
Постоянные 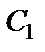 и
и 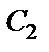 определяем по начальным условиям: при
определяем по начальным условиям: при 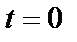
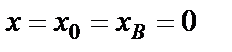 ;
; 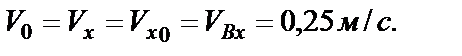
Для применения начальных условий находим уравнение скорости, продифференцировав по времени выражение (36)
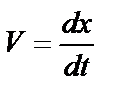
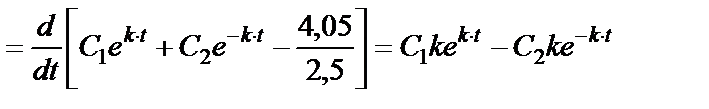 . (37)
. (37)
Введем в уравнения (36) и (37)указанные начальные условия и получим
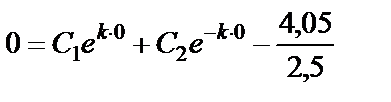 ,
,
и 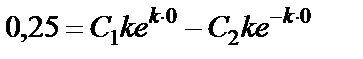 .
.
После преобразований имеем:
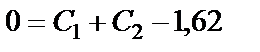 , (38)
, (38)
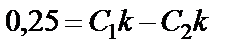 . (39)
. (39)
Из этих уравнений находим 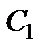 и
и 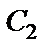
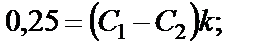
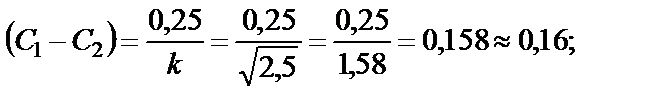
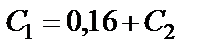 . (40)
. (40)
Подставим найденное для С1 выражение(40) в формулу (38):
0=0,16+С2+С2 –1,62, или 0=2С2 – 1,46,
откуда С2= 0,73.
Тогда численное значение С1 равно
С1=0,16 + 0,73=0,89.
Подставляя найденные значения 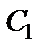 и
и 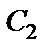 в уравнение (36), находим уравнение движения тела на участке ВС.
в уравнение (36), находим уравнение движения тела на участке ВС.
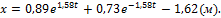
4. Случай, когда на участке ВС на тело действует сила 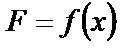 .
.
Допустим 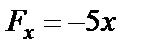 . Дифференциальные уравнения будут такие же, как и в предыдущем случае, с той лишь разницей, что
. Дифференциальные уравнения будут такие же, как и в предыдущем случае, с той лишь разницей, что 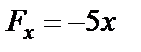 , а не
, а не 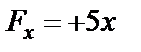 . Силу
. Силу 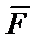 направим против движения.
направим против движения.
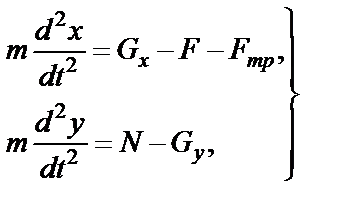 (41)
(41)
где силы 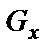 ,
, 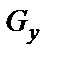 ,
, 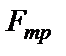 находятся, как указано выше.
находятся, как указано выше.
Делая замену как в предыдущем случае, получаем первое из уравнений (41) в следующем виде:
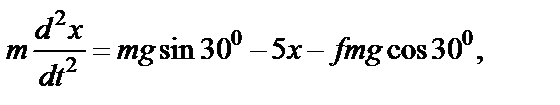
после преобразования:
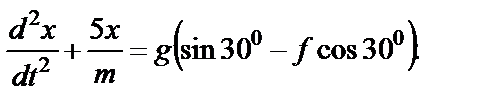
С учетом численных значений известных величин (напомним,
что m=2 кг)
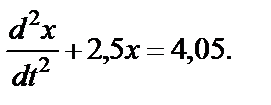 (42)
(42)
Введем обозначение k2=2,5, тогда выражение (42) примет вид
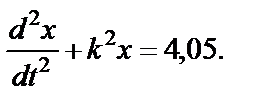
Согласно правилам математики, такое уравнение имеет решение в виде:
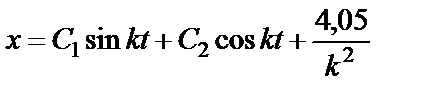 , (43)
, (43)
где 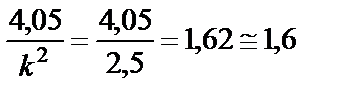 ;
;
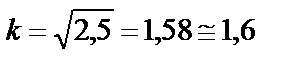 .
.
Тогда уравнение (43) запишется так
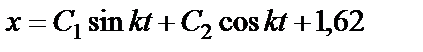 . (44)
. (44)
Чтобы применить начальные условия: при 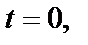
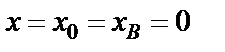 и
и 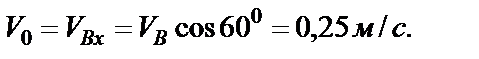 для определения постоянных
для определения постоянных 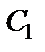 и
и 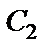 , находим уравнение скорости
, находим уравнение скорости
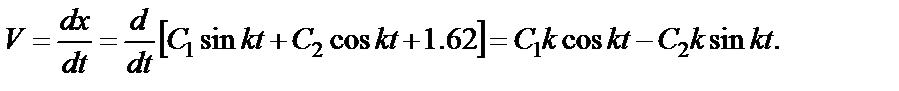 (45)
(45)
Подставляем в уравнения (44) и (45) указанные начальные условия
0=C1sink·0 + C2cosk·0 + 1,62,
0,25= C1 k cosk·0 - C2 k sink·0.
После преобразований эти выражения примут вид
0= C2+ 1,6,
0,25= C1 k
Откуда находим С1 и С2
C2=- 1,62,
C1=0,25/k=0,25/1,58 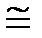 0,16,
0,16,
и, подставляя их значения в уравнение (44), получим уравнение движения тела на участке ВС.
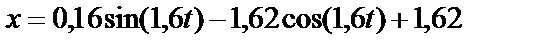 (м).
(м).
Динамика механической системы (твёрдого тела).
Существуют две меры инертности тела: масса и момент инерции.
Инертность – это свойство тела сопротивляться изменению своей скорости.
Масса m используется как мера инертности тела при его поступательном движении, а при вращательном движении мерой инертности является момент инерции JZ.
|
|
|
Момент инерции JZ относительно оси (Z) равен сумме произведений масс частиц тела на квадрат их расстояний до оси т.е.

|
и характеризует распределение массы в теле.
Для тяжёлого кольца (или маховика, у которого масса распределена по его ободу) массой m и радиусом R момент инерции его относительно оси, проходящей через его центр перпендикулярно плоскости кольца, равен
JZ=mR2
Для сплошного однородного диска (или цилиндра) массой m и радиусом R момент инерции его относительно центральной оси равен
JZ=mR2 /2.
Существуют две меры механического движения: количество движения и кинетическая энергия.
Количество движения используется, когда механическое движение не переходит в другие виды движения, а изменяется только по своим характеристикам, во всех остальных случаях в качестве меры используется кинетическая энергия.
Количество движения 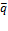 материальной точки равно
материальной точки равно 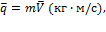
где 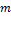 - масса точки,
- масса точки, 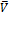 - её скорость.
- её скорость.
Кинетическая энергия материальной точки равна
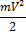
Кинетическая энергия Т механической системы равна сумме кинетических энергий тел, входящих в эту систему, т.е.

где n - количество тел в механической системе.
Кинетическая энергия тела определяется в зависимости от вида его движения по следующим формулам:
при поступательном движении

где 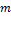 - масса тела, V - его скорость,
- масса тела, V - его скорость,
при вращательном движении

где 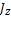 - момент инерции тела относительно оси вращения (оси Z),
- момент инерции тела относительно оси вращения (оси Z), 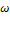 - угловая скорость вращения тела,
- угловая скорость вращения тела,
при плоскопараллельном движении
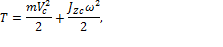
где 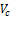 - скорость центра масс тела (точки С),
- скорость центра масс тела (точки С), 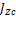 - момент инерции тела относительно мгновенной оси вращения, проходящей через центр масс тела (ось ZC).
- момент инерции тела относительно мгновенной оси вращения, проходящей через центр масс тела (ось ZC).
Совместно с кинетической энергией тела, как мера действия на него силы, используется её работа А.
Работа (А) постоянной силы ( ) на конечном перемещении (S) точки её приложения (точки М) равна
) на конечном перемещении (S) точки её приложения (точки М) равна
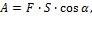
где α - угол между вектором силы и направлением перемещения или направлением скорости точки М (смотри рисунок 33).

Если сила переменная величина, то работа находится следующим образом
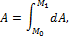
где 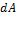 - элементарная работа силы, которую можно найти по формулам:
- элементарная работа силы, которую можно найти по формулам:
|
|
|
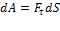
и
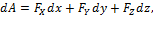
где 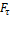 - проекция силы на направление перемещения точки М,
- проекция силы на направление перемещения точки М, 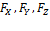 –проекции силы на координатные оси XYZ,
–проекции силы на координатные оси XYZ, 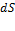 - элементарное перемещение точки М,
- элементарное перемещение точки М, 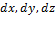 - проекции элементарного перемещения точки на координатные оси.
- проекции элементарного перемещения точки на координатные оси.
Наконец, работу некоторых сил можно вычислить с помощью следующих выражений:
для силы тяжести (G)
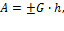
где  - перемещение центра масс тела по высоте, знак «+» - если тело опускается, «-» - если поднимается;
- перемещение центра масс тела по высоте, знак «+» - если тело опускается, «-» - если поднимается;
для силы упругости (F упр)
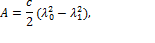
где  - коэффициент упругости,
- коэффициент упругости, 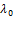 ,
, 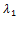 - начальная и конечная деформации пружины;
- начальная и конечная деформации пружины;
для момента силы (M)
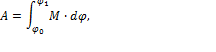
где 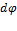 - элементарный угол поворота тела под действием момента М, φ 0, φ 1- начальное и конечное значения угла поворота тела.
- элементарный угол поворота тела под действием момента М, φ 0, φ 1- начальное и конечное значения угла поворота тела.
Для решения задач часто используется теорема об изменении кинетической энергии механической системы: изменение кинетической энергии (Т1- Т0) механической системы на конечном её перемещении равно сумме работ сил, приложенных к системе на этом перемещении, т.е.
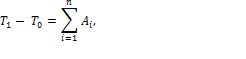
где 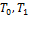 - начальная и конечная кинетические энергии механической системы.
- начальная и конечная кинетические энергии механической системы.
Задача 7 (Д2). Тема: Теорема об изменении кинетической энергии механической системы.
Задание: механическая система, изображённая на рисунке (смотри рисунки 7.0 - 7.9) в начальный момент времени в состоянии покоя, приводится в движение силой 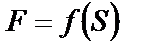 , зависящей от перемещения S точки её приложения. Деформация пружины в моментначала движения равна нулю. При движении механической системы на шкив 3 действует постоянный момент М С сил сопротивления.
, зависящей от перемещения S точки её приложения. Деформация пружины в моментначала движения равна нулю. При движении механической системы на шкив 3 действует постоянный момент М С сил сопротивления.
Определить значение искомой величины в тот момент, когда перемещение S станет равным S 1=0,4м. Скольжением пренебречь. При решении использовать следующие данные: радиусы ступенчатого шкива 3 R 1=0.3м, R 1= r 3=0,15м, его радиус инерции ρ 3=0,2м. Массу блока 4 считать равномерно распределённой по ободу, а тела 1 и 2 – сплошными однородными цилиндрами, коэффициент трения скольжения грузов 5 и 6 о плоскость f =0,1.
Другие данные, в том числе и жёсткость пружины с, указаны в таблице 7.
Таблица 7
| Ва- ри- ант | m 1, кг | m 2, кг | m 3, кг | m 4, кг | m 5, кг | m 6, кг | с, Н/м | М С, Нм | F = f (S),Н | На- йти |
| 1,4 | 50(4+6S) | VC1 | ||||||||
| 1,6 | 26(4+2S) | V6 | ||||||||
| 1,8 | 40(2+6S) | ω4 | ||||||||
| 2,0 | 80(4+6S) | ω3 | ||||||||
| 2,4 | 60(8+2S) | VC2 | ||||||||
| 1,2 | 30(4+5S) | ω1 | ||||||||
| 0,8 | 55(2+8S) | ω4 | ||||||||
| 0,6 | 45(1+4S) | V6 | ||||||||
| 1,2 | 50(4+6S) | V5 | ||||||||
| 2,1 | 36(2+3S) | ω3 |





План выполнения задания
При решении задачи учесть, что кинетическая энергия Т механической системы равна сумме кинетических энергий тех тел, входящих в систему, для которых дана масса. Кинетическую энергию этих тел надо вы-
разить через ту скорость (линейную или угловую), которую требуется определить в задаче. Затем определить работу внешних сил, действующих на механическую систему. При вычислении работы надо перемещения тел выразить через перемещение S 1 точки приложения силы 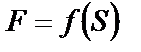 ,которое задано в задаче. Приравнивая изменение кинетической энергии механической системы к сумме работ внешних сил, определить искомую величину.
,которое задано в задаче. Приравнивая изменение кинетической энергии механической системы к сумме работ внешних сил, определить искомую величину.
Пример
Решить указанную в задании задачу при следующих данных:
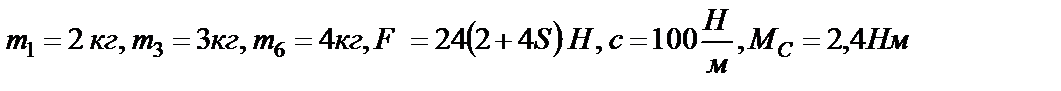 и
и
определить угловую скорость тела 1 (ω 1-?).
Решение

1. К решению задачи применяем теорему об изменении кинетической энергии неизменяемой механической системы
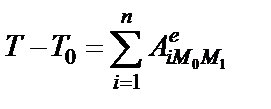 , (46)
, (46)
где Т 0 – кинетическая энергия механической системы, показанной на рисунке 1 в начальный момент времени в состоянии покоя (Т 0=0), Т - кине-
тическая энергия системы, соответствующая положению, когда точка С 5 приложения силы 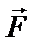 переместится на расстояние S = S 1.
переместится на расстояние S = S 1.
Получаем
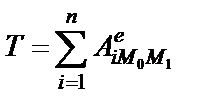
2. Определяем кинетическую энергию Т механической системы. Она состоит из кинетических энергий тел 1, 3, 6, для которых в задаче даны массы 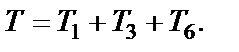 (47)
(47)
При движении механической системы тело 1 совершает плоское движение,
поэтому его кинетическую энергию находим по формуле
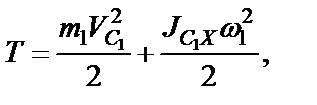 (48)
(48)
где m 1 – масса тела 1, 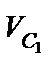 - скорость его центра масс (т. С 1),
- скорость его центра масс (т. С 1), 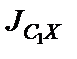 - момент инерции тела относительно оси X, проходящей через центр масс тела перпендикулярно плоскости рисунка (рис.34), ω 1 – угловая скорость относительного вращательного движения тела 1.
- момент инерции тела относительно оси X, проходящей через центр масс тела перпендикулярно плоскости рисунка (рис.34), ω 1 – угловая скорость относительного вращательного движения тела 1.
Шкив 3 вращается вокруг неподвижной оси (XC 3), его кинетическую энергию определяем формулой
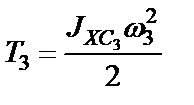 , (49)
, (49)
где 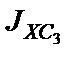 - момент инерции тела относительно оси его вращения, ω 3 - угловая скорость тела.
- момент инерции тела относительно оси его вращения, ω 3 - угловая скорость тела.
Тело 6 движется поступательно, его кинетическая энергия
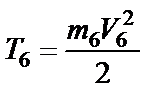 , (50)
, (50)
где m 6 – масса тела, V 6 – его скорость.
3. Устанавливаем связь между скоростями и перемещениями тел. Обращаем внимание, что в задаче требуется определить угловую скорость ω 1 тела 1 для того положения механической системы, когда S = S 1, поэтому скорости, входящие в формулы (48), (49), (50), выражаем через ω 1.
В точке Р касания тела 1(сплошного однородного цилиндра) с неподвижной плоскостью находится его мгновенный центр скоростей, поэтому
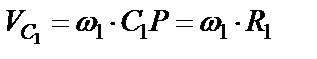 , (51)
, (51)
и 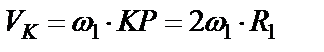
но VK = VD, значит
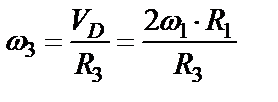 , (52)
, (52)
и 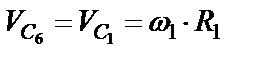
Кроме того, замечаем, что 
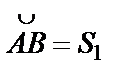 (смотри рис. 35), откуда угол поворота шкива 3 равен
(смотри рис. 35), откуда угол поворота шкива 3 равен

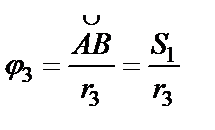 .
.
Перемещение точки D равно
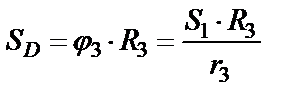 ,
,
так как VD = VK, то
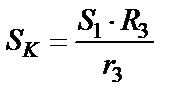 .
.
Учитывая, что 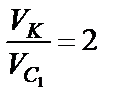 , получим
, получим
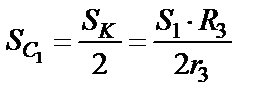
и 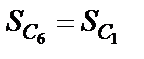 .
.
4. Определяем моменты инерции тел. В задаче предложено тело 1 считать сплошным однородным цилиндром, поэтому
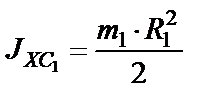 , (54)
, (54)
а для шкива 3 дан радиус инерции ρ 3 относительно оси вращения, тогда его момент инерции
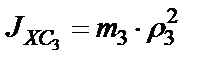 . (55)
. (55)
5. Находим кинетические энергии тел 1, 3, 6, делая подстановку в формулы (48), (49), (50) выражений (51), (52), (53), (54), (55). Получим
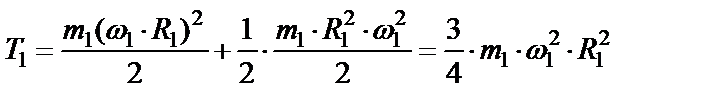 ,
,
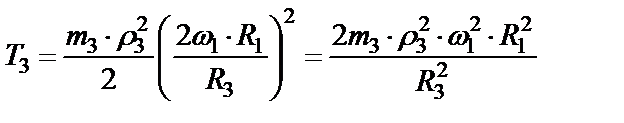 ,
,
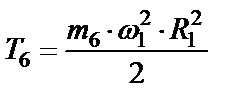 .
.
Вычисляем кинетическую энергию механической системы по формуле (47)
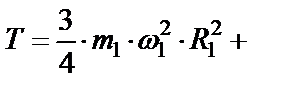
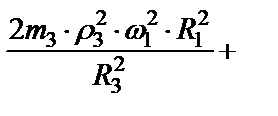
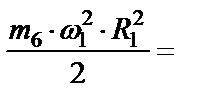
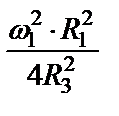 (
(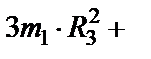
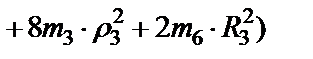 ,
,
или в числах
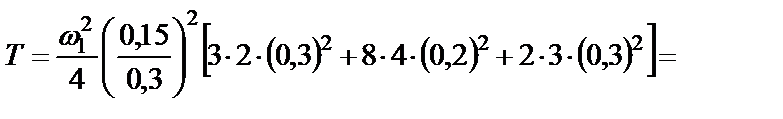
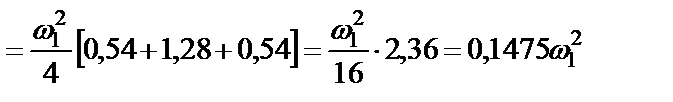 .
.
 6. Указываем внешние силы, приложенные к механической системе (смотри рис. 34):
6. Указываем внешние силы, приложенные к механической системе (смотри рис. 34): 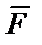 - заданная сила;
- заданная сила; 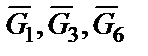 - силы тяжести тел 1, 3, 6;
- силы тяжести тел 1, 3, 6; 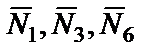 - реакции связей;
- реакции связей; 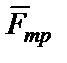 - сила трения;
- сила трения; 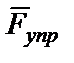 - сила упругости деформированной пружины. Определяем работы внешних сил на заданном перемещении S = S 1.
- сила упругости деформированной пружины. Определяем работы внешних сил на заданном перемещении S = S 1.
Работа переменной силы 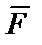
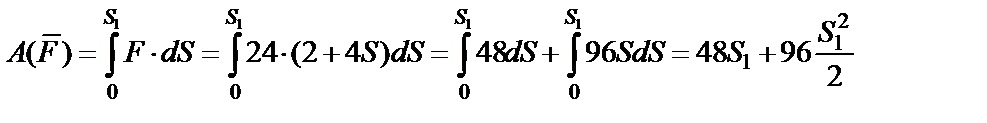 ,
,
или в числах
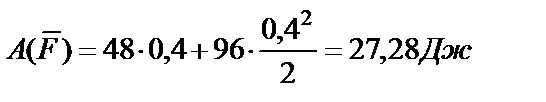 .
.
Работы сил 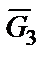 и
и 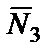 равны нулю, т.е.
равны нулю, т.е. 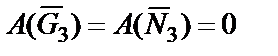 , так как силы приложены к неподвижной точке С 3.
, так как силы приложены к неподвижной точке С 3.
Работа момента сопротивления М С
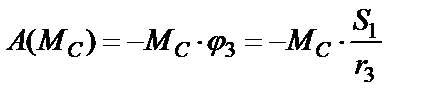 ,
,
в числах
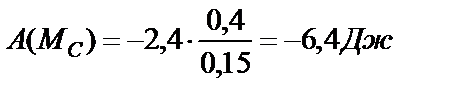 .
.
Работы сил 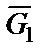 ,
, 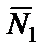 и
и 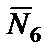 равны нулю, т.е.
равны нулю, т.е. 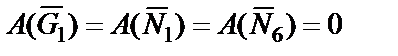 , так как точки приложения этих сил С 1 и С6 перемещается в направлении перпендикулярном силам.
, так как точки приложения этих сил С 1 и С6 перемещается в направлении перпендикулярном силам.
Работа силы 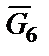
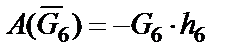 ,
,
где 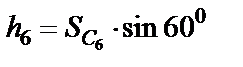 - перемещение по высоте точки С6 приложения силы
- перемещение по высоте точки С6 приложения силы 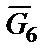 , тогда
, тогда
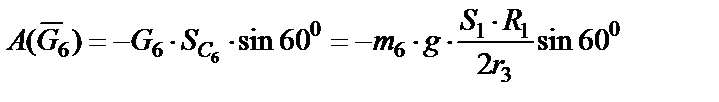 ,
,
в числах
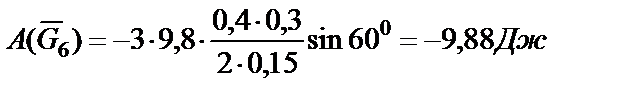 .
.
Работа силы 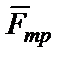 трения при движении тела 6
трения при движении тела 6
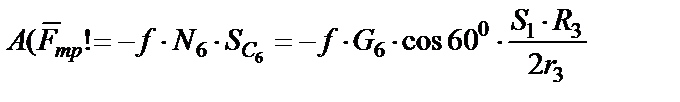 ,
,
в числах 
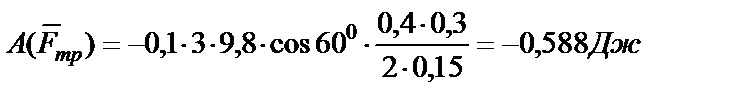 .
.
Работа силы 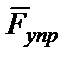 упругости растянутой пружины
упругости растянутой пружины
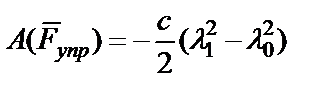 ,
,
где λ 0 – начальная деформация пружины (λ 0=0), λ 1 – конечная деформация пружины (λ 1= 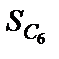 ). Тогда
). Тогда
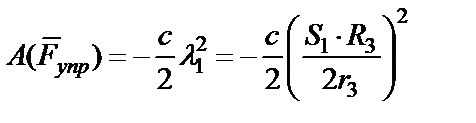 ,
,
или в числах 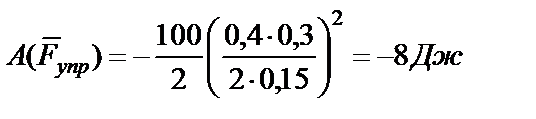 .
.
Определяем сумму работ внешних сил, приложенных к механической системе
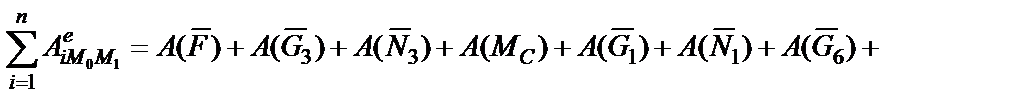
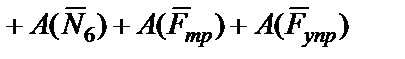 ,
,
или в числах
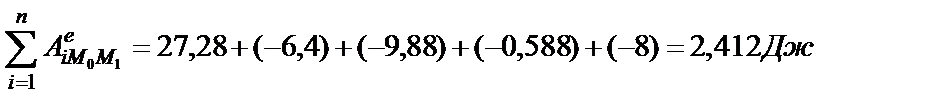 .
.
Подставляем найденные значения кинетической энергии Т 1 и суммы работ внешних сил 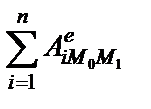 в выражение (46)
в выражение (46)
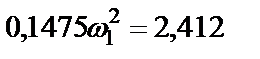 .
.
Откуда находим угловую скорость ω 1 относительного вращательного движения тела 1
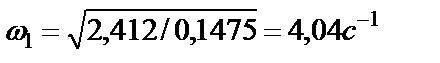 .
.
Аналитическая механика
Для механической системы, находящейся в равновесии, с целью определения неизвестных сил, приложенных к ней, удобно применять принцип возможных перемещений: для механической системы, находящейся в равновесии, сумма элементарных работ активных сил на любом возможном перемещении системы равна нулю, т.е.
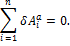
По этому принципу для механической системы составляется столько уравнений равновесия, сколько независимых возможных перемещений ей можно задать (или сколько степеней свободы она имеет). Степень свободы механической системы (механизма) можно определить с помощью простого правила: если у механической системы (механизма) остановить поступательное или вращательное движение одного тела, и она остановится, то степень свободы равна единице, если же часть системы продолжает двигаться, но после остановки поступательного или вращательного движения второго тела вся система остановится, то её степень свободы равна двум и так далее.
Для того, чтобы перемещение (δS) считалось возможным – оно должно быть очень малым (элементарным) и не должно нарушать наложенные на механическую систему связи.
Задача 8 (Д3). Тема: Принцип возможных перемещений.
Задание: дан шестизвенный механизм OABECD (смотри рисунки 8.0 – 8.9), длины звеньев которого известны: OA= l 1=0,35м, AC= l 2=1,4м, BO1= l 3=0,7м, CD= l 4=0,875м, AB=BC. Механизм находится в равновесии под действием двух пар с моментами М1 и М2 и силы упругости F упр
пружины, действующей на поршень 5 (коэффициент упругости с пружины задан в таблице 8).
Для положения механизма, заданного величинами углов α 1, α 2, β, γ, φ
(численные значения их приведены в таблице 8) определить величину деформации пружины и её вид (сжимается пружина или растягивается). Указанные углы устанавливаются по транспортиру, направление их откладывания показано на рисунках дуговыми стрелками. Вес звеньев не учитывать.
Таблица 8
| Ва- ри- ант | α 10 | α 20 | β 0 | γ 0 | φ 0 | с, Н/см | М1, Нм | М2, Нм |
| 120 | ||||||||
| 90 | ||||||||





Рассмотрим решение задачи на следующем примере. Механизм показан в произвольном масштабе на рисунке 36.
Дано: OA= l 1=0,35м, AC= l 2=1,4м, BO1= l 3=0,7м, CD= l 4=0,875м, AB=BC,
α 1=1200, α 2=1100, β =450, γ =800, φ =600, с =150Н/см, М1=150Нм, М2=300Нм.

1. Изображаем механизм в заданном по заданию положении в произвольном масштабе. Начинаем построение со звена 1 (ОА), а далее под углами β, γ, α 2, φ последовательно откладываем звенья 2, 3, 4 и ось направляющих ползуна 5.
2. Показываем все приложенные силовые факторы: моменты М1 и М2 и силу упругости пружины (F упр= с ∙λ), которую направляем, считая пружину растянутой.
3. Определяем степень свободы механизма, используя приведённое выше правило. Степень свободы равна единице, значит, надо составить только одно уравнение равновесия вида
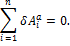
4.Задаём механизму независимое возможное перемещение (δφ 1 для звена 1) по направлению действия момента М1. Звенья 1 и 3 могут совершать
вращательное движение относительно стойки 6, звенья 2 и 4 – плоское движение, звено 5 – поступательное движение. Положение механизма, вызванное возможным перемещением δφ 1, показано на рисунке 30 пунктирными линиями.
5. Составляем уравнение равновесия механизма
М1 δφ 1 – М2 δφ 2 + F упр δS D=0
6. Независимое возможное перемещение только одно - δφ 1 (так как количество независимых возможных перемещений равно степени свободы механизма). Выразим возможные перемещения δφ 2, δS D через δφ 1. Для этого используем возможные скорости точек A, B, C, D (V A, V B, V C, V D).
Из формулы 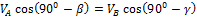
Учитывая, что 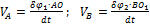
получим 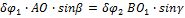
откуда
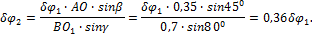
Для определения зависимости 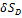 от
от 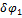 найдем угол
найдем угол 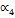 .
.
Для этого рассмотрим выражение
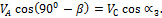 (47)
(47)
Скорость 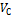 найдем используя мгновенный центр скоростей звена 2 (точка
найдем используя мгновенный центр скоростей звена 2 (точка 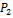 )
)
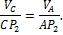
Отрезок 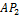 найдем из треугольника
найдем из треугольника 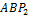 по теореме синусов
по теореме синусов
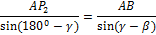
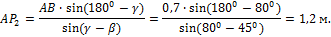
Отрезок 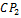 найдем из треугольника
найдем из треугольника 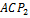 по теореме косинусов
по теореме косинусов
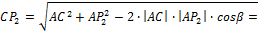
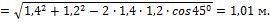
Тогда
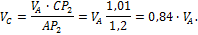
Подставив значение 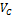 в выражение (47)
в выражение (47)
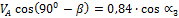
откуда 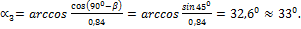
Из выражения
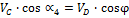
с учетом 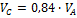
найдем
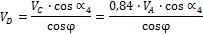
и переходя к возможным перемещениям и учитывая, что 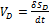 получим
получим
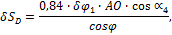
где 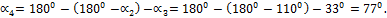
В результате имеем
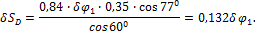
После подстановки значений 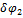 и
и 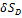 через
через 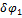 в уравнение равновесия оно примет вид
в уравнение равновесия оно примет вид
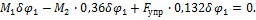
Откуда находим 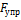
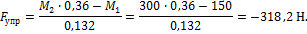
Знак “-” говорит о том, что пружина не растягивается, как предполагалось, а сжимается. Найдем деформацию пружины 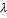
 2015-03-20
2015-03-20 351
351







