Описание распространения колебаний в упругой среде
Каждое тело обладает в той или иной степени способностью восстанавливать свою форму, измененную в результате кратковременного действия сил. Рассмотрим процессы, возникающие в упругой среде под действием периодической силы. Пусть источником периодической силы является колеблющееся тело. Частицы среды, непосредственно прилегающие к телу, также будут участвовать в колебательном движении. В результате упругого взаимодействия их с соседними частицами последние также начнут колебаться. Таким образом, колебания будут передаваться от одних точек к другим с конечной скоростью. Упругостью сжатия и растяжения обладают все тела: твердые, жидкие и газообразные, поэтому колебания могут распространяться в любых телах. Процесс распространения колебаний в какой-либо среде называется волной. В результате распространения волны частицы будут совершать колебания около положения равновесия. При этом происходит передача энергии без переноса вещества.Если колебания частиц происходят в том же направлении, что ираспространение энергии, то такие волны называются продольными. Если же колебания частиц перпендикулярны к направлению распространения энергии, то такие волны называются поперечными. Примером продольных волн могут служить волны, возникающие в металлическом стержне в результате деформации сжатия и растяжения при ударе молотком в торец стержня. Вообще же продольные волны характерны для жидких и газообразных сред. Волны, возникающие при колебаниях струны, являются поперечными, так как смещение отдельных элементов струны перпендикулярно направлению распространения колебаний. Поперечные волны обусловлены деформациями сдвига. В твердых телах могут распространяться как продольные, так и поперечные волны. В жидкостях и газах деформации сдвига не являются упругими, т. е. сдвинутые друг относительно друга слои жидкости не стремятся вернуться в исходное положение (волны на поверхности жидкости не являются, строго говоря, поперечными, а носят более сложный характер). Поэтому в жидкостях и газах могут распространяться только продольные волны. Поперечные и продольные волны описываются подобными уравнениями.
|
|
|
Уравнение бегущей волны
Рассмотрим процесс распространения колебания, источником которого является точка О (рис. 1), колеблющаяся гармонически по закону:
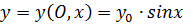 . (1)
. (1)
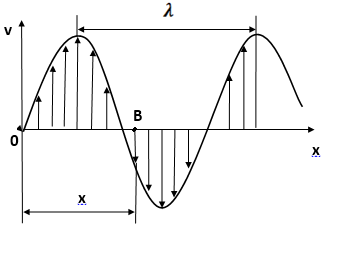
Рис. 1. Бегущая волна
Пусть колебание точки началось в момент времени  . Соседние точки придут в колебание с той же амплитудой
. Соседние точки придут в колебание с той же амплитудой  и частотой
и частотой 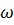 , что и точка O, но с некоторым запаздыванием. Начало колебаний точки В, отстоящей на расстоянии x от источника, отстанет от начала колебаний точки О на время
, что и точка O, но с некоторым запаздыванием. Начало колебаний точки В, отстоящей на расстоянии x от источника, отстанет от начала колебаний точки О на время
|
|
|
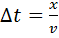 , (2)
, (2)
где 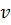 — скорость волны в данной среде.
— скорость волны в данной среде.
Если величина отклонения точки О от положения равновесия в момент времени 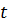 равна
равна 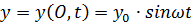 , вследствие запаздывания отклонение точки В в тот же момент времени
, вследствие запаздывания отклонение точки В в тот же момент времени 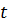 будет таким же, каким было отклонение точки О на время
будет таким же, каким было отклонение точки О на время 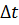 ранее, т. е.
ранее, т. е.
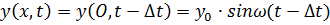 , (3)
, (3)
или
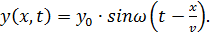 (4)
(4)
Уравнение (4) называется уравнением бегущей волны.
Таким образом, из уравнения (4) следует, что смещение произвольной точки зависит от двух переменных - расстояния 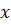 от точки до источника и времени наблюдения
от точки до источника и времени наблюдения 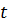 .
.
Расстояние, на которое распространяется колебание за один период, называется длиной волны 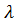 :
:
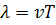 , (5)
, (5)
Где Т - период колебаний. Так как 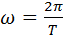 , то уравнение бегущей волны можно переписать в виде:
, то уравнение бегущей волны можно переписать в виде:
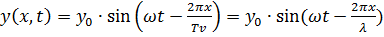 . (6)
. (6)
Из сопоставления последнего выражения с уравнением (2) видно, что колебание точки с координатой 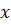 сдвинуто по фазе относительно колебаний в точке O на величину
сдвинуто по фазе относительно колебаний в точке O на величину 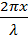 .
.
Определим фазу 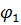 колебаний в точке, отстоящей от точки с координатой
колебаний в точке, отстоящей от точки с координатой 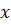 на расстоянии, равном длине волны
на расстоянии, равном длине волны 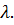 Фаза точки с координатой
Фаза точки с координатой 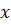 равна:
равна:
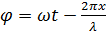 , (7)
, (7)
тогда
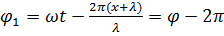 , (8)
, (8)
т. е. фазы точек с координатами 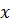 и
и 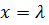 совпадают. Поэтому длину волны можно определить как расстояние между ближайшими двумя точками, колеблющимися в одинаковых фазах (рис. 1). Скорость распространения колебаний можно представить в виде:
совпадают. Поэтому длину волны можно определить как расстояние между ближайшими двумя точками, колеблющимися в одинаковых фазах (рис. 1). Скорость распространения колебаний можно представить в виде:
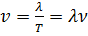 , (9)
, (9)
где 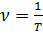 - частота колебания.
- частота колебания.
На рис. 2 изображены положения точек образующейся волны для шести последовательных моментов времени через четверть периода. Из формулы (9) видно, что скорость распространения колебаний (например, звуковых) можно определить, зная частоту источника 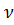 и длину волны
и длину волны 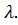 Частота
Частота 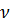 задается источником колебаний (в случае звуковых волн - камертоном, звуковым генератором). Длина волны
задается источником колебаний (в случае звуковых волн - камертоном, звуковым генератором). Длина волны 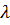 может быть определена методом интерференции.
может быть определена методом интерференции.
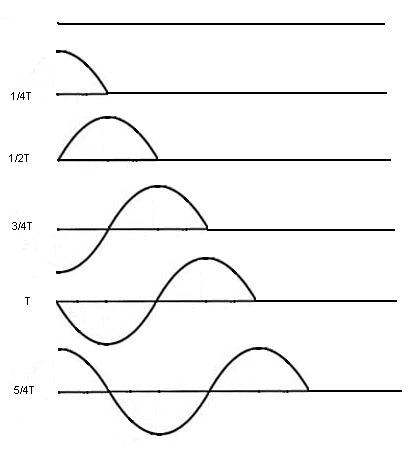
Рис. 2. Распространение волны.
Явление интерференции
Источники волн, колеблющиеся с одинаковой частотой и постоянной разностью фаз, называются когерентными. Волны, излучаемые когерентными источниками, также одинаковы по частоте и имеют ту же постоянную разность фаз. В результате наложения (суперпозиции) когерентных волн наблюдается явление, называемое интерференцией. Оно заключается в том, что в одних местах пространства происходит усиление волнового движения, а в других - ослабление или полное погашение его. На практике когерентные волны можно получить от одного источника. Для этого поток энергии, излучаемый источником, разделяется на две части. Образующиеся две волны направляют по путям различной длины, а затем соединяют, в результате чего волны интерферируют друг с другом.
Рассмотрим явление интерференции на примере распространения звуковых волн от одного источника A, по трубам 1и 2 (рис. 3). Пусть длина пути по трубе 1 до произвольной точки С равна 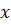 , а по трубе 2 -
, а по трубе 2 - 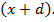
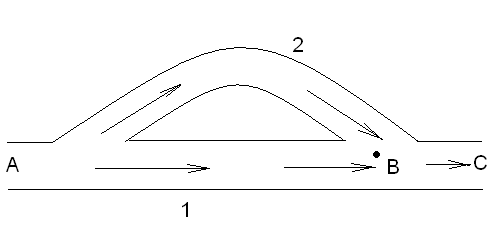
Рис. 3. Устройство для получения интерференции.
Очевидно, правее точки В обе волны распространяются с постоянной разностью хода, равной d. Запишем уравнения волн 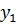 и
и 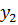 , выходящих из труб 1 и 2:
, выходящих из труб 1 и 2:
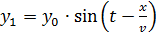 , (10)
, (10)
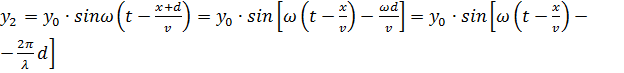 . (11)
. (11)
Из сопоставления уравнений (10) и (11) видно, что постоянная разность хода d приводит к постоянной разности фаз 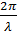 d. Результирующее колебание в точке С будет равно сумме колебаний
d. Результирующее колебание в точке С будет равно сумме колебаний 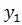 и
и 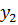 :
:
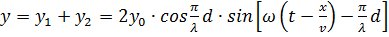 . (12)
. (12)
Последнее уравнение описывает бегущую волну, амплитуда которой равна 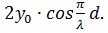 Если
Если 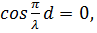 то амплитуда колебаний равна нулю, т.е. волны полностью гасят друг друга (если амплитуды колебаний
то амплитуда колебаний равна нулю, т.е. волны полностью гасят друг друга (если амплитуды колебаний 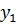 и
и 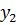 несколько различны, то в таких случаях получается минимум колебаний). Очевидно, условие минимумов имеет вид:
несколько различны, то в таких случаях получается минимум колебаний). Очевидно, условие минимумов имеет вид:
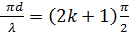 , (13)
, (13)
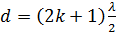 , (14)
, (14)
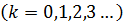 .
.
Таким образом, минимум амплитуды результирующего колебания получается тогда, когда вторая труба длиннее первой на нечетное число полуволн.
Максимум амплитуды результирующего колебания имеет место, если вторая труба длиннее первой на чётное число полуволн, т.е.
|
|
|
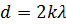 , (15)
, (15)
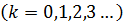 .
.
Пусть разность хода 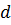 можно изменять, выполнив одну из труб вU-образной форме и подвижной. При этом расстояние, которому соответствует перемещение подвижной трубыпри переходе от одного минимума звучания ксоседнему, равняется
можно изменять, выполнив одну из труб вU-образной форме и подвижной. При этом расстояние, которому соответствует перемещение подвижной трубыпри переходе от одного минимума звучания ксоседнему, равняется 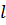 . Тогда для первого минимума (см. формулу (5))
. Тогда для первого минимума (см. формулу (5))
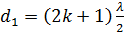 , (16)
, (16)
а для следующего минимума
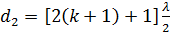 . (17)
. (17)
Так как при перемещении подвижной трубына величину 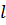 длина пути для звуковой волны по этой трубе увеличивается на 2
длина пути для звуковой волны по этой трубе увеличивается на 2 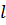 , то
, то 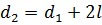 , откуда
, откуда
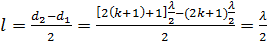 , (18)
, (18)
Следовательно:
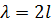 . (19)
. (19)
Подставляя значение 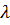 (19) в формулу (9), получим выражение, используемое для вычисления скорости звука в воздухе:
(19) в формулу (9), получим выражение, используемое для вычисления скорости звука в воздухе:
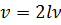 . (20)
. (20)
 2015-03-20
2015-03-20 1106
1106








