Если 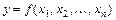 - дифференцируемая функция переменных
- дифференцируемая функция переменных 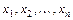 , являющихся дифференцируемыми функциями независимой переменной
, являющихся дифференцируемыми функциями независимой переменной 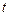 :
: 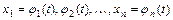 , то производная сложной функции
, то производная сложной функции 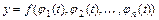 вычисляется по формуле
вычисляется по формуле 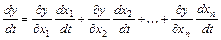 . Если
. Если 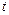 совпадает с одним из аргументов, например
совпадает с одним из аргументов, например 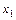 , то производная
, то производная 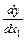 , называемая «полной» производной функции
, называемая «полной» производной функции 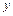 по
по 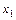 , вычисляется по формуле
, вычисляется по формуле
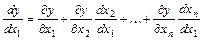 .
.
Если 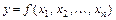 - дифференцируемая функция переменных
- дифференцируемая функция переменных 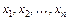 , являющихся дифференцируемыми функциями независимыx переменных
, являющихся дифференцируемыми функциями независимыx переменных 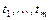 :
: 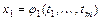 ,…,
,…, 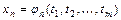 , то частные производные сложной функции
, то частные производные сложной функции 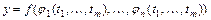 вычисляются по формулам:
вычисляются по формулам:
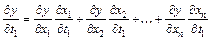 ,
,
………………………….………………..,
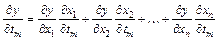 .
.
В частности, для функции 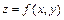 справедливы формулы:
справедливы формулы:
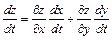 , где
, где 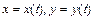 ;
;
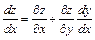 , где
, где 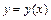 ;
;
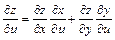 ,
, 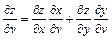 , где
, где 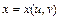 ,
, 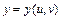 .
.
6.56 Найти 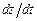 если
если
а) 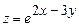 , где
, где 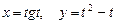 ;
;
б) 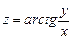 , где
, где 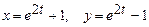 ;
;
в) 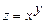 , где
, где 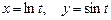 ;
;
г) 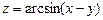 , где
, где 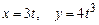 .
.
6.57 Найти 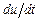 , если
, если
а ) 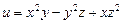 , где
, где 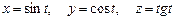 ;
;
б ) 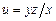 , где
, где 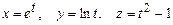 .
.
6.58 Найти 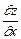 и
и 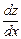 , если
, если
а) 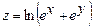 , где
, где 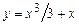 ;
;
б) 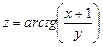 , где
, где 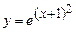 ;
;
в) 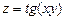 , где
, где 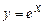 ; г)
; г) 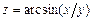 , где
, где 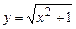 .
.
6.59 Найти 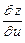 и
и 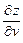 , если
, если
а) 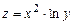 , где
, где 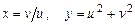 ;
;
б) 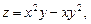 где
где 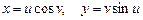 .
.
6.60 Найти 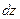 , если
, если
а) 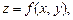 где
где 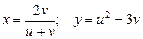 ;
;
б) 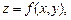 где
где 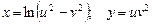 .
.
6.61 Показать, что следующие функции удовлетворяют данным уравнениям: а) 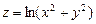 ,
, 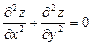 ;
;
б) 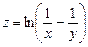 ,
, 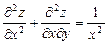 ;
;
в) 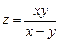 ,
, 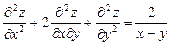 ;
;
г) 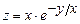 ,
, 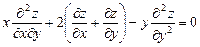 .
.
6.62 Предполагая, что произвольная функция  дифференцируема достаточное число раз, проверить следующие равенства:
дифференцируема достаточное число раз, проверить следующие равенства:
|
|
|
а) 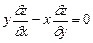 , если
, если 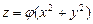 ;
;
б) 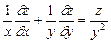 , если
, если 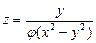 ;
;
в) 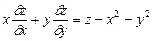 , если
, если 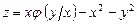 ;
;
г) 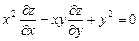 , если
, если 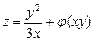 .
.
Если уравнение 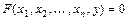 , где
, где 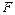 - дифференцируемая функция по переменным
- дифференцируемая функция по переменным 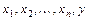 , определяет
, определяет 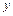 как функцию независимых переменных
как функцию независимых переменных 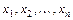 , то частные производные этой неявной функции
, то частные производные этой неявной функции 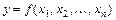 вычисляются по формулам:
вычисляются по формулам: 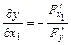 ,
, 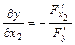 ,…,
,…, 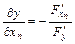 при условии, что
при условии, что 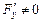 .
.
В частности, для функции 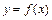 , заданной неявно уравнением
, заданной неявно уравнением 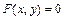 справедлива формула
справедлива формула 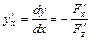 , при условии
, при условии 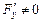 , а для функции
, а для функции 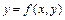 , заданной уравнением
, заданной уравнением 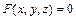
справедливы формулы: 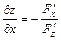 ,
, 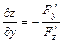 , при условии
, при условии 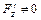 .
.
Частные производные высших порядков вычисляются последовательным дифференцированием данных формул.
6.63 Найти производную 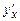 для функций
для функций 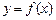 , заданных неявно:
, заданных неявно:
а) 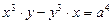 ; б)
; б) 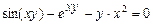 ;
;
в) 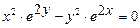 ; г)
; г) 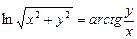 ;
;
д) 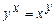
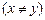 ; е)
; е) 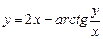 .
.
6.64 Найти производные указанного порядка для функций 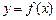 , заданных неявно:
, заданных неявно:
а) 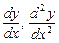 если
если 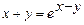 ;
;
б) 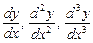 если
если 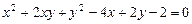 .
.
6.65 Найти частные производные 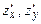 для функций
для функций 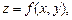 заданных неявно:
заданных неявно:
а) 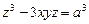 ; б)
; б) 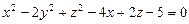 ;
;
в) 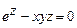 ; г)
; г) 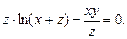
6.66 Найти дифференциал 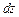 функции
функции 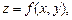 заданной неявно в указанной точке
заданной неявно в указанной точке 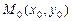 , если:
, если:
а) 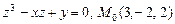 ; б)
; б) 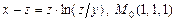 .
.
6.67 Найти дифференциал 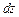 и производную
и производную 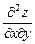 функции
функции 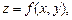 заданной неявно, если:
заданной неявно, если:
а) 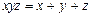 ; б)
; б) 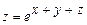 ;
;
в) 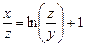 ; г)
; г) 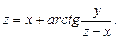
Если 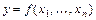 - дифференцируемая функция переменных
- дифференцируемая функция переменных 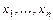 , то производная по направлению вектора
, то производная по направлению вектора 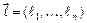 в точке
в точке 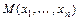 вычисляется по формуле
вычисляется по формуле 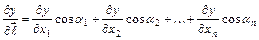 , где
, где 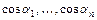 - координаты единичного вектора
- координаты единичного вектора 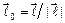 ,
, 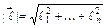 .
.
Градиентом дифференцируемой функции 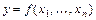 называется вектор
называется вектор 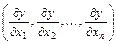 и обозначается
и обозначается 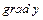 .
.
Скорость наибольшего изменения функции 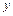 по направлению
по направлению 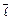 в точке
в точке 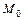 достигает наибольшего значения, если направление
достигает наибольшего значения, если направление 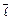 совпадает с направлением
совпадает с направлением 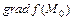 , т.е.
, т.е. 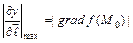 .
.
В частности, для функции 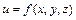 производная по направлению и градиент, вычисляются по формулам:
производная по направлению и градиент, вычисляются по формулам: 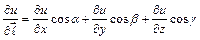 ,
, 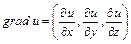 , где
, где 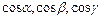 - направляющие косинусы вектора
- направляющие косинусы вектора 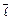 .
.
6.68 Найти производную 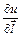 по направлению вектора
по направлению вектора 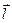 , градиент
, градиент 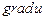 и его величину |
и его величину | 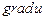 | в заданной точке
| в заданной точке 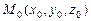 для следующих функций:
для следующих функций:
|
|
|
а) 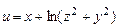 ,
, 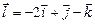 ,
, 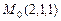 ;
;
б) 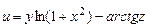 ,
, 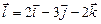 ,
, 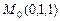 ;
;
в) 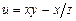 ,
, 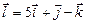 ,
, 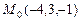 ;
;
г) 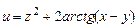 ,
, 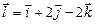 ,
, 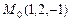 .
.
6.69 Найти угол между градиентами функции 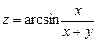 в точках
в точках 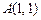 и
и 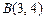 .
.
6.70 Найти угол между градиентами функций 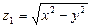 и
и 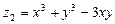 в точке
в точке 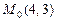 .
.
6.71 Найти 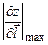 в точке
в точке 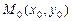 , если:
, если:
а) 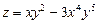 ,
, 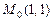 ; б)
; б) 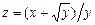 ,
, 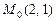 .
.
§5. Некоторые приложения частных производных.
Уравнение касательной плоскости к поверхности 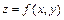 в точке
в точке 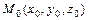 имеет вид
имеет вид
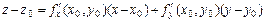 ,
,
а уравнение нормали – вид 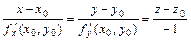 .
.
В случае задания поверхности неявным уравнением 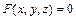 :
: 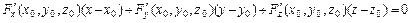 - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке 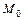 и
и
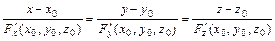 - уравнение нормали.
- уравнение нормали.
6.72 Написать уравнения касательной плоскости и нормали в точке 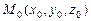 к следующим поверхностям:
к следующим поверхностям:
а) 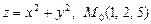 ; б)
; б) 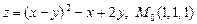 ;
;
в) 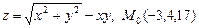 ;
;
г) 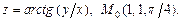
6.73 Написать уравнения касательной плоскости и нормали в точке 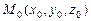 к следующим поверхностям:
к следующим поверхностям:
а) 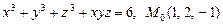 ;
;
б) 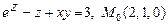 ; в)
; в) 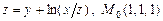 ;
;
г) 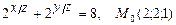 .
.
6.74 Для поверхности 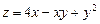 найти уравнение касательной плоскости, параллельной плоскости
найти уравнение касательной плоскости, параллельной плоскости 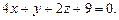
6.75 Для поверхности 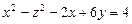 найти уравнение нормали, параллельной прямой
найти уравнение нормали, параллельной прямой 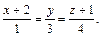
Множество точек 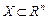 называется выпуклым, если вместе с любыми двумя своими точками
называется выпуклым, если вместе с любыми двумя своими точками 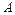 и
и 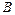 , оно содержит и отрезок
, оно содержит и отрезок 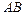 .
.
Функция 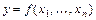 , определённая на выпуклом множестве
, определённая на выпуклом множестве 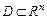 называется выпуклой вверх, если для всех точек
называется выпуклой вверх, если для всех точек 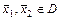 , где
, где 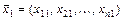 ,
, 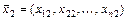 и для любого
и для любого 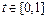 выполняется неравенство
выполняется неравенство 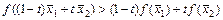 и выпуклой вниз, если
и выпуклой вниз, если 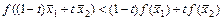 .
.
Матрица 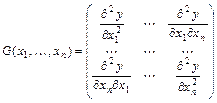 называется матрицей Гессе функции
называется матрицей Гессе функции 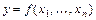 в точке
в точке 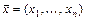 .
.
Дважды дифференцируемая на выпуклом множестве 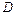 функция
функция 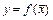 является на этом множестве: 1) выпуклой вниз, если
является на этом множестве: 1) выпуклой вниз, если 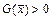 при всех
при всех 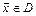 ; 2) выпуклой вверх, если
; 2) выпуклой вверх, если 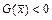 при всех
при всех 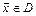 . Если на множестве
. Если на множестве 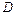 матрица Гессе
матрица Гессе 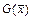 функции
функции 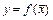 знакопеременна, то
знакопеременна, то 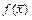 на этом множестве выпуклой не является.
на этом множестве выпуклой не является.
Знакоопределённость матрицы Гессе устанавливают, используя критерий Сильвестра знакоопределённости матриц квадратичных форм.
6.76. Исследовать следующие функции на выпуклость:
а) 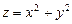 ; б)
; б) 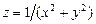 ;
;
в) 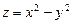 ; г)
; г) 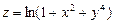 .
.
Частные эластичности функции 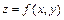 вычисляются по формулам:
вычисляются по формулам: 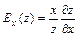 ,
, 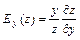 . Частные эластичности
. Частные эластичности 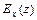 ,
, 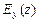 являются мерами реагирования переменной
являются мерами реагирования переменной 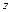 на изменение переменных
на изменение переменных 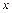 и
и 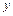 , и показывают приближённый процентный прирост
, и показывают приближённый процентный прирост 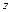 при изменении
при изменении 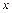 и
и 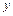 на один процент, соответственно.
на один процент, соответственно.
Под производственной функцией понимается функция 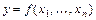 , независимые переменные которой
, независимые переменные которой 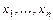 имеют смысл объёмов используемых ресурсов, а зависимая переменная
имеют смысл объёмов используемых ресурсов, а зависимая переменная 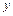 – объёма выпускаемой продукции.
– объёма выпускаемой продукции.
Предельной по переменной 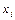 для
для 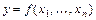 называется величина
называется величина 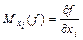 , средней – величина
, средней – величина 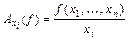 . Буква
. Буква 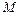 - сокращение от слова
- сокращение от слова 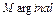 (предельный), буква
(предельный), буква 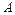 - сокращение от слова
- сокращение от слова 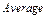 (средний).
(средний).
Производственной функцией Кобба-Дугласа называется функция вида 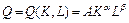 , где
, где 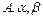 - некоторые постоянные,
- некоторые постоянные, 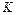 - объём производственных фондов,
- объём производственных фондов, 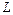 - объём трудовых ресурсов,
- объём трудовых ресурсов, 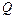 - объём выпускаемой продукции.
- объём выпускаемой продукции.
6.77. Найти частные эластичности 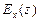 и
и 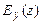 функций
функций 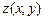 в указанных точках
в указанных точках 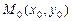 :
:
а) 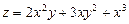 ,
, 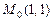 ; б)
; б) 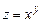 ,
, 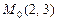 .
.
6.78 Для заданных значений 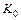 и
и 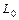 найти: а) среднюю и предельную производительности труда; б) среднюю и предельную фондоотдачу; в) эластичности выпуска по труду и по фондам, если производственная функция Кобба-Дугласа имеет вид:
найти: а) среднюю и предельную производительности труда; б) среднюю и предельную фондоотдачу; в) эластичности выпуска по труду и по фондам, если производственная функция Кобба-Дугласа имеет вид:
1) 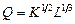 ,
, 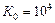 ,
, 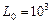 ;
;
2) 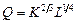 ,
, 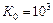 ,
, 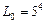 .
.
 2015-03-20
2015-03-20 659
659








