Множества

(С использованием материалов из Википедии)

Нынешние курсы математического анализа часто стро­ятся на понятии множества. Например, в учебнике Ю. Г. Решетняк «Курс математического анализа», с. 12:

«Для нас множество будет одним из первичных математических понятий, не выражаемым через другие математические понятия. Обычно, говоря слово,,множество‘‘, мы будем под этим понимать совокупность объектов произвольного рода, рассматриваемую как единое целое. Вместе с термином множество будут употребляться и его синонимы типа набор, система, совокупность и т. п. Напри­мер, можно говорить о множестве решений некоторого уравнения, о коллекции картин, хранящихся в музее, совокупности точек круга и т. д.

Объекты, составляющие то или иное множество, называются его элементами.

Множество считается заданным, если для любого объекта мож­но установить, является он элементом данного множества или нет».

В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов, «Ма­тематический анализ», с. 69:

«...при изучении вещественных чисел важным понятием явля­лось понятие множества. Подчеркнем, что множество мы рассмат­ривали как начальное понятие, неопределенное через другие.

В этом параграфе мы будем изучать множества произвольной природы или, как говорят, абстрактные множества. Это означает, что объекты, составляющие данное множество, или, как говорят, элементы данного множества уже не обязаны быть обязательно ве­щественными числами. Элементами абстрактного множества могут быть, например, функции, буквы алфавита, фигуры на плоскости и т. д.».

В. А. Зорич «Математический анализ»:

«Основные предпосылки канторовской (или, как условно гово­рят, "наивной") теории множеств сводятся к следующему:

1° множество может состоять из любых различных объектов; 2° множество однозначно определяется набором составляющих его объектов;

3° любое свойство определяет множество тех объектов, которые этим свойством обладают.

Если x — объект, P — свойство, P(x) — обозначение того, что x обладает свойством P, то через { x: P(x)} обозначают весь класс объектов, обладающих свойством P.

Объекты, составляющие класс или множество, называют эле­ментами класса или множества.

Слова "класс", "семейство", "совокупность", "набор" в наивной теории множеств употребляют как синонимы термина "множество". Следующие примеры демонстрируют применение этой термино­логии: множество букв "а" в слове "я"; множество жен Адама; набор из десяти цифр; семейство бобовых; множество песчинок на Земле; совокупность точек плоскости, равноудаленных от двух данных ее точек; семейство множеств; множество всех множеств.

Различие в степени определенности задания множеств наводит на мысль, что множество — не такое уж простое и безобидное поня­тие. И в самом деле, например, понятие множества всех множеств просто противоречиво.

Объедине́ние мно́жеств (тж. су́мма или соедине́ние) в теории множеств — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств 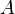и 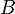обычно обозначается 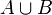, но иногда можно встретить запись в виде суммы .

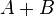Аксиома III (аксиома множества-суммы или объединения) Для любого множества а, содержащего по крайней мере один член, существует вполне определенное множество, членами которого являются в точности члены членов множества а.

Это множество называется множеством-суммой (sum-set) множества а, или объединением (union) членов а. Оно обозначается через «∪ а».
Итак, х ∈ ∪ а оказывается верным, в том и только в том случае, если найдется такое z ∈ a (по крайней мере одно z), что х ∈ z.

Грубо говоря, если множество а содержит члены t, u, v,..., то в ∪ а содержатся как раз члены множеств t, u, v,...; иногда мы будем поэтому обозначать множество-сумму множества а через t ∪ u ∪ v ∪..., где порядок членов не играет роли.

По правилам стандартной арифметики деление на число 0 запрещено.

Другое дело — деление на бесконечно малую функцию или последовательность, все члены которой отличны от нуля. При этом, в точках, в которых значение функции-делителя равно нулю, значение функции-частного не определено. Деление ограниченных отделённых от нуля функций на бесконечно малые приводит к появлению бесконечно больших, а отношение двух бесконечно малых называется неопределённостью 0/0, которую можно преобразовать (см. раскрытие неопределённостей) с тем, чтобы получить определённый результат.

Частное от деления какого-либо числа, отличного от нуля, на нуль не существует, так как в этом случае никакое число не может удовлетворять определению частного^[1].

Операции деления ненулевого числа на нуль не соответствует никакое действительное число. Однако число, отличное от нуля, можно разделить на число, как угодно близкое к нулю, и чем ближе делитель к нулю, тем больше будет частное. Поэтому, часто говорят, что результат этой операции считается «бесконечно большим» или «равным бесконечности» (положительной или отрицательной, в зависимости от знака операндов) и пишут:
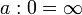, где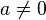
Смысл этого выражения состоит в том, что если делитель приближается к нулю, но не равен ему, а делимое остается равным a или приближается к нему, то частное неограниченно увеличивается (по модулю).

· Что такое 0? Прежде всего - это число. Далее. Это пустое множество, в котором нет элементов. Внимание. Это не отсутсвие множества, а отсутствие элементов во множесте. Само множество есть. неопределённость - это стационарное бесконечное множество нулей. Таким образом 0 (как число) разделяет бесконечность и неопределённость. Деление на ноль невозможно в пространстве комплексных чисел. В самом деле, если обозначить 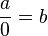, то по определению деления формально должно быть 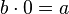, в то время как выражение 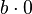, при любом комплексном 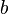, равно нулю. Другими словами, для нуля не существует обратного числа в пространстве комплексных чисел. Но это возможно нарасширенной комплексной плоскости.

В математическом анализе возможно 7 неопределенных ситуаций, в 4 из которых формально присутствует ноль (он обозначаетбесконечно малую величину):

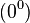
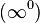
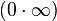
И вполне определенная ситуация, когда рассматривается предел бесконечно малой величины (справа или слева):

· Правый предел: 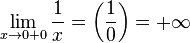_ или _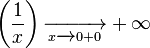

· Левый предел: 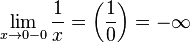_ или _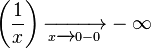

Если каждый элемент корабля был заменён хотя бы один раз, можно ли считать корабль прежним кораблём? В нашем организме каждый атом заменяется другим атомом того же элемента раз в 20-30 дней. Так можно ли считать, что человек остается тем же самым спустя 50 лет?

Этот парадокс возникает от того, что мы не дали определения ни кораблю, ни организму. Если корабль - множество именно этих деталей и никаких других, то при замене всех деталей мы несомненно имеем уже другой корабль. То же самое относится и к организму человека, если организм - то, что состоит именно из этих атомов.

· Но если корабль определить как систему, сущность которой определяется его свойствами как целого: весом, водоизмещением, скоростью, КПД и прочими характеристиками, то и при замене всех деталей аналогичными деталями корабль остается прежним. Свойства целого отличаются от свойств его частей и не сводятся к свойствам этих частей. Целое больше суммы его частей! Поэтому и в 50 лет человек остается самим собой, хотя 95% атомов его тела уже много раз за это время заменены другими, да и атомов в его теле становится больше, чем было в возрасте 10 лет.

· Так что не совсем прав был древний философ, заявив, что нельзя дважды войти в одну и ту же реку, так как вода в ней течет и все время молекулы ее в потоке заменяются. В этом случае неявно постулируется, что река - это сумма именно этих молекул воды и никаких других молекул воды. Но ведь это не так, ведь мы реку воспринимаем не как набор молекул воды, а как поток определенной глубины и ширины, с определенной скоростью течения, одним словом, река - это динамическая система, а не сумма своих частей.

· В арифметике при сложении, 1+1 = 2. Но ведь это может быть и не всегда так. Если к одному яблоку прибавить еще одно яблоко, то получится 2 яблока. Но если на это посмотреть по-другому и считать не яблоки, а абстрактные множества, то сложив 2 множества, мы получим еще третье, состоящее из двух множеств. То есть в этом случае 1 + 1 = 3, а может быть 1+1=1 (два множества слились в одно).

· А сколько будет 1+1+1? В обычной арифметике получается 3. А если учесть все комбинации из 3 элементов сначала по 2, а потом по 3? Правильно, в этом случае 1+1+1=6 (три сочетания по 1 элементу, два сочетания по 2 элемента и 1 сочетание по 3 элемента). Комбинаторная арифметика на первый взгляд кажется глупостью, но это так только с непривычки. В химии приходится считать сколько получится молекул воды, если взять 200 атомов водорода и 100 атомов кислорода. Получится 100 молекул воды. А если взять 300 атомов водорода и 100 атомов кислорода? Все равно получится 100 молекул воды и останется 100 атомов водорода. Итак, мы видим, что в химии находит себе применение иная арифметика. Подобные задачи имеют место и в экологии. Например, известно правило Либиха о том, что на растения оказывает влияние химический элемент в почве, который находится в минимуме. Даже если все другие элементы в большом количестве, растение сможет их усвоить столько, сколько позволяет элемент, находящийся в минимуме.