Парабола, каноническое уравнение. Эксцентриситет и директриса параболы

Параболой называется плоская кривая, в каждой точки которой выполняется следующее свойство: расстояние до заданной точки (фокуса параболы) равно расстоянию до заданной прямой (директрисы параболы). Расстояние от фокуса до директрисы называется параметром параболы и обозначается через p. Парабола имеет единственную ось симметрии, которая пересекает параболу в ее вершине. Каноническое уравнение параболы имеет вид: y = 2px.

Уравнение директрисы: x = −p/2,
где p − параметр параболы.

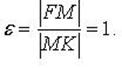
Эксцентриситет: Координаты фокуса: F(p/2, 0) Координаты вершины M(0, 0)

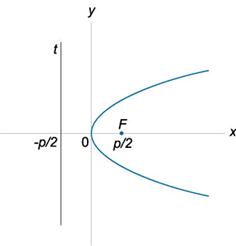
Общее уравнение параболы Ax² + Bxy + Cy² + Dx + Ey + F = 0, где B² − 4AC = 0.

Уравнение параболы, ось симметрии которой параллельна оси Oy: Ax² + Dx + Ey + F = 0 (A ≠ 0, E ≠ 0),
или в эквивалентной форме: y = ax² + bx + c, p = 1/(2a)

Уравнение директрисы: y = y₀ − p/2, где p − параметр параболы.

Координаты фокуса: F(x₀, y₀ + p/2)

Координаты вершины:

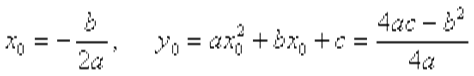
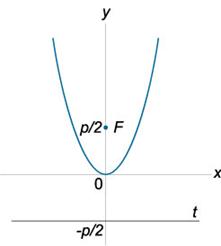Уравнение параболы с вершиной в начале координат и осью симметрии, параллельной оси Oy
y = ax², p = 1/(2a)

Уравнение директрисы y = −p/2, где p − параметр параболы.

Координаты фокуса: F(0, p/2) Координаты вершины: M(0, 0)