После того,как регрессионная модель специфицирована, производится ее параметризация. В случае парной линейной регрессионной модели 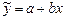 речь идет о количественной оценке коэффициентов a и b.
речь идет о количественной оценке коэффициентов a и b.
Наиболее распространенным методом оценки параметров регрессииявляется метод наименьших квадратов (МНК). Этот метод является наиболее простым с вычислительной точки зрения.
Суть МНК (отсюда и название метода) заключается в нахождении параметров модели, при которых минимизируется сумма квадратов отклонений эмпирических (реальных) значений 
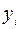 ,
, 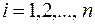 , зависимой переменной от теоретических значений
, зависимой переменной от теоретических значений 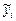
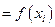 ,
, 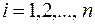 , полученных по уравнению регрессии:
, полученных по уравнению регрессии:
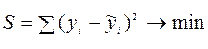 .
.
Функция 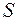 является функцией, аргументами которой являются неизвестные параметры уравнения регрессии. Исследование на экстремум данной функции проводится методами дифференциального исчисления. Для парного уравнения
является функцией, аргументами которой являются неизвестные параметры уравнения регрессии. Исследование на экстремум данной функции проводится методами дифференциального исчисления. Для парного уравнения 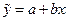 решается система двух уравнений, из которой находятся оценки неизвестных коэффициентов
решается система двух уравнений, из которой находятся оценки неизвестных коэффициентов 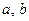 уравнения регрессии:
уравнения регрессии:
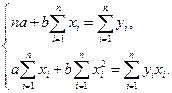 (1)
(1)
Решая систему, получим
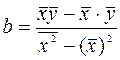 ,
, 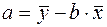 . (2)
. (2)
В уравнении 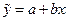 коэффициент b при переменной x указывает, на сколько изменится в среднем значение y при изменении фактора x на одну единицу измерения. Коэффициент a формально показывает прогнозируемый уровень y при x = 0. Правда, если x = 0 находится достаточно далеко от выборочных значений
коэффициент b при переменной x указывает, на сколько изменится в среднем значение y при изменении фактора x на одну единицу измерения. Коэффициент a формально показывает прогнозируемый уровень y при x = 0. Правда, если x = 0 находится достаточно далеко от выборочных значений 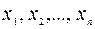 , то буквальная интерпретация может и не иметь ясного смысла.
, то буквальная интерпретация может и не иметь ясного смысла.
Свойства коэффициентов регрессии 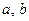 в модели
в модели 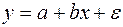 существенным образом зависят от свойств случайной составляющей
существенным образом зависят от свойств случайной составляющей 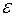 . Поэтому метод наименьших квадратов обеспечивает оптимальные свойства МНК-оценкам лишь при выполнении следующих классических модельных предположений:
. Поэтому метод наименьших квадратов обеспечивает оптимальные свойства МНК-оценкам лишь при выполнении следующих классических модельных предположений:
1. Математическое ожидание случайной переменной равно нулю.
2. Дисперсии случайных наблюдений одинаковы (это условие называется условием гомоскедастичности).
3. Случайные ошибки различных наблюдений являются независимыми между собой.
4. Объясняющая и случайная переменные независимы.
5. Случайная переменная имеет нормальный закон распределения вероятностей с нулевым математическим ожиданием и постоянной дисперсией.
Предположения 1–4 называются условиями Гаусса – Маркова, а предположение 5 – предположением о нормальности.
Линейная регрессионная модель, удовлетворяющая всем перечисленным выше условиям, называется классической нормальной линейной регрессионной моделью.
Теорема Гаусса–Маркова. Если условия 1 – 4 выполнены, то оценки коэффициентов парной линейной регрессии, полученные с помощью МНК, являются несмещенными, состоятельными и эффективными.
Теорема Гаусса–Маркова гарантирует, что:
а) в определении линии регрессии отсутствует систематическая ошибка;
б) при возрастании числа n наблюдений дисперсия оценок параметров регрессии стремится к нулю;
в) оценки имеют наименьшую дисперсию по сравнению с любыми другими оценками.
При определении оценок параметров нелинейных моделей парной регрессии применяют процедуру линеаризации. Она состоит в том, что с помощью преобразований переменных от каждого из уравнений переходят к рассмотрению соответствующего линейного уравнения относительно новых переменных, для которых справедливы формулы (2). В таблице 1 приведены виды регрессий и формулы оценок параметров.
Таблица 1
Оценки параметров нелинейных моделей регрессии
| Вид регрессии | Линеаризующее преобразование | Параметры уравнения регрессии |
Экспоненциальная регрессия 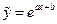 | 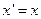 , , 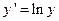 | 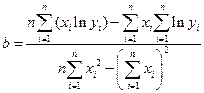 , , 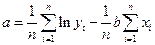 |
Логарифмическая регрессия 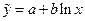 | 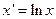 , , 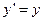 | 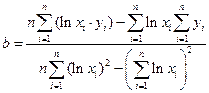 , , 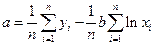 |
Степенная регрессия 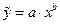 | 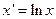 , , 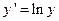 | 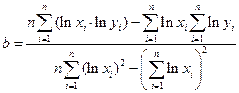 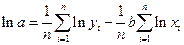 |
Показательная регрессия 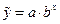 | 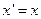 , , 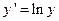 | 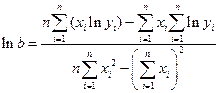 , , 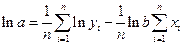 |
Гиперболическая регрессия 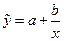 | 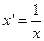 , , 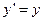 | 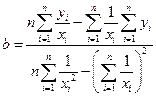 , , 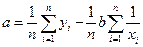 |
 2015-04-17
2015-04-17 1359
1359








