Линеаризация

При аналитическом получении моделей элементов в большинстве случаев приходится иметь дело с нелинейными дифференциальными уравнениями. Решать их можно численными методами с использованием вычислительных машин. Однако сами решения представляют собой лишь частные случаи, в то время как при решении линейных дифференциальных уравнений, пользуясь хорошо разработанной теорией, получаем аналитические решения, отражающие общность и обозримость для всех возможных случаев. С помощью аналитических решений возможны, как уже указывалось, не только количественные, но и качественные исследования моделей. Из сказанного следует, что продуктивность труда исследователя можно было бы существенно повысить, если бы удалось заменить с достаточной для практики точностью нелинейные уравнения соответствующими линейными уравнениями. Процесс такой замены носит название линеаризации.

Когда линеаризация возможна? Это далеко не праздный вопрос. Ведь если при замене нелинейного уравнения полученное линейное уравнение будет существенно отличаться от исходного нелинейного, ценность дальнейших исследований может быть сведена к нулю.

Рассмотрим в качестве примера маятник, показанный на рис.9.1. Уравнение момента для рассматриваемого маятника будет

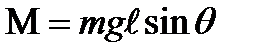, (9.1)

где m – масса; g – ускорение свободного падения; 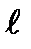- длина маятника, θ – угол отклонения от равновесного состояния, при котором θ = 0.

Нелинейная зависимость M = M(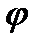) показана на рис.9.1,б.

Предположим, что рассматривается не абстрактный маятник, а маятник настенных часов. В этом случае можно говорить о том, что рабочий диапазон изменения угла θ приблизительно составляет [ 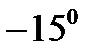, 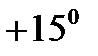]. Как следует из рис.9.1,б, на данном диапазоне нелинейная в целом зависимость M = M(θ) может быть рассмотрена как линейная в окрестности так называемой рабочей точки θ = 0, М = 0.

При этом уравнение (9.1) можно свести к виду

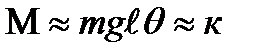
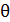, где к= mgl. (9.2)

а б

Рис.9.1. Маятник

Таким образом, учёт конкретных условий работы исследуемого объекта является основой для начала линеаризации.

Различают графическую и аналитическую линеаризацию. Первая используется чаще тогда, когда на основании проведённых экспериментов получены графические зависимости интересующих величин. Так, например, пусть имеется полученная таким образом графическая зависимость для клапана (рис.9.2).

Пусть известно, что в среднем в процессе работы клапана
y = 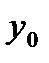= 60%, а диапазон изменения y равен [50 %,70 %], рабочая точка
А [60 %, 3 м³/ч]. Графическая линеаризация заключается в замене кривой касательной, проведённой к данной кривой в рабочей точке А (рис.9.2). Как видно из примера, наибольшая погрешность при такой замене возникает на границах рабочего интервала.

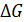
^G м³/ч

А

3 y

y (%)

0 b 50 60 70 100

Рис. 9.2. Характеристика клапана

Здесь G – расход жидкости, м³/ч, а y – степень открытия клапана, %

Математическое уравнение прямой, не проходящей через начало координат, будет иметь вид

G = ky + b, (9.3)

где k = tg 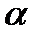, α и b указаны на рис.9.2.

Рассмотрим задачу несколько по-иному. Примем точку А за начало отсчёта, поскольку при работе клапана именно относительно неё происходит изменение y и G. При таком рассмотрении целесообразно ввести и новую систему координат с началом в точке А.

В новой система координат по оси абсцисс будет откладываться величина y = y - y₀, а по оси ординат - G = G - G₀,, т.е. отклонения величин y и G относительно их номинальных значений y₀ и G₀ соответственно.

В новой системе координат уравнение касательной в отклонениях запишется как

G = к y, (9.4)

Итак, имеем возможность получать уравнение касательной в двух видах:(9.3) и (9.4). Какой из них предпочесть с точки зрения удобства для исследования? Чтобы ответить на него решим насколько изменится расход, если степень открытия клапана изменится относительно y₀ на 5 %, на 10 % и т.п? Найти ответ проще во втором случае (9.4). Причем, определив ^G, например, при y = 5 %, величину ^G, при y = 10 % находим простым умножением предыдущего результата на 2. Это свойство линейных пропорциональных уравнений носит название гомогенности (однородности).0но позволяет инженеру быстро "прикинуть", к каким изменениям на выходе приведут те или иные изменения входного сигнала, что само по себе является одной из задач исследования.

Вместе с тем полезным оказывается еще одно свойство линейных пропорциональных уравнений – свойство суперпозиции или наложения.

Так, в случае сложного входного сигнала он может быть представлен суммой более простых в описании сигналов. Определив выходные сигналы на каждый из простых сигналов останется только просуммировать выходные сигналы и получить решение – выходной сигнал как реакцию на сложный входной сигнал.

C математической точки зрения это выглядит следующим образом

y=kx. (9.5)

Пусть x = x₁ + x₂ +…+ x_n, (9.6)

тогда y = k (x₁ + x₂ +…+ x_n) = k x₁+k x₂ +…+k x_n =
= y₁ + y₂ +…+y_n (9.7)

Учитывая сказанное, в дальнейшем уравнения звеньев будем получать в отклонениях сигналов от их номинальных значений и в форме не просто линейной, а именно линейной пропорциональной.

Отметим одно из важных обоснований возможности линеаризации моделей элементов АСР. Оно заключается в том, что в силу специфики работы АСР как регулируемая величина, так и другие величины, характеризующие состояние системы, меняются в силу специфики работы систем в достаточно малых пределах: колебания регулируемой величины не допускаются более заданной величины ошибки регулирования т.д. Наряду с графическим, существует аналитический метод линеаризации, основанный на использовании разложения функций в ряд Тейлора. Аналитическая линеаризация проводится в том случае, когда имеется математическая модель (нелинейная) исследуемого звена.

В качестве примера рассмотрим следующую модель звена: У= ах² Номинальные значения величин известны: У = У₀ и х = х₀.

Разложим исходную зависимость в окрестности рабочей точки в ряд Тейлора:

x0

x0

x0

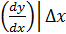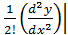
Y(x)= Y(x₀) + + х² + … (9.8)

При малых отклонениях Х пренебрегаем всеми членами разложения, начиная с третьего (при малом х, например, равном 0.1, х² будет равно 0,01, что с практической точки зрения существенно меньше). Тогда, переписывая уравнение (9.8), получим:

Y(x) 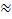Y(x₀) + 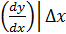. (9.9)

x0

Так как 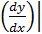= 2ах₀, можно записать

x0

Y = 2a х₀ x = k x. (9.10)

Полученное линейное пропорциональное уравнение в отклонениях представляет собой модель элемента при изменениях x и y вблизи рабочей точки с координатами (x₀ ,y ₀ ). Как следует из уравнения (9.9), от выбора значения x₀ зависит величина коэффициента пропорциональности k и, следовательно, близость линейной модели к исходной нелинейной.

Пользуясь полученными моделями при расчетах систем, следует понимать, что результаты расчетов будут отличаться от реальности. Для этого необходимо сравнить расчетные данные с полученными данными работающей системы.

Если расхождения будут велики, следует вернуться к оценке правильности проведенной линеаризации.

Внимание. Поскольку процесс линеаризации зависимостей обязателен и его результат получается всегда в отклонениях величин от их номинальных значений, в дальнейшем для экономии чернил и времени знак в уравнениях опускается.

Помнить о том, что дело приходится иметь с отклонениями от рабочих значений, а не с самими величинами - нужно постоянно.