Модели сигналов

Модели элементов и систем - это математическое описание связи входных и выходных сигналов. Процесс исследования работы элементов и систем с использованием их математических моделей носит название моделирования. Моделирование можно проводить, пользуясь ручкой или компьютером. С компьютером, имея специализированные пакеты прикладных программ для расчета систем, проводить расчеты целесообразнее: выше производительность труда проектировщика, возможность быстрого перебора многих вариантов решения задачи проектирования систем, нулевая вероятность ошибок в расчетах и т.п.

Однако в любом случае следует понимать основные вещи. Расчет систем сводится к выбору элементов систем, их параметров, при которых системы будут справляться со стоящими перед ними задачами.

Подбирая параметры (коэффициенты уравнений) о результатах выбора можно делать выводы, имея картину изменения регулируемой величины во времени.

Обычно это графики изменения регулируемой величины во времени.

Для того, чтобы получить подобные результаты, необходимо определиться с входными сигналами. Так, для систем, различных по назначению, требуется рассматривать различные виды задающего воздействия. А моделируя работу систем при возмущениях, необходимо иметь представление о реальных возмущающих воздействиях, их характере и величинах.

Рассмотрим:

Во-первых, поведение любого объекта во времени зависит от действующего на него воздействия, от состояния самого объекта в момент начала действия воздействия и от собственных свойств.

Так, например, полет мяча будет зависеть от характера и силы удара по нему, от того, стоял или подлетал мяч к моменту удара (это, так называемые, начальные условия) и от его параметров (размера, веса).

Вычленить в последующем после удара полете мяча, что в этом полете обусловлено воздействием, что зависит от начальных условий, а что от собственных свойств не представляется возможным.

Однако узнать для одинаковых по форме, но разных по массе мячей о данной разнице можно по их полету. Начать нужно с того, чтобы оба находились в покое и ударить с одинаковой силой. Разница траекторий скажет о разнице свойств мячей, кто тяжелее.

То же касается и исследований свойств элементов и систем.

Так как основной целью расчетов является выбор параметров элементов, это вынуждает ограничить причины различного поведения объектов.

Первое из ограничений – это принятие начальных условий нулевыми.

Второе – один и тот же вид сигнала при исследовании элементов и систем.

Такие ограничения приводят к тому, что, сравнивая элементы систем, появляется возможность оценить разницу их свойств по реакциям на один и тот же входной сигнал при одних и тех же начальных условиях. Вместе с тем, подбирая элементы систем и их параметры, по полученным в результате моделирования картинам изменения регулируемой величины, можно делать вывод о пользе или нежелательности сделанных изменений.

Вторая проблема связана с необходимостью проводить расчеты с данными, соответствующими реальным условиям работы систем. Это значит, что на определенном этапе расчетов необходимо исследовать работу системы при реальных входных сигналах. Для этого нужно или иметь сведения о таких сигналах, либо, если это невозможно, приблизительно «прикинуть» какими они могут быть.

Последнее, что следует заметить, сигналы должны быть достаточно просты в математическом описании, чтобы не усложнять неоправданно расчеты.

Выигрыш от введения стандартных сигналов, называемых в дальнейшем «типовыми», несомненен.

Он позволяет

· Классифицировать элементы систем по их динамическим свойствам

· Связать эти свойства с свойствами систем

· Провести стандартизацию характеристик звеньев

· Стандартизировать оценку качества работы систем и т. п.

К таким так называемым типовым воздействиям относятся (рис. 10.1)

· Единичное ступенчатое воздействие

· Дельта - функция

· Линейно меняющийся во времени сигнал

· Сигнал, меняющийся по параболическому закону.

1(t) 1(t- τ) 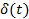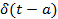x_вх= vt x_вх=at²

1 1

t t t t t

τ a

Рис.10.1. Типовые воздействия

Единичное ступенчатая функция (единичное ступенчатое воздействие) обладает следующими свойствами: ее вид – ступенька, а величина ступеньки равна единице (рис. 10.1):

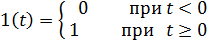
Дельта- функция Дирака

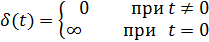
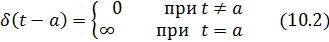
Реализовать на практике сигнал равный бесконечности невозможно (как и многое в математике). Стоит отметить, что сам Дирак не вполне понимал суть придуманной им функции. Но дальнейшее ее использование в расчетах, в написании формул показало, что польза от ее применения реальна. Одно из ее свойств можно трактовать как реальное: площадь под данной функцией равна 1. Так как площадь ассоциируется с понятием энергии можно сказать, что «энергия», заключенная в этой функции конечна.

Вместе с тем данная функция позволяет выделять в любой другой функции ее значение в конкретный момент времени

что позволяет корректно записывать некоторые математические выражения.

Например, x(t)= .

Для нее

налицо и сама функция и ее значение в конкретный момент времени.

К другим типовым сигналам относят

линейную функцию

x_вх= vt (10.6)

и параболическую функцию

x_вх= at² (10.7)

Несмотря на простоту рассмотренных функций, их можно использовать для решения сложных задач, рассматривая сложные по характеру сигналы как сумму типовых сигналов.

Рассмотрим пример. Бак, из которого снабжается водой поселок. Для обеспечения постоянного напора воды потребителю необходимо поддерживать постоянное значение уровня воды в баке.

Решая задачу проектирования системы регулирования уровня воды в баке, необходимо оценить, будет ли система должным образом поддерживать уровень воды при действии возмущений.

В качестве одного из возмущающих воздействий рассмотрим изменение расхода воды потребителем, которое влияет на уровень воды в баке. Информацию о расходе можно получить, используя расходомер.

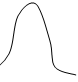
Пусть, фиксируя данный расход за сутки, получили его график рис.10.2.

G^,м3/ч

G,м³/ч

G1

t,ч

G2

G₀ 0

t,ч

0 1 6 8

0 t,ч

8 16 24

Рис.10.2. График изменения расхода воды из бака

График по одному дню вряд ли показателен. В будни будет фиксироваться одно, в выходные – другое изменение расхода. Весной и летом также будут отличия.

Из математики известно, что любая кривая может быть описана с различной степенью точности полиномом n-го порядка. Так полином 10-го порядка даст совпадение описания кривой в 10-ти точках. В промежутках совпадения не будет. Но, если оставить вопросы точности описания в стороне, сложность выражения повлечет и сложность расчетов.

Так ли потребно описывать весь график? Из приведенного графика можно сделать важный вывод о том, когда системе сложнее решить задачу поддержания требуемого значения уровня воды. Это временной интервал от 16 до 24 часов, поскольку на данном участке большие изменения в расходе воды будут приводить к необходимости приложения больших усилий и большей оперативности системы по удержанию требуемого значения уровня воды. Далее можно сделать вывод о том, что если проектируемая система на этом интервале справится с задачами, то на менее сложных участках она тем более справится. Данные рассуждения позволяют упростить задачу получения математической модели, математического описания изменения расхода воды.

Следующий шаг – описать сложный сигнал через типовые сигналы, т.е. представить сложный сигнал в виде суммы простейших типовых сигналов, например, в виде ступенчатых функций

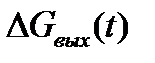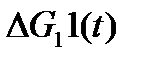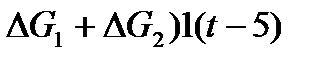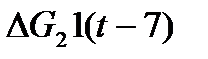= -( + (10.8)

В этом случае нахождение выходного сигнала (уровня воды) осущест-вляется с использованием принципов суперпозиции и гомогенности:
вычислив h(t) при 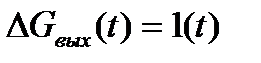, находятся
h₁(t) = ,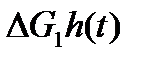
h₂(t-5) = -(,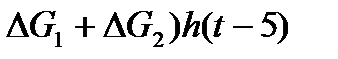
h₃(t-7) =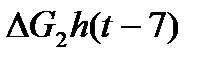
и затем, суммируя, находится изменение уровня
h_сумма(t)= h₁(t) + h₂(t-5)+ h₃(t-7).

Достоинством ступенчатой функции является не только простота проводимых с ее помощью расчетов и их малая трудоемкость, но и простота ее реализации на действующих объектах. Так расход 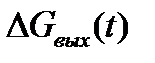можно изменить скачком, приоткрыв заслонку на выходе из бака. Полученное изменение уровня можно сравнить с изменением уровня, рассчитанное на основании математической модели и сделать выводы о точности математического описания.

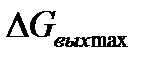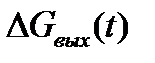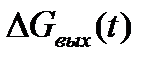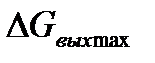
Остановимся далее на случае, когда реально выполненного элемента не существует, а даны лишь основные характеристики. Так, для бака можно представить, например, лишь максимально возможное значение . Какую модель входного сигнала взять в этом случае? Одним из возможных ответов будет следующий: = 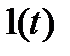. Такое изменение расхода воды в действительности маловероятно и соответствовало бы для АСР одному из наиболее тяжёлых режимов её работы: удержанию уровня воды при резком изменении расхода. Тем не менее, если при проектировании системы удаётся обеспечить требуемое качество её функционирования, это гарантирует удовлетворительную работу системы при менее тяжёлых воздействиях.

Наряду с рассмотренными типовыми сигналами для расчёта систем используют также гармонический сигнал X(t) = A sin 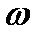t. Его применение связано с методом Фурье, согласно которому любая функция f(t) может быть представлена как совокупность простейших гармонических составляющих:

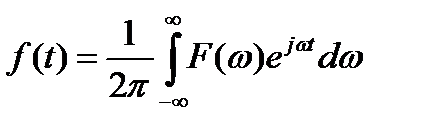, (10.9)

где 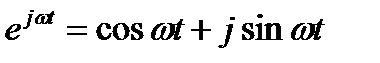, (10.10)

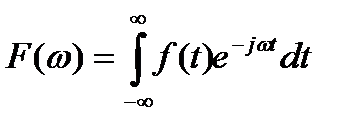. (10.11)

Для линейных АСР задача определения их реакции на f(t) сводится, по сути, к суммированию реакций на простейшие гармонические составляющие f(t). Методы анализа систем, основанные на таком представлении сигналов, носят название частотных методов. Несколько иной подход заключается в исследовании АСР на так называемое синусоидальное воздействие. Смысл его состоит в следующем.

Пусть известны максимально возможная скорость 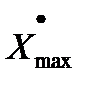и ускорение 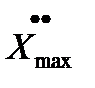входного сигнала X(t).

Сформируем такой гармонический сигнал 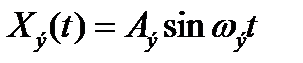, который имел бы 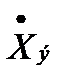= 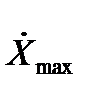и = .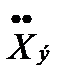

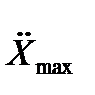Итак, пусть

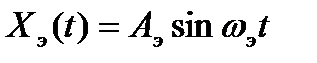(10.12)

Продифференцируем 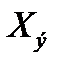(t) дважды:

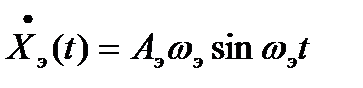, (10.13)

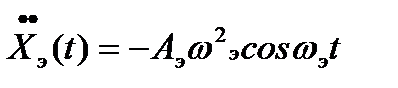. (10.14)

Приравняем

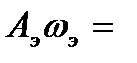
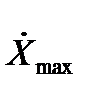, (1 0. 15)

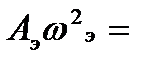
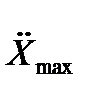; (10.16)

из уравнений (1 0. 15) и (10.16) получим

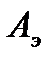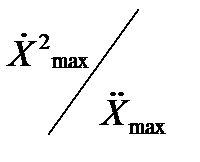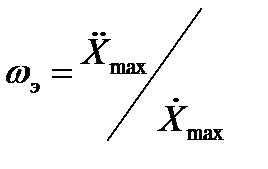
= и . (10.17)

Как следует из метода получения эквивалентного гармонического сигнала 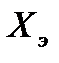(t), он представляет собой наиболее сложное воздействие. Если удаётся рассчитать систему, удовлетворяющую требованиям к качеству её работы при 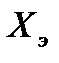(t), то, очевидно, что при воздействиях менее сложных её функционирование будет удовлетворительным.