Раскрытие неопределенностей вида 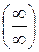 и
и 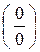 .
.
Рассмотрим предел частного двух функций 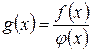 при
при 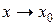 , имеющих предел в точке x 0. При этом возможны следующие случаи:
, имеющих предел в точке x 0. При этом возможны следующие случаи:
1. 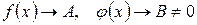 , тогда по теореме 4.7
, тогда по теореме 4.7 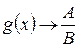 .
.
2. 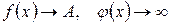 , тогда
, тогда 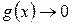 .
.
3. 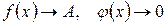 , тогда
, тогда 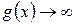 .
.
4. 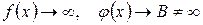 , тогда
, тогда 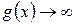 .
.
5. 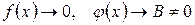 , тогда
, тогда 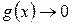 .
.
6. 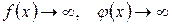 .
.
7. 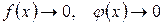 .
.
В последних двух случаях частное двух функций может стремиться к любому пределу – к константе, нулю или бесконечности. В таких случаях говорят, что мы имеем дело с неопределенностью. Случай 6 называется неопределенностью вида 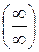 , а случай 7 – неопределенностью вида
, а случай 7 – неопределенностью вида 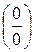 . Нахождение предела числовой последовательности или функции в случае наличия неопределенности называется раскрытием неопределенности. Познакомимся с основными методами раскрытия неопределенностей на примерах.
. Нахождение предела числовой последовательности или функции в случае наличия неопределенности называется раскрытием неопределенности. Познакомимся с основными методами раскрытия неопределенностей на примерах.
1. Раскрытие неопределенности вида 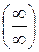 .
.
Пример 4.1. Найти предел 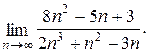
Очевидно, что при 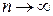 числитель и знаменатель дроби стремятся к бесконечности. Действительно, с ростом n слагаемые многочленов, содержащие старшие степени n будут намного больше остальных слагаемых. Для раскрытия неопределенности вида
числитель и знаменатель дроби стремятся к бесконечности. Действительно, с ростом n слагаемые многочленов, содержащие старшие степени n будут намного больше остальных слагаемых. Для раскрытия неопределенности вида 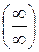 разделим числитель и знаменатель дроби на n в самой высокой (старшей) степени для обоих многочленов (т.е. на n 2). Получим:
разделим числитель и знаменатель дроби на n в самой высокой (старшей) степени для обоих многочленов (т.е. на n 2). Получим:
|
|
|
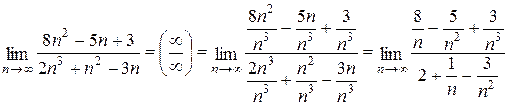 .
.
С ростом n выражения 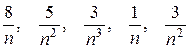 стремятся к нулю. Последовательно применяя теоремы 4.3 и 4.1, получим:
стремятся к нулю. Последовательно применяя теоремы 4.3 и 4.1, получим:
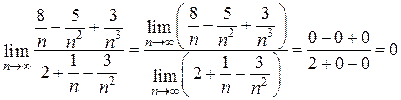 .
.
Задача 4.2. Найти предел 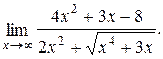
Решение. Для раскрытия неопределенности вида  разделим числитель и знаменатель дроби на x 2. Получим:
разделим числитель и знаменатель дроби на x 2. Получим:
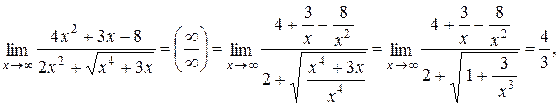
так как при 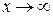 выражения
выражения 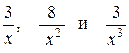 стремятся к нулю.
стремятся к нулю.
2. Раскрытие неопределенности вида 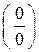 .
.
Пример 4.3. Найти предел 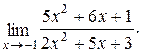
При подстановке вместо x числа –1 мы получаем неопределенность вида 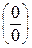 . Для раскрытия этой неопределенности разложим многочлены, стоящие в числителе и знаменателе дроби, на множители. При этом один из корней, как числителя, так и знаменателя равен –1. Второй корень найдем по теореме Виета. Для числителя
. Для раскрытия этой неопределенности разложим многочлены, стоящие в числителе и знаменателе дроби, на множители. При этом один из корней, как числителя, так и знаменателя равен –1. Второй корень найдем по теореме Виета. Для числителя 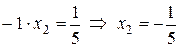 . Для знаменателя
. Для знаменателя 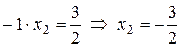 . Итак,
. Итак,
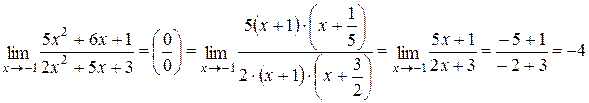 .
.
После сокращения числителя и знаменателя на (x + 1) ¹ 0 неопределенность пропадает и предел легко вычисляется с помощью подстановки x = –1.
Задача 4.4. Найти предел 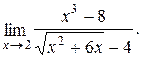
Решение. При подстановке вместо x числа 2 мы получаем неопределенность вида 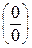 . Для раскрытия этой неопределенности сначала избавимся от иррациональности в знаменателе дроби, а затем разложим выражения, стремящиеся к нулю, на множители:
. Для раскрытия этой неопределенности сначала избавимся от иррациональности в знаменателе дроби, а затем разложим выражения, стремящиеся к нулю, на множители:
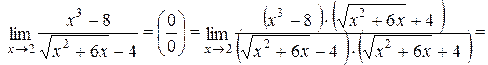
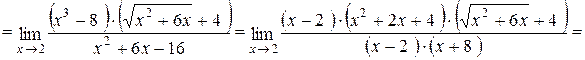
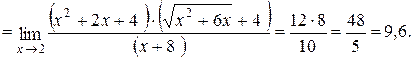
3. Раскрытие неопределенностей вида 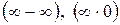 .
.
Пределы, содержащие неопределенности вида 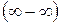 или
или 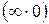 обычно с помощью алгебраических преобразований сводят к пределам, содержащим неопределенности вида
обычно с помощью алгебраических преобразований сводят к пределам, содержащим неопределенности вида 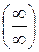 или
или 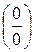 .
.
Пример 4.5. Найти предел 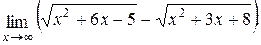 .
.
Очевидно, что при  уменьшаемое и вычитаемое стремятся к бесконечности. Для раскрытия неопределенности
уменьшаемое и вычитаемое стремятся к бесконечности. Для раскрытия неопределенности 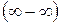 сначала превратим разность в частное двух функций, умножив и разделив ее на сопряженное выражение. Получив неопределенность вида
сначала превратим разность в частное двух функций, умножив и разделив ее на сопряженное выражение. Получив неопределенность вида 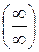 , раскроем ее с помощь деления числителя и знаменателя полученной дроби на старшую степень x:
, раскроем ее с помощь деления числителя и знаменателя полученной дроби на старшую степень x:
|
|
|
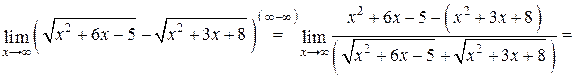
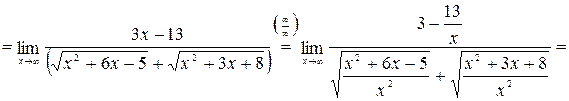
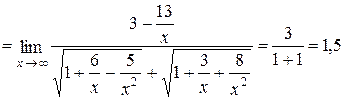 .
.
Задача 4.6. Найти предел 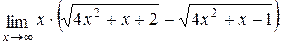 .
.
Решение. Нетрудно установить, что предел второго сомножителя равен нулю (проверьте самостоятельно). Следовательно, в данном примере мы имеем дело с неопределенностью вида 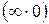 . Для раскрытия этой неопределенности умножим и разделим исходную функцию на сумму
. Для раскрытия этой неопределенности умножим и разделим исходную функцию на сумму 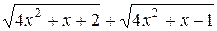 . Получив неопределенность вида
. Получив неопределенность вида 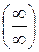 , раскроем ее с помощью деления числителя и знаменателя полученной дроби на x:
, раскроем ее с помощью деления числителя и знаменателя полученной дроби на x:
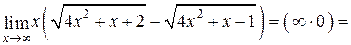
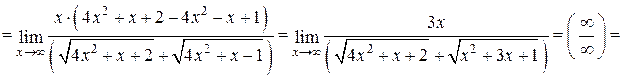
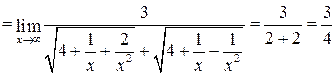 .
.
 2015-04-01
2015-04-01 1120
1120








