1. Полная энергия 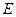 классического гармонического осциллятора может принимать любые положительные значения, начиная с
классического гармонического осциллятора может принимать любые положительные значения, начиная с 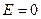 . При
. При 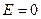 частица покоится в начале координат. В квантовом случае результат принципиально иной. Полная энергия может принимать только дискретные значения
частица покоится в начале координат. В квантовом случае результат принципиально иной. Полная энергия может принимать только дискретные значения 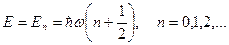 Спектр энергий эквидистантный
Спектр энергий эквидистантный 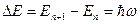 - независит от
- независит от 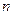 . Наименьшее значение[l5] энергии
. Наименьшее значение[l5] энергии 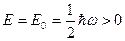 называется энергией нулевых колебаний.
называется энергией нулевых колебаний.
2. Средние значения координаты и импульса классического осциллятора равны нулю: 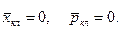 Для квантового осциллятора среднее значение координаты и импульса соответственно равны:
Для квантового осциллятора среднее значение координаты и импульса соответственно равны:
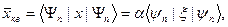
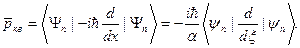
Учитывая выражения (s.25), (s.26) находим
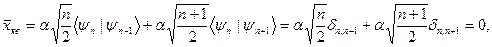
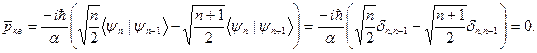
Здесь учтено, что функции 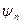 образуют полный ортонормированный набор, так, что
образуют полный ортонормированный набор, так, что
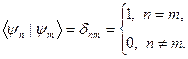
Таким образом, и для классического и квантового осциллятора средние значения координат и импульса равны нулю.
3. Для модели классического гармонического осциллятора его энергия связана со среднеквадратичным отклонением от положения равновесия выражением
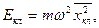
где черта сверху означает среднее по периоду колебаний 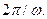 Проверим выполняется ли подобное соотношение в квантовом случае. Для этого вычислим, используя формулы (s.25), (s.26), среднеквадратичные флуктуации координаты в произвольном состоянии
Проверим выполняется ли подобное соотношение в квантовом случае. Для этого вычислим, используя формулы (s.25), (s.26), среднеквадратичные флуктуации координаты в произвольном состоянии 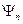 . Имеем
. Имеем
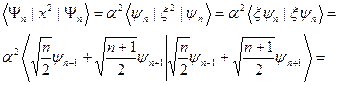
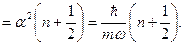
С учетом выражения для спектра энергии 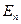 в (s.24), получаем
в (s.24), получаем
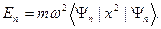
Таким образом, и в классическом и квантовом случаях, связь между энергией и среднеквадратичными отклонениями от положения равновесия одинакова.
4. Для классического осциллятора имеет место теорема вириала: 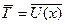 , где
, где 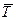 - средняя по периоду колебаний кинетическая энергия частицы. Какова связь между средней кинетической и потенциальной энергиями осциллятора в произвольном квантовом состоянии
- средняя по периоду колебаний кинетическая энергия частицы. Какова связь между средней кинетической и потенциальной энергиями осциллятора в произвольном квантовом состоянии 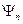 ? Рассмотрим среднее
? Рассмотрим среднее
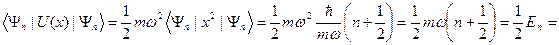
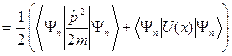 .
.
Отсюда, непосредственно, следует
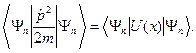
Таким образом, и в квантовом случае средняя кинетическая энергия равна средней потенциальной энергии, т.е. теорема вириала выполняется.
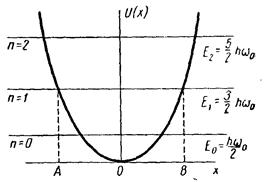
5.1. Обсудим некоторые особенности квантовых состояний гармонического осциллятора. На рис. представлена диаграмма квантовых уровней 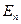 и потенциальной энергии
и потенциальной энергии 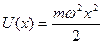 . Для примера рассмотрим квантовый уровень с энергией
. Для примера рассмотрим квантовый уровень с энергией 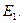 В классическом случае частица с такой энергией может совершать колебательные движения между точками
В классическом случае частица с такой энергией может совершать колебательные движения между точками 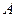 и
и 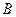 (точками поворота, где кинетическая энергия обращается в ноль). Обозначим амплитуду колебаний через
(точками поворота, где кинетическая энергия обращается в ноль). Обозначим амплитуду колебаний через 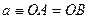 и определим вероятность
и определим вероятность 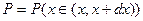 нахождения частицы в области
нахождения частицы в области 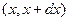 , лежащей внутри отрезка
, лежащей внутри отрезка 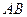 .
.
Эта вероятность равна

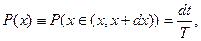
где 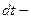 время, за которое частица проходит расстояние
время, за которое частица проходит расстояние 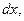 а
а 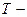 период колебаний. Пусть период
период колебаний. Пусть период 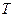 колебаний равен
колебаний равен 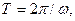 тогда
тогда
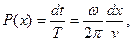
где 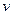 - скорость частицы. Выразим скорость частицы через переменную
- скорость частицы. Выразим скорость частицы через переменную 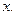 Для простоты положим, что решение уравнения движения для классического осциллятора имеет вид
Для простоты положим, что решение уравнения движения для классического осциллятора имеет вид 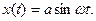 Отсюда
Отсюда
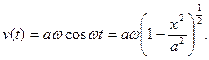
Таким образом, искомая вероятность равна
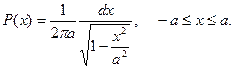 (s.27)
(s.27)
Выражение, стоящее перед 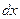 представляет собой, очевидно, плотность вероятности. Обозначим ее как
представляет собой, очевидно, плотность вероятности. Обозначим ее как 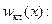

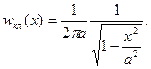 (s.28)
(s.28)
Заметим, что для распределения (s.28) условие нормировки 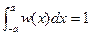 выполняется. Из вида распределения (s.28) видно, что функция имеет минимум в точке
выполняется. Из вида распределения (s.28) видно, что функция имеет минимум в точке 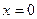 , в точках поворота
, в точках поворота 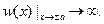 Таким образом, вероятность встретить частицу в центральной области мала из-за того, что здесь скорость частицы максимальна, в окрестности точек поворота скорость мала и вероятность встретить частицу больше.
Таким образом, вероятность встретить частицу в центральной области мала из-за того, что здесь скорость частицы максимальна, в окрестности точек поворота скорость мала и вероятность встретить частицу больше.
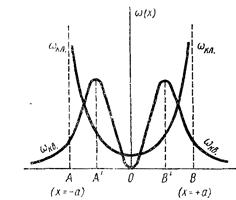
Рассмотрим квантовый гармонический осциллятор. Вероятность найти частицу в области 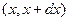 в произвольном квантовом состоянии
в произвольном квантовом состоянии 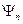 равна
равна
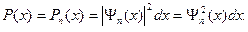 (s.29)
(s.29)
В состоянии 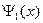 с энергией
с энергией 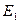
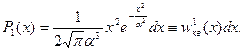 (s.30)
(s.30)
Распределение 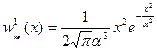 имеет три точки экстремума - точка минимума
имеет три точки экстремума - точка минимума 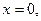 и две точки максимума
и две точки максимума 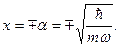 (точки
(точки 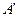 и
и 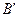 соответственно). Для уровня
соответственно). Для уровня 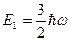 точки поворота
точки поворота 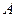 и
и 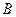 имеют координаты
имеют координаты 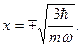 Важно, что распределение
Важно, что распределение 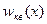 определено и за пределами точек поворота, т.е. имеется отличная от нуля вероятность найти частицу вне области
определено и за пределами точек поворота, т.е. имеется отличная от нуля вероятность найти частицу вне области 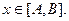
5.2. Вычислим дисперсии координаты и импульса в произвольном квантовом состоянии. Так как средняя координата и средний импульс для квантового осциллятора равны нулю, имеем
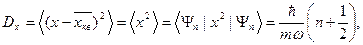
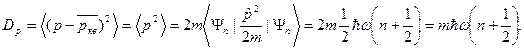
Определим произведение 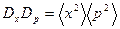 . Имеем
. Имеем
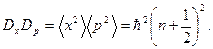
Таким образом,
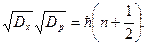 (s.31)
(s.31)
В основном состоянии 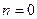 в соотношении неопределенности реализуется равенство
в соотношении неопределенности реализуется равенство
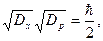 (s.32)
(s.32)
т.е. нулевая энергия есть наименьшая энергия, совместимая с соотношением неопределенностей.
Для произвольных 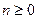 [l6]
[l6]
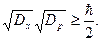 (s.33)
(s.33)
Таким образом, соотношение неопределенностей выполняется для состояний квантового гармонического осциилятора
При низких температурах атомы в молекуле или твердом теле совершают малые колебания вблизи положения равновесия. Экспериментальные исследования рассеяния света кристаллами показали, что при понижении температуры интенсивность рассеянного света стремиться не к нулю (как это следует из классической теории), а стремиться к некоторому предельному значению, даже в области абсолютного нуля температуры. Потенциальную энергию при низких температурах вблизи положения равновесия можно аппроксимировать квадратичным потенциалом и поэтому модель квантового гармонического осциллятора является здесь хорошим приближением. Рассмотрение в рамках этой модели действительно указывает на существование нулевых колебаний, отвечающих основному состоянию с энергией 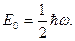
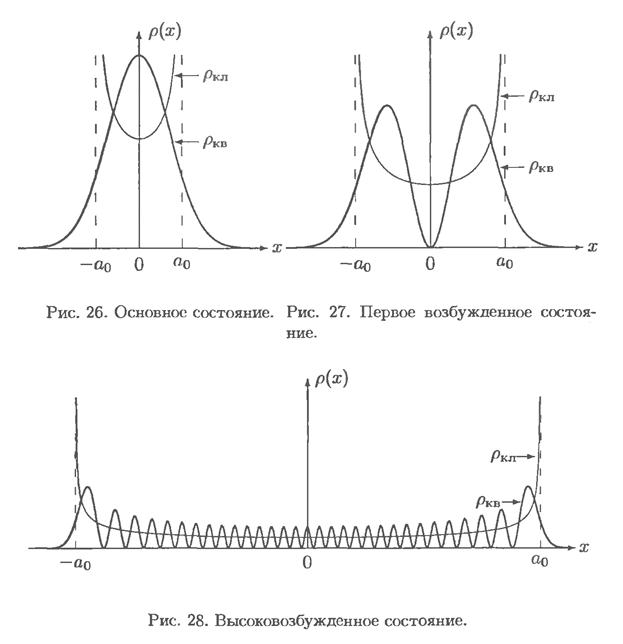
В заключение пункта 5 отметим, что как это следует из обсуждения, основное состояние с 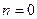 и ближайшие к нему возбужденные состояния сильно отличаются от классических. Сильно возбужденные состояния с
и ближайшие к нему возбужденные состояния сильно отличаются от классических. Сильно возбужденные состояния с 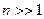 , напротив, мало отличаются от классических.
, напротив, мало отличаются от классических.
В общем случае, распределение координат частицы в произвольном квантовом состоянии с волновой функцией 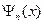 , описывается зависимостью (s.29). В основном состоянии распределение координат частицы представляет собой хорошо известное в теории вероятностей гауссово распределение:
, описывается зависимостью (s.29). В основном состоянии распределение координат частицы представляет собой хорошо известное в теории вероятностей гауссово распределение:
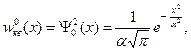 (s.33)
(s.33)
показывающее, что частица в этом состоянии локализована в центральной области (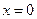 - точка максимума). Для классического осциллятора распределение
- точка максимума). Для классического осциллятора распределение 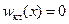 при
при 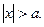 В квантовом же случае
В квантовом же случае 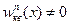 при
при 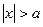 и существует отличная от нуля вероятность обнаружить частицу за пределами потенциальной ямы. При этом вероятность убывает экспоненциально за пределами области
и существует отличная от нуля вероятность обнаружить частицу за пределами потенциальной ямы. При этом вероятность убывает экспоненциально за пределами области 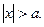 При
При 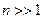 распределение
распределение 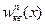 квантовой частицы сильно осциллирует в области
квантовой частицы сильно осциллирует в области 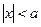 , амплитуда осцилляций уменьшается и в среднем
, амплитуда осцилляций уменьшается и в среднем 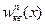 приближается к
приближается к 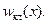
Правила отбора. Интенсивность дипольного и квадрупольного излучения
Обсудим, не вдаваясь в подробности, задачу об излучении квантового гармонического осциллятора. На этой задаче будет проиллюстрирована еще одна особенность квантовых систем, связанная с так называемыми правилами отбора.
Дипольные переходы. Интенсивность спонтанного излучения (т.е. энергия излучения в единицу времени) с вышележащего уровня 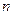 , с энергией
, с энергией 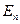 на низколежащий уровень
на низколежащий уровень 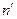 с энергией
с энергией 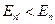 равна
равна
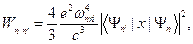 (s.34)
(s.34)
где 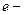 заряд,
заряд, 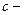 скорость света,
скорость света, 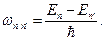 Совокупность
Совокупность 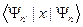 образуют матрицу. Для вычисления матричного элемента
образуют матрицу. Для вычисления матричного элемента 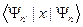 воспользуемся рекуррентными соотношениями для собственных функций
воспользуемся рекуррентными соотношениями для собственных функций
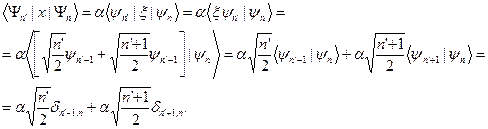
(s.35)
Из выражения (s.35) следует, что отличными от нуля будут только те матричные элементы 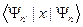 (разрешенные переходы), для которых
(разрешенные переходы), для которых 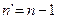 или
или 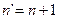 , т.е. правила отбора для квантового состояния
, т.е. правила отбора для квантового состояния 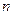 будут определяться формулой:
будут определяться формулой:
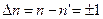 . (s.35)
. (s.35)
Из правил отбора вытекает, что переходы возможны только между соседними уровнями.
В соответствие с правилами отбора имеем следующие отличные от нуля матричные элементы, связанные с дипольными переходами:
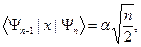
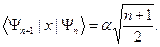 (s.36)
(s.36)
Напомним, что 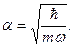
Для частоты излучения 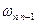 , получаем
, получаем
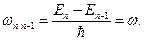
Поскольку спонтанные переходы возможны сверху вниз (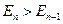 ), в соответствие с (s.34) для интенсивности излучения гармонического осциллятора
), в соответствие с (s.34) для интенсивности излучения гармонического осциллятора 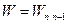 находим
находим
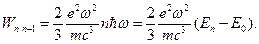 (s.37)
(s.37)
В области больших квантовых чисел 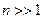 , когда
, когда 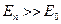 и в (s.37)
и в (s.37)
можно пренебречь энергией нулевых колебаний, полученное при этом выражение совпадает по форме результатом классического рассмотрения излучения гармонического осциллятора 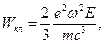 где под
где под 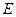 понимается энергия гармонического осциллятора
понимается энергия гармонического осциллятора 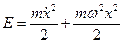 усредненная по периоду колебаний
усредненная по периоду колебаний 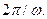
Квадрупольные переходы.
[l1]Обозначения на графике
[l2]Отметить важность этого
[l3]Нормировочны коэффициент7
[l4]Полнота?
[l5]Подчекнуть
[l6]Не хватает фразы
 2015-04-17
2015-04-17 3866
3866






