Условия задачи. Электромагнитная волна частотой 20 МГц под углом 45˚ падает из вакуума на границу с морской водой, имеющей следующие характеристики: ε2 = 80, μ2 = 1, σ2 = 4 См/м. Определить коэффициенты отражения и прохождения при параллельной поляризации падающей волны, а также коэффициент затухания.
Решение. Вначале определим, к какому классу относится отражающая среда - к диэлектрикам, проводникам или полупроводникам. Для этого по формуле (3.1) рассчитаем тангенс угла диэлектрических потерь:
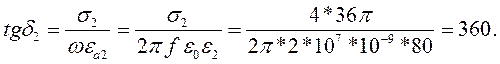
|
Таким образом, морская вода на частоте 20 МГц является проводником. Поэтому определять угол прохождения не надо: для проводников он равен нулю. То есть прошедшая электромагнитная волна распространяется в проводнике по нормали к поверхности.
Для расчета коэффициентов отражения и прохождения осталось определить волновые сопротивления сред. При этом волновое сопротивление среды 1, из которой падает волна, определено: Z1 = Z0 = 120π. Для определения волнового сопротивления среды 2 необходимо воспользоваться формулой (3.19):
|
|
|
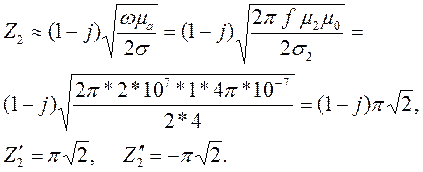
|
Для упрощения расчетов целесообразно предварительно вычислить косинус угла падения: cos φ = cos 45˚ = 0.707.
Таким образом, имеющихся данных достаточно для того, чтобы по формулам (2.11) - (2.14) определить модули и аргументы коэффициентов отражения и преломления:
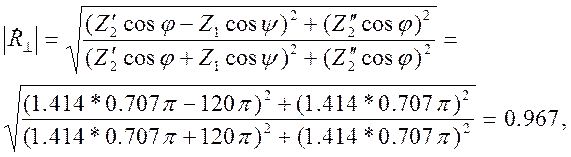
|
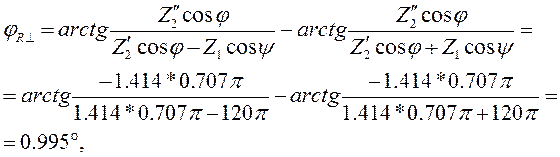
|
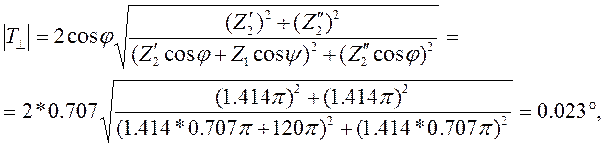
|
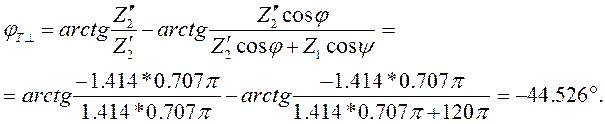
|
Осталось определить коэффициент затухания. Для этого есть формула (3.20). Из нее следует формула для расчета коэффициента затухания:
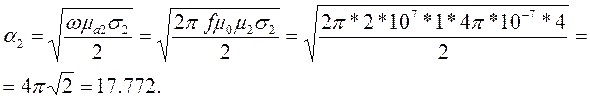
|
Задача решена.
ЛИТЕРАТУРА
1. Никольский, В.В. Электродинамика и распространение радиоволн / В.В. Никольский, Т.И. Никольская. М: Наука, 1989. – 544 с. – ISBN 5-02-014033-3.
2. Петров, Б.М. Электродинамика и распространение радиоволн / Б.М. Петров. М.: Горячая линия – Телеком, 2007. – 558 с.
 2015-04-01
2015-04-01 431
431







