Свойства несовместных событий
Пусть дана система несовместных событий А 1, А 2, …, Аn (т.е. любые два события несовместны). Справедливы следующие утверждения:
Теорема 1. Если система событий А 1, А 2, …, Аn является несовместной, то вероятность суммы этих событий равна сумме их вероятностей:
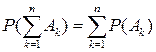 (5)
(5)
Теорема 2. Если система событий А 1, А 2, …, Аn является полной (т.е. сумма всех этих событий есть событие достоверное) и несовместной, то сумма вероятностей этих событий равна 1:
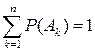 (6)
(6)
Противоположные события
Два события называются противоположными по отношению к данному испытанию, если они образуют полную и несовместную систему. Обозначение: А и 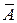 - противоположные события.
- противоположные события.
Согласно определению: 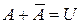 и
и 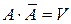 . Тогда из теоремы 2 следует, что
. Тогда из теоремы 2 следует, что
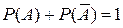 . (7)
. (7)
Вероятность суммы событий
Если события несовместны по отношению к данному испытанию, то вероятность их суммы вычисляется по формуле (5): P (A + B)= P (A)+ P (B).
В общем случае, для любых двух событий А и В справедливо равенство:
P (A + B)= P (A)+ P (B) - P (AB) (8)
Условная вероятность
|
|
|
Условной вероятностью события А при гипотезе В называется вероятность события А при таком условном испытании, по отношению к которому событие В является достоверным. Обозначение: P(A/B).
По отношению к классическому определению вероятности для любых событий А и В справедлива формула:
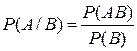 (9)
(9)
Вероятность произведения событий
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при гипотезе первого:
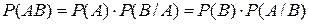 (10)
(10)
Событие А называется независимым от события В, если 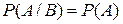 . В противном случае событие А называется зависимым от события В. Нетрудно показать, что если событие А не зависитот события В, то и событие В не зависитот события А. Такие события называются независимыми. Аналогично, если событие А зависитот события В, то и событие В зависитот события А. В этом случае события называются зависимыми.
. В противном случае событие А называется зависимым от события В. Нетрудно показать, что если событие А не зависитот события В, то и событие В не зависитот события А. Такие события называются независимыми. Аналогично, если событие А зависитот события В, то и событие В зависитот события А. В этом случае события называются зависимыми.
Вероятность произведения двух независимых событий равна произведению их вероятностей:
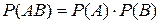 (11)
(11)
Задание 5. Для сигнализации о пожаре установлены два независимо работающих датчика. Вероятности того, что при пожаре датчик сработает, для 1-го и 2-го датчиков соответственно равны 0,8 и 0,9.
а) Найти вероятности следующих событий:
1) А - сработают оба датчика;
2) В - сработает только первый датчик;
3) С - сработает только один датчик;
4) D - сработает хотя бы один датчик.
б) Известно, что сработал только один датчик. Найти вероятность того, что это был первый.
Решение. а) Введем события: А 1 – 1-ый датчик сработает; А 2 – 2-ой датчик сработает. Тогда 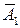 и
и 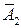 - противоположные события (датчики не сработают). По условию P (А 1)=0,8; P (А 2)=0,9. Вероятности противоположных событий найдем по формуле (7):
- противоположные события (датчики не сработают). По условию P (А 1)=0,8; P (А 2)=0,9. Вероятности противоположных событий найдем по формуле (7): 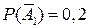 ;
; 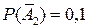 .
.
|
|
|
1) Событие А заключается в том, что сработали оба датчика, т.е. 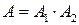 . События А 1 и А 2 по условию задачи независимы, поэтому по формуле (11) имеем:
. События А 1 и А 2 по условию задачи независимы, поэтому по формуле (11) имеем: 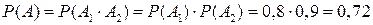 .
.
2) Событие В заключается в том, что сработает только первый датчик, т.е. 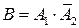 . Тогда
. Тогда 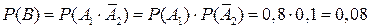 .
.
3) Событие С заключается в том, что сработает только один датчик – либо только 1-ый, либо только 2-ой. В этом случае событие С представляет собой сумму двух несовместных событий: 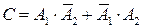 . С учетом формул (5) и (11) имеем:
. С учетом формул (5) и (11) имеем: 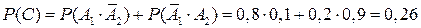 .
.
4) Событие D заключается в том, что сработает хотя бы один датчик, т.е. 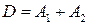 . События А 1 и А 2 совместны, поэтому для вычисления вероятности события D необходимо воспользоваться формулой (8):
. События А 1 и А 2 совместны, поэтому для вычисления вероятности события D необходимо воспользоваться формулой (8):
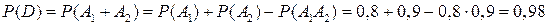 .
.
Отметим, что вероятность события D можно найти и другим способом. Рассмотрим противоположное событие 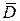 - ни один датчик не сработал. Очевидно, что
- ни один датчик не сработал. Очевидно, что 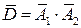 и
и 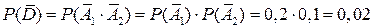 . Тогда по формуле (7) имеем:
. Тогда по формуле (7) имеем: 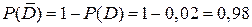 .
.
б) Для решения данной задачи необходимо найти вероятность 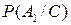 . По формуле (9) имеем:
. По формуле (9) имеем: 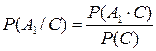 . Произведение
. Произведение 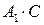 означает, что одновременно произошли два события - А 1 (1-ый датчик сработал) и С (сработал только один датчик). Следовательно,
означает, что одновременно произошли два события - А 1 (1-ый датчик сработал) и С (сработал только один датчик). Следовательно, 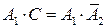 , и
, и 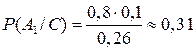 .
.
 2015-04-01
2015-04-01 1564
1564








