Если случайные величины X и Y связаны линейной корреляционной зависимостью, то уравнение регрессии Y на X 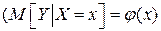 - т.е. условное математическое ожидание случайной величины Y является функцией от х, и эта функция
- т.е. условное математическое ожидание случайной величины Y является функцией от х, и эта функция 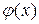 - линейная) имеет вид:
- линейная) имеет вид: 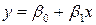 .
.
Аналогично уравнение регрессии Х на Y или прямая регрессия Х на Y есть: 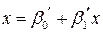 .
.
Коэффициенты уравнений регрессии находят методом наименьших квадратов, то есть из условия, что сумма квадратов отклонений возможных значений случайной величины от теоретических значений (рассчитанных по уравнению регрессии) имеет минимум при данных значениях коэффициентов уравнения регрессии. Полученные этим методом коэффициенты имеют вид:
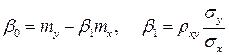 .
. 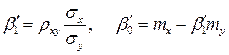 ,
,
здесь 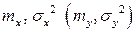 - математическое ожидание и дисперсия случайной величины
- математическое ожидание и дисперсия случайной величины 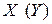 ,
,
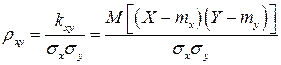 - коэффициент корреляции между случайными величинами
- коэффициент корреляции между случайными величинами 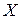 и
и 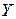 (
(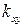 - корреляционный момент (ковариация)).
- корреляционный момент (ковариация)).
Пусть в результате эксперимента получена выборка 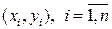 . Предварительное представление о зависимости между Х и Y можно получить, отмечая элементы выборки
. Предварительное представление о зависимости между Х и Y можно получить, отмечая элементы выборки 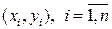 в виде точек на плоскости с выбранной системой координат. Такое представление выборки системы двух случайных величин называется диаграммой рассеивания.
в виде точек на плоскости с выбранной системой координат. Такое представление выборки системы двух случайных величин называется диаграммой рассеивания.
|
|
|
Если есть основания предполагать, что существует линейная корреляционная зависимость между Х и Y, то можно решить следующие задачи статистики.
Задача 1. Точечные оценки математических ожиданий, дисперсий, ковариации, коэффициента корреляции и коэффициентов уравнений регрессии: 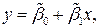
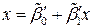 можно рассчитать по формулам:
можно рассчитать по формулам:
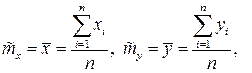
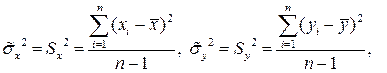
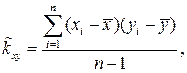
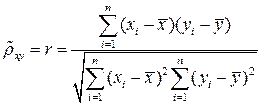 ,
,
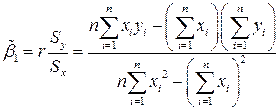 ,
, 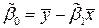 ,
,
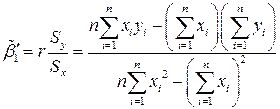 ,
, 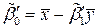 .
.
Для контроля правильности вычислений используют соотношение
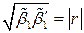 .
.
Задача 2. Для построения доверительного интервала для коэффициента корреляции 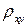 можно воспользоваться тем обстоятельством, что статистика
можно воспользоваться тем обстоятельством, что статистика 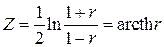 имеет приближенно нормальное распределение с математическим ожиданием
имеет приближенно нормальное распределение с математическим ожиданием 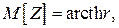 и дисперсией
и дисперсией 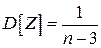 при сравнительно небольших объемах выборки
при сравнительно небольших объемах выборки 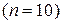 . Тогда доверительный интервал для
. Тогда доверительный интервал для 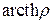 при уровне значимости
при уровне значимости 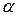 (
(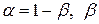 - доверительная вероятность) будет
- доверительная вероятность) будет 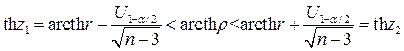 , здесь
, здесь 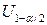 - квантиль порядка
- квантиль порядка 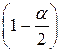 нормального распределения. Доверительный интервал для коэффициента корреляции
нормального распределения. Доверительный интервал для коэффициента корреляции 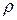 вычисляют с помощью таблиц гиперболического тангенса
вычисляют с помощью таблиц гиперболического тангенса 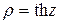 , то есть
, то есть 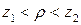 .
.
Задача 3. При проверке статистической гипотезы 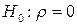 , т.е. гипотезы о том, что нормально распределенные случайные величины Х и Y некоррелированы, используют статистику
, т.е. гипотезы о том, что нормально распределенные случайные величины Х и Y некоррелированы, используют статистику 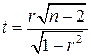 , которая имеет распределение Стьюдента с
, которая имеет распределение Стьюдента с 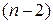 степенями свободы. Если окажется, что
степенями свободы. Если окажется, что 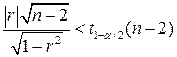 , то гипотезу
, то гипотезу 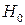 принимают при уровне значимости
принимают при уровне значимости 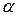 .
.
 2015-04-01
2015-04-01 775
775







