Контрольная работа № 7. Задания

1.Записать комплексное число 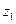в трех формах записи. Вычислить: 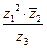. Найти все значения корня: 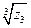(таблица 1).

2. Вычислить интегралы от функций комплексного переменного (таблица 2).

3. Исследовать сходимость положительных числовых рядов (таблица 3).

4. Разложить функцию в ряд по степеням 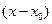. Найти радиус и область сходимости ряда (табдица 4).

5. Разложить функцию в ряд Фурье (таблица 5).

Пример выполнения контрольной работы № 1. Вариант 0.

1. Записать комплексное число 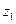в трех формах записи. Вычислить: 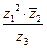. Найти все значения корня: : .

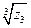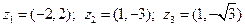Решение. Рассмотрим число 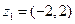- это общая форма комплексного числа. Тогда это число можно изобразить точкой на комплексной плоскости (или радиус-вектором). Запишем его в трех других формах. Для этого вычислим модуль и главное значение аргумента данного числа (модуль комплексного числа – есть расстояние от этой точки до начала координат (или длина радиус-вектора), а аргумент – есть угол между положительным направлением оси 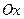и радиус-вектором точки (отсчет против часой стрелки). Аргумент вычисляется с точностью до 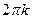, поэтому выделяют главное значение аргумента):

,

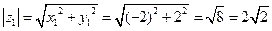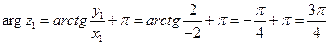(т.к. ).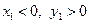

Тогда: 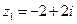- алгебраическая форма записи числа;

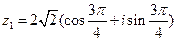- тригонометрическая форма записи числа;

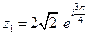- показательная форма записи числа.

Вычислим теперь значение выражения: .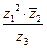

Для этого воспользуемся алгебраической формой комплексных чисел:

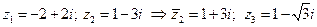. Имеем:

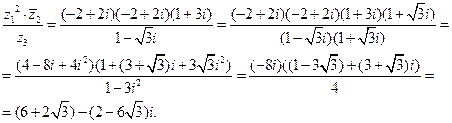
Для того, чтобы найти все значения корня из комплексного числа удобно записать его в тригонометрической форме. Сначала найдем модуль и аргумент числа 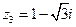. Получим: .

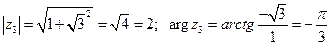Используем формулу извлечения корня из комплексного числа:

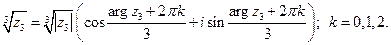
Подставим найденные значения:

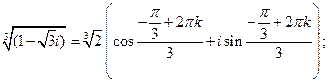
Подставляя 3 значения 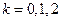, окончательно получаем 3 значения корня: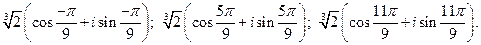

Ответ. ; ;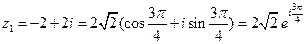

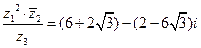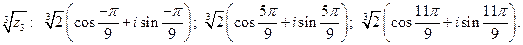
2. Вычислить интегралы от функций комплексного переменного.

а) 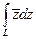, где L – линия, соединяющая точк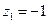и и .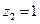

Решение. Так как подынтегральная функция 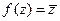не является аналитической, то используем общую формулу сведения интеграла от комплексной функции к криволинейным интегралам от вещественных функций: .

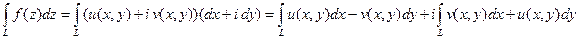Для комплексного числа 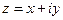сопряженным является число 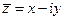, тогда для функции 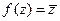имеем: 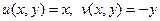. Кривая 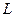- есть отрезок, соединяющий точк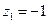и и 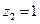, уравнение этой кривой: 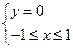. Тогда вдоль этой криво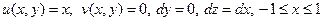й: и:

= .

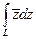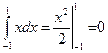б) Использовать интегральную формулу Коши: ,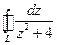

L – окружность: .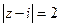

Решение. Рассмотрим подынтегральную функцию 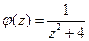. Ее особые точки (в которых знаменатель обращается в 0) 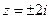. Одна из них 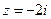не принадлежат области, охватываемой кривой L, а вторая 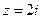принадлежит этой области (см. Рис.10), поэтому в этой области функция 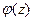не является аналитической.

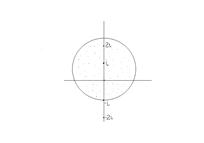
Рис. 10

Интеграл можно переписать в виде: 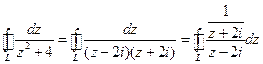, при этом функция, стоящая в числителе: 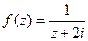, аналитическая в области, ограниченной контуром L, и точка 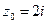охватывается контуром L. Применяя интегральную формулу Коши: 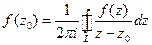, получаем:

.

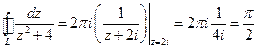Ответ. а) 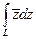=0; б) .

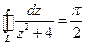3. Исследовать сходимость положительных числовых рядов.

Решение. а) 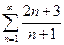.Общий член данного ряда: 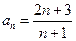. Для исследования сходимости, сначала проверяем выполнение необходимого признака сходимости. 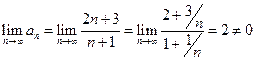; необходимый признак не выполняется, значит, ряд расходится.

б) 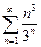. Общий член данного ряда 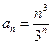. Проверим выполнение необходимого признака сходимости: 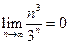, значит, данный ряд может сходиться и расходиться. Применим достаточный признак сходимости, воспользуемся признаком Даламбера: 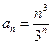, , 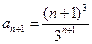тогда 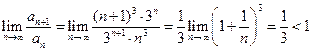. Следовательно, данный ряд сходится.

Ответ. Ряд 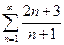расходится; ряд 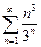сходится.

4. Разложить функцию 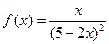в ряд по степеням 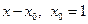. Найти радиус и область сходимости ряда.