Определение 8.3. Уравнения, содержащие тригонометрические функции, называются тригонометрическими.
Рассмотрим первоначально основные виды и способы решения простейших тригонометрических уравнений.
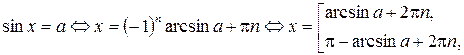 ,
, 
 ,
, 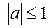 .
.
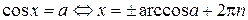 ,
, 
 ,
, 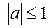 .
.
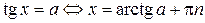 ,
, 
 ,
, 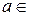
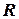 .
.
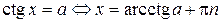 ,
, 
 ,
, 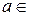
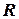 .
.
Пример 8.10. Решить уравнение 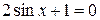 .
.
Решение.
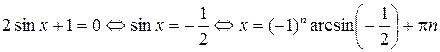 ,
, 


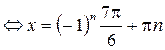 ,
, 
 .
.
Ответ: 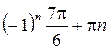 ,
, 
 .
.
Пример 8.11. Решить уравнение 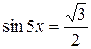 .
.
Решение. 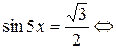
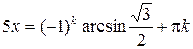 ,
, 


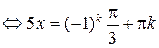 ,
, 


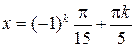 ,
, 
 .
.
Ответ: 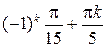 ,
, 
 .
.
Пример 8.12. Решить уравнение 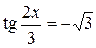 .
.
Решение. 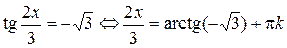 ,
, 


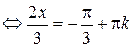 ,
, 


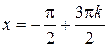 ,
, 
 .
.
Ответ: 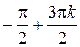 ,
, 
 .
.
Пример 8.13. Решить уравнение 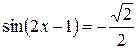 .
.
Решение. 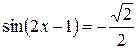
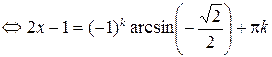 ,
, 


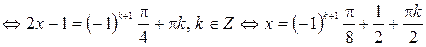 ,
, 
 .
.
Ответ: 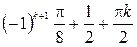 ,
, 
 .
.
Пример 8.14. Решить уравнение 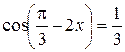 .
.
Решение. Воспользуемся четностью функции 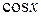 , тогда
, тогда
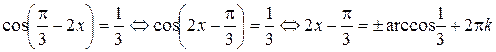 ,
, 


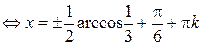 ,
, 
 .
.
Ответ: 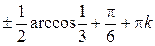 ,
, 
 .
.
Пример 8.15. Решить уравнение 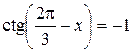 .
.
Решение. Учитывая нечетность функции 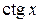 , имеем
, имеем
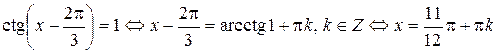 ,
, 
 .
.
Ответ: 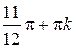 ,
, 
 .
.
Если уравнение не является простейшим, то с помощью тождественных преобразований его нужно привести к одному или нескольким простейшим. Отметим, что не существует единого алгоритма решения тригонометрических уравнений. Выделим некоторые методы решения тригонометрических уравнений.
1. Разложение на множители.
2. Однородные уравнения.
|
|
|
Определение 8.4. Однородными тригонометрическими уравнениями 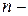 й степени относительно
й степени относительно 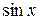 и
и 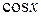 называются уравнения вида:
называются уравнения вида:
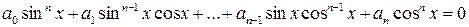 , ,
| (8.3) |
где 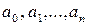 - действительные числа,
- действительные числа, 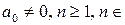
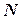 . Сумма показателей степени при
. Сумма показателей степени при 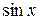 и
и 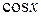 у всех слагаемых уравнений равна
у всех слагаемых уравнений равна 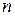 .
.
Замечание 8.1. Отметим, что 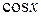 не может быть равен нулю, так как при
не может быть равен нулю, так как при 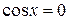 исходное уравнение примет вид:
исходное уравнение примет вид: 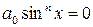 , откуда
, откуда 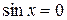 , что невозможно, поскольку
, что невозможно, поскольку 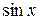 и
и 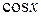 не могут равняться нулю одновременно.
не могут равняться нулю одновременно.
Разделим уравнение (8.3) на 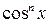 , тогда имеем
, тогда имеем
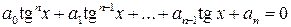 , ,
| (8.4) |
В (8.4) сделаем замену 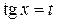 , тогда получим алгебраическое уравнение
, тогда получим алгебраическое уравнение
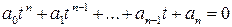 .
.
3. Введение вспомогательного аргумента (при этом используются формулы (8.1), (8.2)).
4. Метод оценки левой и правой части. Такие уравнения решаются путем сведения к системе тригонометрических уравнений.
5. Использование формул понижения степени (формул половинного аргумента).
Пример 8.16. Решить уравнение 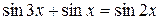 .
.
Решение. 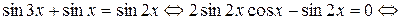
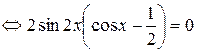
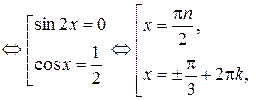
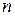 ,
, 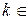
 .
.
Ответ:  ;
; 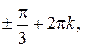
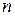 ,
, 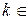
 .
.
Пример 8.17. Решить уравнение 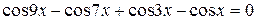 .
.
Решение. 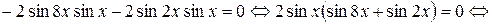
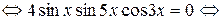
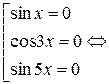
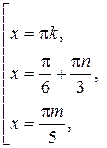
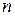 ,
, 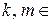
 .
.
Так как при 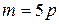 ,
, 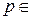
 , решения первого и третьего уравнения совокупности совпадают, то получаем:
, решения первого и третьего уравнения совокупности совпадают, то получаем: 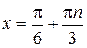 ,
, 
 и
и 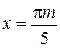 ,
, 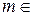
 .
.
Ответ: 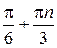 ;
; 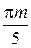 ,
, 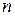 ,
, 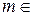
 .
.
Пример 8.18. Решить уравнение
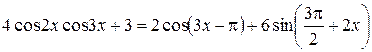 .
.
Решение. Используя четность функции 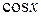 и формулы приведения, получаем
и формулы приведения, получаем
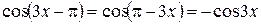 ,
, 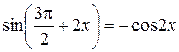 .
.
Тогда исходное уравнения примет вид:
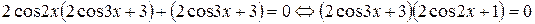 .
.
Так как 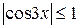 , то
, то 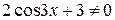 . Тогда из последнего уравнения имеем:
. Тогда из последнего уравнения имеем:
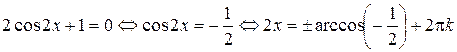 ,
, 


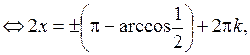



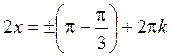 ,
, 



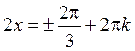 ,
, 


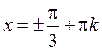 ,
, 
 .
.
Ответ: 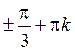 ,
, 
 .
.
Пример 8.19. Решить уравнение 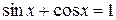 .
.
 2015-04-01
2015-04-01 300
300








