(1) (C)'=0 (2) (х n)'=nxn 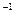
(3) (x)'=1 (4) (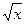 )'=
)'= 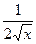
(5) (sinx)'= cosx (6) (cosx)'=- sinx
(7) (tgx)'= 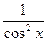 (8) (ctgx)'=-
(8) (ctgx)'=- 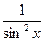
(9) (a 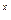 )'= a
)'= a 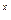 lna (10) (e
lna (10) (e 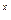 )'= e
)'= e 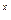
(11) (log 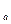 x)'=
x)'= 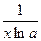 (12) (lnx)'=
(12) (lnx)'= 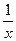
(13) (u ±υ)'= u'± υ' (14) (uυ)'= u ' υ + uυ '
(15) (Cu)'= Cu' (16) 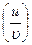 '=
'= 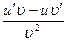
Если у = f (x), а u = φ (x), то f (u) называется функцией от функции (или сложной функцией от (х)). Тогда справедливо следующее правило дифференцирования функции:
(17) 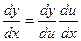 , или у '= ƒ (u) u '
, или у '= ƒ (u) u '
Пример 1. Найти производные функции:
а) у =5,6;
б) у = tg (π/4);
в) у=ln 2.
Р е ш е н и е. Используя формулу (1), имеем
а) (5,6)'=0;
б) (tg (π/4)'=0;
в) (ln2)'=0.
Пример 2. Найти производные функции:
а) у = х 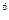 ;
;
б) у = 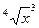 ;
;
в) у = х 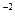 .
.
Р е ш е н и е. Используя формулу (2), получим:
а) (х 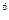 )'=6 х
)'=6 х 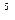 ;
;
б) 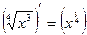 '=
'= 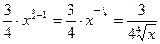 ;
;
в) 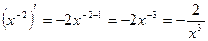 .
.
Пример 3. Найти производные функций:
а) ƒ (t)= 9t 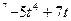 ;
;
б) ƒ (х)= 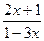 ;
;
в) ƒ (х)=(2х-3) (3х+1);
Р е ш е н и е. а) Используя формулы (13), (3), (15) и (2) находим:
а) ƒ '(t)=(9t 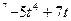 )' = (9t
)' = (9t 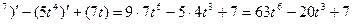 ;
;
б) По формуле (16) получаем:
ƒ '(х)= 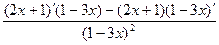 ;
;
Используя формулы (13), (15) и (3) находим:
ƒ' (х)= 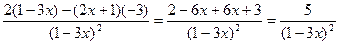
в) По формуле (14) имеем ƒ' (х)=(2х-3)'(3х+1)+(2х-3)(3х+1)'
Используя формулы (13), (15) и (3), находим:
ƒ'(х) = 2(3х +1) + (2х -3)3 = 6х + 2 + 6х -9 =12х -7.
Пример 4. Продифференцировать функцию ƒ (х)=(1-х 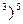 .
.
|
|
|
Р е ш е н и е. По формуле (17) получаем
f'(x)=5(1-x 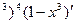
По формулам (13), (1) и (2) находим
f'(x)=5(1-х 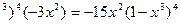 .
.
Частный случаи формулы (17):
(18) (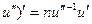 . (19) (sin u)' = cos u·u'
. (19) (sin u)' = cos u·u'
(20) ( cos u)'=- sin u · u ' (21) (tgu)'= 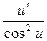 .
.
(22) (ctg u)'=- 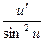 23) (
23) (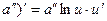 .
.
(24) (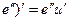 . (25) (log
. (25) (log 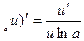
(26) (ln u)'= 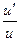
Пример 5. Найти производную функции y =ln(x 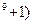 .
.
Р е ш е н и е. По формуле (26) находим y'= 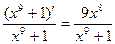
Пример 6. Найти производную функцию (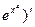 .
.
Р е ш е н и е. По формуле (24) получим
(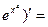
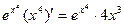
Пример 7. Найти производную функции:
а) y =cos(x 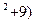 ;
;
б) y = tg (4 x -5);
в) y =ln sin3 x.
Р е ш е н и е.
а) (cos(x 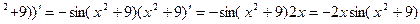
(использована формула (20));
б) (tg(4x-5))'= 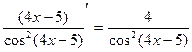 (использована формула (21);
(использована формула (21);
в) (ln sin3x)'= 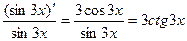 (использованы формулы (26) и (19)).
(использованы формулы (26) и (19)).
Пример 8. Найти производную функции:
а) y =cos x 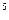 ;
;
б) y =ctg 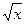 .
.
Р е ш е н и е.
а) (cos x 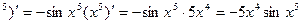 (использована формула (20));
(использована формула (20));
б) (ctg 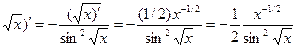
(использована формула (22)).
Пример 9. Найти производную функции f (x)= 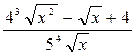 .
.
Р е ш е н и е. Представим корни в виде степеней и разделим почленно числитель дроби на знаменатель:
f (x) = 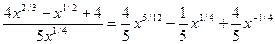
Дифференцируя, имеем
f '(x)= 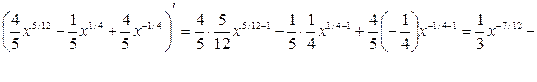 -
- 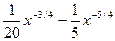
Пример 10. Дана функция f (x)= sin 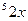 . Найти ƒ' (π/6).
. Найти ƒ' (π/6).
Р е ш е н и е. Данная функция является степенной (sin2 x) 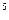 . По формуле (18) находим
. По формуле (18) находим 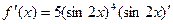 . Затем по формуле (19) получим
. Затем по формуле (19) получим
f ' (x)=5(sin 2 x) 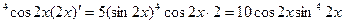
Вычислим значение найденной производной при x = π /6:
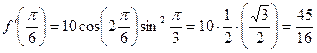 .
.
Пример 11. Найти производную функцию y= ln 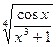
Р е ш е н и е.Предварительно прологарифмировав, получим
y = 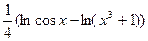 .
.
Продифференцируем полученную функцию, используя формулы (26), (6), (2), (15):
y '= 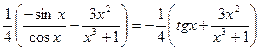
Пример 12. Решить уравнение ƒ '(x)=g'(x)+2 x, если ƒ (x)= 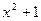 , а g(x)=
, а g(x)= 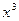 .
.
Р е ш е н и е. Найдем производные функции f (x)= x 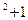 и g (x)= x
и g (x)= x 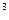 :
:
f ' (x)=2 x; g'(x)=3 x 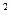 .
.
Представим найденные значения этих производных в заданное уравнение. После этой подстановки оно примет вид
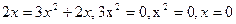
Ответ: х=0
Пример 13. Решить уравнение ƒ '(x)- ƒ (x)=0, если f (x)= x 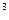 .
.
|
|
|
Р е ш е н и е. Найдем производную функции ƒ '(х)= х 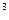 , f ' (x)=3 x
, f ' (x)=3 x 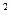 . Подставим саму функцию и её производную в заданное уравнение и решим его:
. Подставим саму функцию и её производную в заданное уравнение и решим его:
3 х 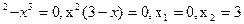
Ответ: 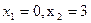 .
.
Пример 14. Решить уравнение 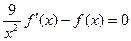 , если
, если 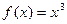 .
.
Р е ш е н и е. Подставляем функцию 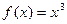 и её производную
и её производную 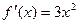 в заданное уравнение:
в заданное уравнение: 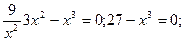
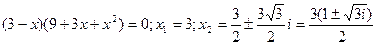 .
.
§2. Приложение производной.
Геометрические приложения: Пусть кривая L является графиком непрерывной функции у = f (x). Рассматриваем на кривой точку М (х 0; у 0)
 y и проведем касательную к графику функции
y и проведем касательную к графику функции

 в этой точке. Значение производной функции
в этой точке. Значение производной функции


 y0 M(x0-y0) y = f (x) у = f (x) в точке х0 равно угловому коэффициенту
y0 M(x0-y0) y = f (x) у = f (x) в точке х0 равно угловому коэффициенту
k касательной, проведенной к графику функции
в точке М (х 0; у 0), т.е. f' (x0)= k. Угловой
коэффициент k равен тангенсу угла наклона
 0 x0 х касательной с положительным направлением оси Ох.
0 x0 х касательной с положительным направлением оси Ох.
Уравнение касательной к графику функции у = f (x), проходящей через точку М (х 0; у 0), имеет вид
y - f (x 0)- f' (x 0)(x - x0)
Пример 1. Найти угловой коэффициент касательной, проведенной к параболе y =2 x 2 в точке, абсцисса которой равна единице.
Р е ш е н и е. Для вычисления углового коэффициента касательной найдем производную функции y =2 x 2 и вычислим её значение при х =1:
y' =(2 x 2)'=4 x; y' (1)=4·1=4; k = y '(1)=4
Пример 2. Найти угол наклона касательной к оси Ох и уравнение касательной к параболе у = х 2- х +1 в точке с абсциссой х0=-1.
Р е ш е н и е. Для вычисления угла наклона касательной найдем значение производной данной функции в точке абсциссой х 0=-1:
y'= (x 2 – x + 1)' = 2 x -1; y' (-1) = 2·(-1) -1 = -3
Находим угол наклона касательной к оси Ох:
k = y ' (- 1) = tga = - 3, откуда а = 108º26'
Уравнение касательной в точке с абсциссой х 0 имеет вид
y = f (x 0) = f' (x 0)(x - x 0).
Найдем значение функции в точке х 0=-1:
f (-1) =(-1)2 - (-1) + 1 =3
Подставив значение f (-1)=(-1)1(-1) x0=-1 в уравнении касательной,
получим y – 3= (-3) (x -(-1)); у = -3 х.
Физические приложения.
Пример 1. Скорость тела, движущегося прямолинейно, выражается законом υ(1)=3t + 6t2. Какое ускорение будет иметь тело через 5с после начала движения?
Р е ш е н и е. Известно, что α(t)=υ΄(t). Находим α(t)=υ ́(t)=3 +12t; при t=5 получим α(5)=3 + 12·5=63 (м/с2).
Пример 2. Тело движения прямолинейно по закону s(t)=5+4t+t2. Найти его скорость и ускорение в момент времени t=1с.
Р е ш е н и е. Известно, что 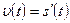 . Находим
. Находим 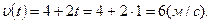 Зная, что
Зная, что 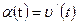 , находим
, находим 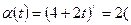 м/с2), откуда
м/с2), откуда 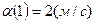 .
.
§3. Приложения производной к исследованию функции и построению графиков.
Пример. Исследовать функцию 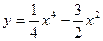 и построить её график.
и построить её график.
Р е ш е н и е.
- Область определения функции есть множество всех действительных чисел.
- Область изменения функций есть множество всех действительных чисел.
- Функция четная, так как
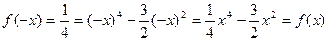 .
.
Значит, график функции симметричен относительно оси Оу.
4. Найдем производную
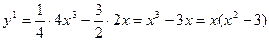 .
.
5. Находим критические точки функции, т.е. значения х, при которых у ΄́=0.
Имеем х (х 2-3)=0; х 1=0; х 2 – 3=0; х 2 =3; х 2,3=± 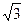 .
.
6. Вычислим значение функции в критических точках.
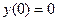 ;
; 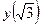 =-
=- 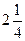 ;
; 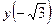 = -
= - 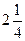 .
.
Составим таблицу:
| х | х < - 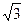
| - 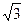
| - 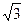 < х < 0 < х < 0
| 0 < х < 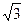
| 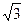
| 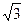 < х < х
| |
| у' | - | + | - | + | |||
| у | 
| 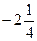
| 
| 
| 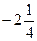
| 
| |
| min | max | min |
В первой строке таблицы указаны в порядке возрастания критические точки функции и ограниченные ими промежутки. Во второй строке отмечены
 у знаки производной в этих промежутках
у знаки производной в этих промежутках
(поскольку на каждом таком промежутке
 найти, определив знак производной в
найти, определив знак производной в
какой-либо точке рассматриваемого
промежутка). В третьей строке записаны - 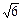 -
- 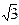
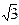
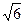 выводы о ходе изменения данной
выводы о ходе изменения данной

 0 х функции: -возрастает, - убывает
0 х функции: -возрастает, - убывает
а в четвертой – о виде критических точек.
- 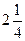
7. Находим точки пересечения с осью Ох. Полагая у =0, получим
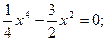
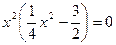 ;
; 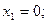
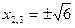 .
.
8. Строим график функции (см. выше)
Это построение удобно вести по промежуткам, которые приведены в таблице. Например, в таблице указано, что функция убывает на интервале
0< х < 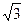 . Так данная функция непрерывна в точке 0 и
. Так данная функция непрерывна в точке 0 и 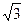 (будучи непрерывной всюду), то она убывает и на отрезке 0 < х <
(будучи непрерывной всюду), то она убывает и на отрезке 0 < х < 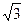 . Поэтому график убывает на этом отрезке от значения у (0)=0 до значения у (
. Поэтому график убывает на этом отрезке от значения у (0)=0 до значения у (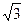 ) =-9/4. Аналогично строится график и на остальных промежутках.
) =-9/4. Аналогично строится график и на остальных промежутках.
|
|
|
Вопросы для самопроверки:
- Сформулируйте определение производной.
- В чём заключается геометрический смысл производной.
- Чему равна производная от постоянной величины.
- Сформулируйте правила дифференцирования суммы, произведения, частного двух функций.
- Сформулируйте правила дифференцирования сложной функции.
- Напишите формулы дифференцирования элементарных функций.
 2015-04-01
2015-04-01 758
758








