Теорема об исправляющем коде

Пусть при передаче кодовых слов происходит не более k ошибок.

Для того чтобы код являлся исправляющим все ошибки, число которых не более k, необходимо и достаточно чтобы наименьшее расстояние между кодовыми словами удовлетворяло неравенству:

d(b1, b2) ³ 2k+1.

Доказательство.

Достаточность. Пусть для любых двух слов b1 и b2 выполняется неравенство d(b1, b2) ³ 2k+1. Пусть при передаче слова b1 было принято слово c1, причём произошло не более k ошибок, т.е. d(b1, c1) £ k. Из неравенства треугольника следует: d(b1, c1) + d(c1, b2) ³ d(b1, b2) ³ 2k+1. Отсюда следует, что d(c1, b2) ³ 2k+1 - d(b1, c1) ³ k + 1, т.е. расстояние от с1 до любого другого кодового слова b2 больше чем k. Благодаря этому можно однозначно определить ближайшее к слову c1 кодовое слово b1, после чего декодировать его, т.е. исправить ошибку.

Необходимость. Доказательство от противного. Пусть минимальное расстояние между кодовыми словами меньше, чем 2k+1, т.е. найдутся два таких слова b1 и b2, что d(b1, b2) £ 2k. Пусть при передаче слова b1 получено слово c1, содержащее ровно k ошибок и расположеное на отрезке между b1 и b2.

Тогда d(b1, c1) = k, при этом d(b2, c1) = d(b1, b2) - d(b1, c1) £ k. Это означает, что по слову c1 нельзя однозначно восстановить, какое было передано кодовое слово - b1 или b2. Пришли к противоречию с условием, что код является исправляющим при условии, что имеется не более k ошибок при передаче.

Определение. Если для слов длины m в алфавите B={0, 1} используются кодовые слова длины n, то такие коды называются (m, n) – коды.

Для задания всех кодовых слов длины n можно их просто перечислить для каждого исходного передаваемого слова. Таких слов всего 2^m. Однако существует более удобный способ задания кодовых слов – матричный.

При матричном способе задания кодовых слов задаётся порождающая матрица G=|| g_ij ||, порядка m ´ n, каждый элемент которой принадлежит алфавиту B= {0, 1}. Кодовые слова b = b₁ b₂ b₃... b_m b_m+1 определяются для каждого заданного слова a = a₁ a₂ a₃... a_m умножением слова a слева, как вектора, на порождающую матрицу G:

b = aG,

причём b_j = (a₁g_1j + a₂g_2j + … a_mg_mj) mod 2.

Предыдущая формула означает, что суммирование a₁g_1j + a₂g_2j + … a_mg_mj ведётся по модулю 2, т.е. сначала вычисляется сумма в скобках, а затем вычисляется остаток от деления этой суммы на 2.

Пример 3. Рассмотрим порождающую матрицу

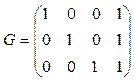
С помощью этой матрицы можно задавать (3, 4) - коды. Четвёртый символ кодовых слов будет контрольным: он будет равен 0, если исходное слово содержит чётное число единиц, и будет равен 1 в противном случае. Пусть задано слово a =101; его кодом будет b = aG = b₁ b₂ b₃ b₄ , где

b₁ = (1*1+0*0+1*0) mod 2 = 1;

b₂ = (1*0+0*1+1*0) mod 2 = 0;

b₃ = (1*0+0*0+1*1) mod 2 = 1;

b₄ = (1*1+0*1+1*1) mod 2 = 0;

т.е. кодовое слово b = 1010.

Для слова a =110 кодовым словом является слово b = 1100.

Пример 4. Рассмотрим порождающую матрицу G= (1, 1, 1, 1, 1). Её размерность 1 ´ 5. Поэтому она задаёт (1, 5) – код. Для слова a1 = 0 получим кодовое слово b1 = 00000; для слова a2 =1 получим b2 = 11111. Здесь минимальное расстояние между b1 и b2 равно 5, т.е. этот код может обнаружить четырёхкратную ошибку (5=k+1 при k=4) и исправить двукратную (5 = 2*k+1 при k=2).

Пример 5. Порождающая матрица

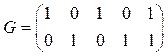
задаёт (2, 5) – код: a1=00 à b1 = 00000; a2=01 à b2 = 01011; a3=10 à b3 = 10101; a4=11 à b4 = 11110.

Кодовые слова, полученные методом матричного кодирования, образуют коммутативную группу по сложению. Это означает, что если b1 = a1*G и b2 = a2*G, то b1+ b2 = a1*G +a2*G = (a1+a2)*G.