Комбинаторные объекты

Тема 2. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

Цели и задачи изучения темы

В данной теме рассматриваются основы комбинаторики и алгоритмы порождения комбинаторных объектов.

Комбинаторные конфигурации

Аксиомы комбинаторики

Комбинаторика – один из разделов дискретной математики, который приобрел большое значение в связи с использованием его в теории вероятностей, математической логики, теории чисел, вычислительной технике, кибернетике.

Приведем пример простейшей комбинаторной задачи. Пусть из города А до города В можно добираться пароходом, поездом, автобусом, самолетом; из города В до города С – пароходом и автобусом. Сколькими способами можно осуществить путешествие по маршруту А – В – С?

Решение. Очевидно, число разных путей из А до С равно 4×2=8, так как, выбрав один из четырех возможных способов путешествия от А до В, имеем два возможных способа путешествия от В до С.

Исходя из этих соображений, сформулируем основное правило комбинаторики – правило произведения.

Правило произведения. Если некоторый выбор A можно осуществить m способами, а для каждого из этих способов некоторый другой выбор B можно осуществить n способами, то выбор “ A и B ” в указанном порядке можно осуществить m × n способами.

Это правило можно обобщить следующим образом.

Пусть требуется выполнить одно за другим k действий. Если первое действие выполнить n ₁ способами, второе действие – n ₂ способами, третье действие – n ₃ способами и так до k -го действия, которое можно выполнить n_k способами, то все k действий могут быть выполнены n ₁× n ₂× n ₃×…× n_k способами.

При подсчете числа различных комбинаций используется также правило суммы.

Правило суммы. Если некоторый выбор A можно осуществить m способами, а выбор B другими n способами, то выбор “либо A, либо B ” можно осуществить m+n способами.

Правило суммы также может быть обобщено на произвольное число действий.

Комбинаторные объекты

В разд.1.1.1 было дано понятие множества. Конечное множество S будем задавать списком его элементов: S= { s ₁, s ₂,…, s_n }, где s ₁, s ₂,…, s_n – элементы S (обязательно различные).

Введем понятие мультимножества. Мультимножество есть объединение не обязательно различных объектов. Его можно считать множеством, в котором каждому элементу поставлено в соответствие положительное целое число, называемое кратностью.

Конечное мультимножество S будем записывать в следующем виде:

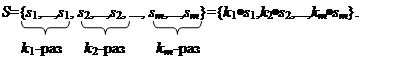Здесь все s_i различны и k_i – кратность элемента s_i. Тогда мощность S равна .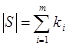

Теперь рассмотрим некоторые из комбинаторных объектов.

Подмножества. Множество M называется подмножеством множества S (обозначение М Ì S либо S É М; читается М входит в S, S содержит М) тогда и только тогда, когда любой элемент множества М принадлежит множеству S.

Теорема. Число подмножеств n -элементного множества S равно 2 ⁿ.

Доказательство. Поставим в соответствие каждому подмножеству M множества S двоичный набор длины n по следующему правилу: s_iÎМ, если и только если i -й разряд равен единице. Число двоичных наборов длины n, согласно правилу произведения, равно 2×2×…×2=2 ⁿ. Следовательно, число всех подмножеств n -элементного множества равно 2 ⁿ.

Перестановки. Перестановкой называется расположение элементов множества в определенном порядке.

Теорема. Число перестановок n -элементного множества S, т.е. число способов его упорядочивания выражается формулой P_n=n!.

Символом n! (читается n -факториал) обозначается произведение натуральных чисел от 1 до n: n!=1×2×...× n. Считается, что 0!=1.

Доказательство. Будем последовательно выбирать элементы множества S и располагать их в определенном порядке на n местах. На первое место можно поставить любой из n элементов. После того, как заполнено первое место, на второе место можно поставить любой из оставшихся n -1 элементов и т.д. Тогда по правилу произведения все n мест можно заполнить n ×(п -1)×(п -2)×...×2×1= n! способами. Следо­вательно, n -элементное множество можно упорядочить n!способами.

Размещения. Упорядоченные k -элементные подмножества множества из n элементов называются размещениями из n элементов по k.

Теорема. Число размещений из n по k определяется формулой:

.

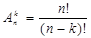Доказательство. Будем последовательно выбирать k -элементов из n -элементного множества, и располагать их в определенном порядке на k местах. На первое место можно поставить любой из n элементов, затем на второе - любой из n -1оставшихся и т.д. По правилу произ­ведения имеем

.

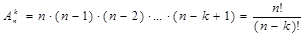Сочетания. Сочетанием из n элементов по k называется k -элементное подмножество множества из n элементов.

Теорема. Число сочетаний из n элементов по k выражается следу­ющей формулой:

.

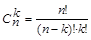Доказательство. Из n -элементного множества можно образовать 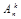различных упорядоченных k -элементных подмножеств. Каждое k -элементное подмножество может быть упорядочено Р_k способами. Тогда число сочетаний из n по k - число неупорядоченных k -элементных подмножеств n -элементного множества будет равно

.

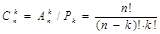Для числа сочетания справедливы равенства

,

,

.

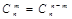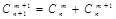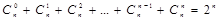Последнее свойство вытекает из теоремы о числе подмножеств конечного множества (объясните почему).

Перестановки с повторениями. Перестановкой с повторениями называется расположение элементов мультимножества в определенном порядке.

Теорема. Число перестановок с повторениями для мультимножества 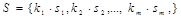выражается формулой

,

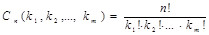где .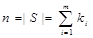

Доказательство 1. Рассмотрим одну перестановку мультимножества и заменим в ней все одинаковые элементы разными. Тогда, число различных перестановок, которые можно составить из рассматриваемой перестановки, равно k ₁!× k ₂!×…× k_m!. Проделав это для каждой перестановки, получим n! перестановок. Следовательно,

C_n (k ₁, k ₂,…, k_m)× k ₁!× k ₂!×…× k_m!= n!,

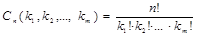
Число C_n (k ₁, k ₂,…, k_m) называется полиномиальным коэффициентом. Приведем еще одно доказательство данной теоремы.

Доказательство 2. Для упорядочивания мультимножества необходимо из n мест выбрать k ₁ мест для элемента s ₁, что можно сделать 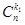способами, затем из n - k ₁ оставшиеся мест выбрать k ₂ мест для элемента s ₂, что можно сделать 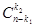способами и т.д. Тогда число способов упорядочивания мультимножества S по правилу произведения равно (напомнив, что 0!=1)

.

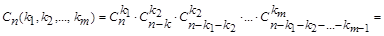
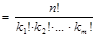Сочетания с повторениями. Сочетаниями из m элементов по n элементов с повторениями называются группы, содержащие n элементов, причем каждая элемент принадлежит к одному из m типов.

Пример. Из трех элементов (m =3) a, b, c можно составить такие сочетания по два с повторениями: aа, ab, ас, bb, bc, cc.

Теорема. Число различных сочетаний из m элементов по n с повторениями равно

.

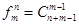Доказательство. Каждое сочетание полностью определяется, если указать, сколько элементов каждого из m типов в него входит. Поставим в соответствие каждому сочетанию последовательность нулей и единиц, составленную по следующему правилу: ставим подряд столько единиц, сколько элементов первого типа входит в сочетание, далее ставим нуль, и после него пишем столько единиц, сколько элементов второго типа содержит это сочетание и т.д. Например, написанным выше сочетаниям из трех букв по две будут соответствовать такие последовательности:

1100, 1010, 1001, 0110, 0101, 0011.

Таким образом, каждому сочетанию из m по n соответствует последовательность из n единиц и m -1 нулей. Число таких последовательностей равно числу способов, которыми можно выбрать m -1 мест для нулей из n + m -1 общего числа мест (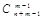), или то же самое числу способов выбора n мест для единиц из n + m -1мест (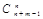). Равенство 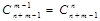следует из равенства .

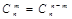Композиции и разбиения. Пусть стоит задача порождения разбиения положительного числа n в последовательность неотрицательных целых чисел { p ₁, p ₂,…, p_k }, так что p ₁ +p ₂+…+ p_k = n причем на р_i могут накладываться различные ограничения.

Если порядок чисел р_i важен, то (p ₁, p ₂,…, p_k) называется композицией n. Поиск композиций ведется с ограничением р_i >0.

Если k фиксировано, то такие композиции называются композициями n из k частей. При их поиске ограничение р_i >0 может сниматься, т.е. разрешается р_i =0.

Если порядок р_i не важен и р_i >0, то { p ₁, p ₂,…, p_k } является мультимножеством и называется разбиением n.

Поясним различие между композициями, композициями из k частей и разбиениями на следующем примере:

n =3,

композиции: (3), (1,2), (2,1), (1,1,1),

композиции из двух частей (р_i >0): (1,2), (2,1),

композиции из двух частей (р_i ³0): (0,3), (1,2), (2,1), (3,0),

разбиения: {3}, {1,2}, {1,1,1}.

Теорема. Число композиций n равно 2 ^{n -1}.

Доказательство. Разделим отрезок длины n на n отрезков единичной длины с помощью (n -1) точки. Тогда композиции n взаимно однозначно соответствует пометка некоторых из точек разделения. Элемен­тами композиции в этом случае будет расстояние между смежными точками. Например, композиция (2,2,1), n =5 представлена на рис.2.1.

Следовательно, каждая композиция n соответствует способу выбора подмножества из (n -1) точек. То есть число композиций n равно 2 ^n-1.

Теорема. Число композиций n из k частей с ограничением р_i >0 равно .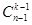

Доказательство. Представим композицию также как при доказательстве предыдущей теоремы. Каждая композиция n из k частей (р_i >0) соответствует способу выбора (k -1) - элементного подмножества точек из n -1 точек. То есть число таких композиций равно .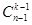

Теорема. Число композиций n из k частей, если p_i ³0 равно .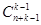

Доказательство. Каждой композиции n из k частей при р_i ³0 взаимно однозначно соответствует двоичный набор, такой, что первое слагаемое равно числу единиц, стоящих перед первым нулем в наборе, второе - числу единиц, стоящих перед первым и вторым нулями, и т.д. Пример такого представления композиции n =4, k =3 приведен в табл.2.1.

Длина набора равна n + k -1, число нулей равно k -1, следовательно, число наборов (искомых композиций) равно числу способов выбора k -1 мест для нулей из n + k -1 мест (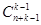) или тоже самое числу способов выбора n мест для единиц из n + k -1мест ().

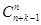Таблица 2.1

Иллюстрация к теореме о числе композиций n из k частей

№	Композиция	Двоичный набор	Сочетание из 6 по 2
	0+0+4	0 0 1 1 1 1	1 2
	0+1+З	0 1 0 1 1 1	1 3
	0+2+2	0 1 1 0 1 1	1 4
...	...	...	...
	3+0+1	1 1 1 0 0 1	4 5
	3+1+0	1 1 1 0 1 0	4 6
	4+0+0	1 1 1 1 0 0	5 6

Доказательство данной теоремы можно было также получить путем установки взаимно однозначного соответствия между данными композициями и множеством всех сочетания из k элементов по n с повторениями.