Суперпозиция сигнала и шума: распределение амплитуды и фазы

В реальных условиях прием сигнала, содержащего передаваемую информацию, всегда происходит на фоне шума. Шум может как приходить вместе с сигналом, так и генерироваться самой приемной станцией. Пусть I - мощность полезного сигнала, а s² - дисперсия фонового шума. Отношение сигнал/шум равно с/ш = I /s². Прием сигнала становится статистической задачей, если с/ш меньше или порядка единицы. В статистической теории приема сигналов выделяют две группы задач: 1) обнаружение сигнала на фоне шума; 2) выделение сигнала из шума. В первом случае требуется лишь с максимальной надежностью вынести статистическое решение о наличии или отсутствии сигнала. Сама структура сигнала не изучается. Во втором случае речь идет о наилучшем в статистическом смысле воспроизведении сигнала, скрытого в шуме. Пусть спектры сигнала и шума различны. Тогда решение обеих задач достигается посредством линейной фильтрации (сигнал и шум пропускают через линейный фильтр).

Решим первую задачу посредством построения оптимальноголинейногофильтра. Пусть на линейную систему действует регулярный сигнал

¥

z₀(t) = ò z₀(w) e^jwt dw (4.33)

- ¥

с произвольным спектром z₀(w), мгновенной интенсивностью: I₀(t) = z₀²(t), и

¥ ¥

энергией: Q₀ = ò I₀(t) dt = 2 p ò ïz₀(w)ï² dw (равенство Парсеваля [6]).

- ¥ - ¥

Пусть вместе с сигналом z₀(t) на вход фильтра поступает стационарный шум с нулевым средним значением и спектральной плотностью мощности G₀(w). Оптимальным называется фильтр, на выходе которого отношение с/ш наибольшее из всех возможных. Требуется найти передаточную функцию оптимального фильтра K(w). C учетом (4.33) выразим сигнал, его мощность и энергию на выходе фильтра

¥

z(t) = ò z₀(w) K(w) e^jwt dw, (4.34)

- ¥

¥

I(t) = (ò z₀(w) K(w) e^jwt dw)², (4.35)

- ¥

¥

Q = 2 p ò ïz₀(w) K(w)ï² dw. (4.36)

- ¥

Используя (4.3), находим отношение сигнал/шум на выходе фильтра

¥

(с/ш)_вых = I(t) / s²_вых = I(t) / ò ïK(w)ï² G₀(w)dw, (4.37)

- ¥

где s²_вых - дисперсия шума на выходе фильтра.

Интенсивность сигнала (4.35) оценим сверху с помощью неравенства Коши - Буняковского

¥ ¥

I(t) £ (ò ïz₀(w)ï² dw) (ò ï K(w)ï² dw). (4.38)

- ¥ - ¥

Предположим сначала, что шум на входе фильтра белый: G₀(w) = G₀ = =const. Подставляя (4.38) в (4.37) и учитывая (4.36), найдем

¥

(с/ш)_вых £ (1 /G₀) ò ïz₀(w)ï² dw = Q₀ / (2 p G₀). (4.39)

- ¥

Оптимальному фильтру соответствует знак равенства в (4.39) и в (4.38). Равенство достигается в момент времени t₀, если передаточная функция равна оптимальной

K(w) = K_опт(w) = a z₀*(w) exp (- j w t₀), (4.40)

где a и t₀ - произвольные постоянные, и знак «*» обозначает комплексное сопряжение.

Выражение (4.40) дает передаточную функцию оптимального фильтра, если входной шум белый. В (4.39) равенство достигается только в момент t = t₀, который оптимален для вынесения решения о наличии сигнала. Выражение (4.40) также показывает, что характеристика оптимального фильтра близка к спектру входного сигнала. Поэтому оптимальный фильтр называют также фильтром, согласованным с сигналом. Подставляя (4.40) в (4.34), найдем сигнал на выходе оптимального фильтра

¥

z(t) = a ò ïz₀(w)ï² exp (j w (t - t₀)) dw, (4.41)

- ¥

который принимает максимальное значение: z_max = a Q₀ / (2p), в момент t = t₀.

Сигнал (4.41) - симметричный относительно момента t = t₀ импульс, который по форме может сильно отличаться от сигнала на входе фильтра. Например, если на входе прямоугольный импульс, то на выходе - треугольный.

Теперь предположим, что шум на входе фильтра уже не является белым. Если спектры шума и сигнала на входе не перекрываются или перекрываются слабо, то нет необходимости строить оптимальный фильтр. Как обнаружение, так и выделение сигнала из шума достигается применением полосового фильтра. Сигнал находится в полосе пропускания фильтра, а шум - в полосе задержки. Более сложная ситуация, когда перекрытие сигнала и шума по спектру существенно или даже полное, но спектр шума значительно изменяется в полосе спектра сигнала. Оптимальный фильтр строят путем каскадного соединения двух фильтров. Передаточная функция всего фильтра: K(w) = K₁(w) K₂(w). Первый фильтр выбирают так, чтобы на его выходе шум был белым. Для этого задают

K₁(w) = C / G₀^1/2(w) exp (j j(w)), (4.42)

где выбор С = const и j(w) произволен.

Чтобы проверить, что на выходе первого фильтра действительно получается белый шум, достаточно подставить (4.42) в (4.5). Характеристику второго фильтра берут равной (4.40).

Перейдем к решению задачи о выделении сигнала из шума. Во многих случаях радиосигнал, например промодулированный человеческой речью, можно рассматривать как стационарный шум x₁(t). Предположим, что искажающая сигнал x₁(t) помеха x₂(t) - тоже стационарный шум. Пусть процессы x₁(t) и x₂(t) статистически независимы, < x₁ > = < x₂ > = 0, корреляционные функции B₁(t) и B₂(t) процессов x₁(t) и x₂(t) считаются известными. Требуется определить передаточную функцию K(w) фильтра, суммарный процесс на выходе которого

¥

x(t) = ò K(w) (x_1w + x_2w) e^jwt dw, (4.43)

- ¥

где спектральные компоненты (n = 1, 2)

¥

x_nw = ò x_n (t) e^-jwt dt, (4.44)

- ¥

с некоторой задержкой по времени t₀ наилучшим образом воспроизводил бы входной сигнал x₁(t).

В качестве критерия наилучшего воспроизведения выберем критерий минимума среднеквадратичного значения < m² > ошибки воспроизведения сигнала

m(t) = x(t + t₀) - x₁(t). (4.45)

Обозначим импульсную характеристику оптимального фильтра как H(q) и найдем уравнение, которому подчиняется эта функция. Используя интеграл наложения, запишем

¥

x(t) = ò H(q) (x₁(t - q) + x₂(t - q)) dq, (4.46)

- ¥

где функция: x₁(t - q) + x₂(t - q) - полный процесс на входе фильтра как функция аргумента t - q. Подставим (4.46) в (4.45) и выразим < m² >:

¥ ¥

<m²(t)>=òòH(q)H(q’)[B₁(q-q’)+B₂(q-q’)]dqdq’-2òH(q)B₁(q-t₀)dq+B₁(0), (4.47) - ¥ - ¥

где корреляционные функции: B₁(t) = < x₁ x_1t > и B₂(t) = < x₂ x_2t >.

Выражение (4.47) рассмотрим как функционал от функции H. Найдем вариацию этого функционала по Н:

¥ ¥

d<m²> = 2 ò dH(q) {ò H(q’)[B₁(q - q’) + B₂(q - q’)] dq’- B₁(q - t₀)}dq. (4.48)

- ¥ - ¥

Минимум функционала достигается при равенстве нулю его вариации

d<m²> = 0. (4.49)

Уравнения (4.48) и (4.49) совместны, если функция H(q) удовлетворяет

¥

ò H(q) [B₁(t - q) + B₂(t - q)] dq = B₁(t - t₀). (4.50)

- ¥

Уравнение (4.50) называется уравнениемВинера - Хопфа, и его решением является импульсная характеристика H(q) оптимального фильтра.

5.11. Тепловые шумы в электрических цепях. Формула Найквиста.

Тепловое движение свободных электронов в проводнике приводит к флуктуациям потоков электронов и вызывает случайный электрический ток i_T(t), который называют тепловым. Флуктуации электронной плотности, связанные с тепловыми токами, приводят к появлению случайной разности потенциалов на концах проводника. То есть любой двухполюсник, содержащий активное сопротивление, можно рассматривать как генератор случайной э.д.с. e_T(t). Тепловые шумы создают неустранимые флуктуационные помехи в любой радиосистеме. Применим термодинамический подход для выяснения спектральных свойств тепловых шумов. На рис. 4.4 показана цепь из двух двухполюсников с импедансами: z_{1, 2}(w) = R_{1, 2}(w) + j X_{1, 2}(w), помещенная в термостат при температуре T.

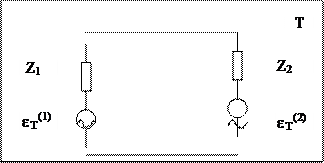
Рис. 1

Эквивалентная схема каждого из двух двухполюсников состоит из сопротивления и тепловой э.д.с. Пусть i_T^(к) - сила теплового тока, вызванного в цепи тепловой э.д.с. e_T^(к), где к = 1, 2. Полная сила шумового тока: i_T = i_T⁽¹⁾ + i_T⁽²⁾. Обозначим мощность, отдаваемую источником e_T⁽¹⁾ (e_T⁽²⁾) в двухполюсник z₂ (z₁), как P_{1, 2} (P_{2, 1}). Согласно второму началу термодинамики, теплообмен между отдельными частями равновесной изолированной системы не может нарушить теплового равновесия системы. Поэтому

P_{1, 2} = P_{2, 1}. (1)

Пусть G_T^(к)(w) - спектральная плотность мощности флуктуаций э.д.с. e_T^(к), где к = 1, 2. Полный импеданс цепи равен z = z₁ + z₂. Спектральная плотность мощности флуктуаций силы тока i_T^(к) равна G_T^(к)(w) / (zz­­­^*), где к = 1, 2, и знак «*» обозначает комплексное сопряжение. Тогда

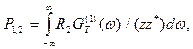(2)

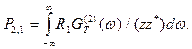(3)

Подставляя (2) и (3) в (1), получим

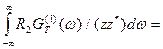
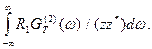(4)

Пусть, например, R₂ = 0 и R₁ > 0. Тогда из (4) следует: G_T⁽²⁾(w) = 0. То есть, если двухполюсник не содержит активного сопротивления, то спектральная плотность э.д.с. теплового шума на нем равна нулю. Пусть между двухполюсниками z₁ и z₂ включен дополнительно произвольный пассивный двухполюсник: z₃ = j X₃. Повторяя выкладки, вместо (4) получим

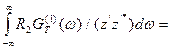
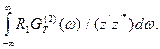, (5)

где z’ - полный импеданс цепи, z’ = z₁ + z₂ + z₃.

Так как выбор сопротивления z₃ произволен, то из (5) следует: R₂ G_T⁽¹⁾(w) / ïz’ï² = R₁G_T⁽²⁾(w) / ïz’ï². Отсюда следует, что отношение спектральной плотности теплового шума к активной части любого сопротивления, в котором он генерируется, является универсальной функцией Т и w:

G_T(w) = R(w) u(w, T) = Re {z(w)}u(w, T). (6)

Так как функция u(w, T) универсальна, то результат ее расчета не зависит от конкретного выбора системы. В классической области (при kT >> hn, где h - постоянная Планка, k - постоянная Больцмана, и частота: n = w/(2p)) справедлива теорема о равнораспределении энергии по степеням свободы. Тогда средняя энергия тепловых флуктуаций в системе с N колебательными степенями свободы равна

< w > = N k T. (7)

В качестве пробной системы рассмотрим высокодобротный колебательный контур (см. рис. 1), настроенный на резонансную частоту w₀ = 1 /(LC)^1/2. Под э.д.с. e(t) контура понимается тепловая э.д.с. e_T(t). Полоса пропускания контура: Dw = 2a = R/L, предполагается много уже эффективной ширины спектра флуктуаций G_T(w) тепловой э.д.с. Тогда входной шум можно аппроксимировать как белый: G_вх(w) = G_T(w₀). Передаточная функция изучаемой цепи: K(w) = w₀² /((w₀² - w²) + 2 j a w). Подставим приведенные выражения для G_T(w) и K(w) в (4.6). Найдем дисперсию флуктуаций напряжения на емкости контура: < u_вых²(t)> = p G_T(w₀) w₀² / (2a). Средняя энергия шумового электрического поля конденсатора: < w_E > = C < u_вых²(t)> /2, равна средней энергии шумового магнитного поля катушки индуктивности в контуре. Сумма этих энергий есть полная средняя энергия шумовых колебаний контура. Та же полная энергия может быть выражена из (7) при N = 1 (колебательный контур обладает одной колебательной степенью свободы). Таким образом, имеем: p CG_T(w₀) w₀² / (2a) = k T, то есть G_T(w₀) =kTR/p. Последнее выражение подставим в (6), взятое при w=w₀, и выразим оттуда универсальную функцию

u(w₀, T) = u(T) =(1 / p) k T. (8)

Из (8) следует, что искомая универсальная функция не зависит от частоты w.

Подставляя (8) в (6), получаем формулу Найквиста для спектральной плотности мощности теплового шума произвольного двухполюсника

G_T(w) = (k T/p) Re {z(w)}. (9)

Из (9) следует, что G_T(w)~T и что зависимость G_T(w) от частоты w полностью определяется зависимостью активной части сопротивления двухполюсника от частоты. Формула Найквиста справедлива в квазиклассическом приближении: kT>>hn (n=w/(2p)). При комнатной температуре: Т=300 К, равенство: kT=hn, имеет место приближенно на частоте n~10¹³ Гц. То есть классическое приближение при комнатной температуре справедливо для всего радиодиапазона частот. В частности, идеальное омическое сопротивление R не зависит от частоты. Поэтому тепловой шум, генерируемый омическим сопротивлением в радиодиапазоне, можно считать белым. Приближение d - коррелированности процесса хорошо выполняется практически для всех задач, связанных с изучением воздействия теплового шума на реальные радиотехнические системы.