Непрерывной функции на отрезке

Пусть функция у=f(x) определена в некотором промежутке множества Х и непрерывна в точке 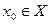. Тогда 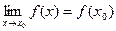, что означает: для любого 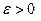, существует 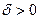, что для всех 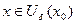выполняется неравенство .

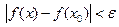Предположим теперь, что функция f(x) непрерывна на всем множестве Х, то есть непрерывна в каждой точке 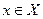. Пусть 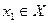, тогда функция f(x) непрерывна в этой точке, а по определению непрерывности это означает, что для любого 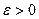, существует 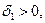что для всех 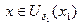выполняется неравенство 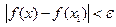. Возьмем другую точку 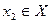, в ней функция тоже непрерывна, то есть для того же

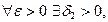
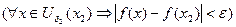и т.д.

Таким образом, для каждой точки 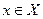в отдельности по заданному найдется своя δ_i -окрестность. Числа δ_i зависят не только от , но и от точек x_i.

Если бы множество Х было конечным, то мы смогли бы выбрать 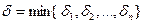такое, что оно подошло бы для всех рассматриваемых точек 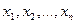. Но для бесконечного множества Х так рассуждать нельзя (из бесконечного множества { δ_i }нельзя выбрать наименьшее число).

Если для функции f(x), непрерывной в промежутке Х, по заданному найдется такое δ, которое подойдет для всех точек 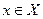, то эта функция будет равномерно непрерывной в х.

Опр. Функция y=f(x) называется равномерно непрерывной в промежутке Х, если для любого 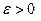, существует 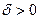, что для всех 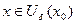выполняется неравенство 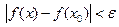, где бы в пределах рассматриваемого промежутка Х не лежали точки х₀ и х.

В этом случае число δ оказывается зависимым только от и не зависимым от выбора точки 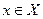. То есть δ годится для всех точек 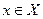одновременно.

Теорема Кантора:

Если функция f(x) определена и непрерывна на отрезке [ a, b ], то она и равномерно непрерывна на этом отрезке.

Теорема доказывается методом от противного (см. [3] ).

Из теоремы непосредственно вытекает такое следствие

Следствие: Пусть функция f(x) определена и непрерывна на отрезке [ a, b ]. Тогда по заданному 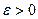найдется такое 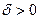, что если отрезок произвольно разбить на части с длинами, меньшими δ, то в каждом из них колебание функции f(x) будет меньше .

Замечание: Если функция f(x) при изменении х в каком-либо промежутке Х ограничена, то ее колебанием в этом промежутке называется разность w=M-m между ее точной верхней и нижней границами значений функции на Х. Если речь идет о непрерывной функции на отрезке [ a, b ], то колебанием будет попросту разность между наибольшим и наименьшим значениями функции в этом отрезке.

Доказательство следствия:

Действительно, если по заданному >0 в качестве δ взять число, о котором говорится в определении равномерной непрерывности, то в частичных отрезках с длинами, меньшими δ, разность между любыми двумя значениями функции будет по модулю меньше . В частности, это справедливо и относительно наибольшего и наименьшего из этих значений, разность которых и дает колебание функции в упомянутом частичном отрезке.