Завод производит два вида продукции: велосипеды и мотоциклы. При этом цех по сборке велосипедов имеет мощность 100 тыс. штук в год, цех по сборке мотоциклов — 30 тыс. Механические цеха завода оснащены взаимозаменяемым оборудованием, и одна группа цехов может производить либо детали для 120 тыс. велосипедов, либо детали для 40 тыс. мотоциклов, либо любую комбинацию деталей, ограниченную этими данными. Другая группа механических цехов может выпускать детали либо для 80 тыс. велосипедов, либо для 60 тыс. мотоциклов, либо любую допустимую их комбинацию. В результате реализации каждой тысячи велосипедов завод получает прибыль в 2 тыс. ден. ед., а каждой тысячи мотоциклов — 3 тыс. ден. ед. Найти такое сочетание объемов выпуска продукции, которое дает наибольшую сумму прибыли.
Найти оптимальный план выпуска велосипедов и мотоциклов по условиям.
Решение. В математической записи задача имеет вид:
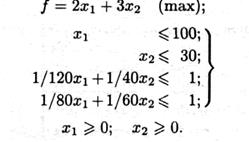
Областью допустимых решений системы линейных неравенств будет многоугольник OABCD (рис. 2.6). Вектор 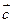 имеет координаты с1 =2, с2 = 3. (Поскольку вектор
имеет координаты с1 =2, с2 = 3. (Поскольку вектор 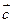 нам необходим лишь для выяснения направления, то, сообразуясь с масштабом чертежа, можно для большей наглядности построить вектор
нам необходим лишь для выяснения направления, то, сообразуясь с масштабом чертежа, можно для большей наглядности построить вектор 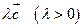 . В данном случае построен вектор 5
. В данном случае построен вектор 5 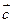 .
.
|
|
|
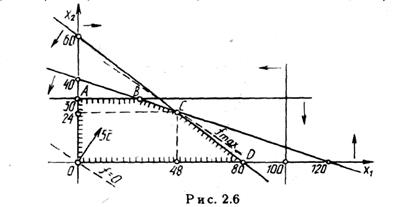
Параллельным перемещением вспомогательной прямой f = 0, перпендикулярной к вектору 5 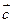 , находим точку С, в которой функция f достигает наибольшего значения. Решая совместно уравнения граничных прямых ВС и CD:
, находим точку С, в которой функция f достигает наибольшего значения. Решая совместно уравнения граничных прямых ВС и CD:
x1/120+ +x2/40 = 1 и x1/80 + x2/60 = 1,
находим координаты точки С: х1 = 48, х2 = 24; при этом fmax = 168.
Итак, выпускать следует 48 тыс. велосипедов и 24 тыс. мотоциклов; максимальная прибыль завода по этим видам продукции составит 168 тыс. ден. ед.
Задачи со многими переменными. Как указывалось, задачу со многими переменными можно решить графически, если в ее канонической записи присутствует не более двух свободных переменных, т.е. 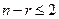 , где п — число переменных, r — ранг матрицы системы ограничительных уравнений задачи. Чтобы решить такую задачу, систему ограничительных уравнений надо преобразовать к разрешенному виду, т. е. выделить некоторый базис переменных. Затем базисные переменные следует опустить и перейти к эквивалентной системе неравенств. Целевая функция также должна быть выражена только через свободные переменные. Полученную двухмерную задачу решают обычным графическим методом. Найдя две координаты оптимального решения, подставляют их в ограничительные уравнения исходной задачи и определяют остальные координаты оптимального решения.
, где п — число переменных, r — ранг матрицы системы ограничительных уравнений задачи. Чтобы решить такую задачу, систему ограничительных уравнений надо преобразовать к разрешенному виду, т. е. выделить некоторый базис переменных. Затем базисные переменные следует опустить и перейти к эквивалентной системе неравенств. Целевая функция также должна быть выражена только через свободные переменные. Полученную двухмерную задачу решают обычным графическим методом. Найдя две координаты оптимального решения, подставляют их в ограничительные уравнения исходной задачи и определяют остальные координаты оптимального решения.
Решая графически полученную двухмерную задачу, следует помнить, что на каждой граничной прямой соответствующее неравенство обращается в равенство, поэтому опущенная при образовании этого неравенства базисная переменная равна нулю. В связи с этим в каждой из вершин области допустимых решений по крайней мере две переменные исходной задачи принимают нулевые значения.
|
|
|
Пример 2.. Найти оптимальный план ЗЛП, используя графический способ.
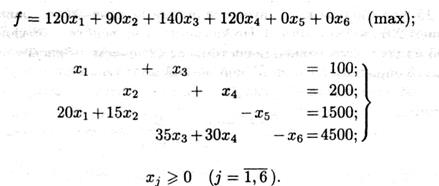
Решение. В системе ограничительных уравнений выделим какой-либо базис и убедимся, что число свободных переменных не превышает двух. Затем перейдем к эквивалентной системе неравенств.
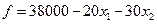 (max)
(max)
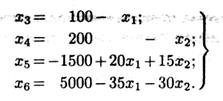
Опуская неотрицательные базисные переменные x3, x4, x5 и x6, приходим к двухмерной задаче, записанной в симметричной форме:
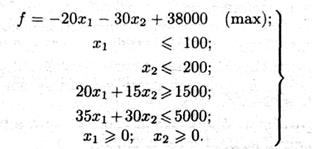
Решение задачи приведено на рис. 2.8. Напомним, что на каждой граничной прямой одна из переменных исходной задачи обращается в нуль. Так, неравенству 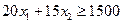 соответствует граничная прямая АВ с уравнением
соответствует граничная прямая АВ с уравнением 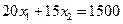 . Но указанное неравенство образовано из третьего уравнения системы путем отбрасывания переменной х5, следовательно, на прямой АВ х5 = 0.
. Но указанное неравенство образовано из третьего уравнения системы путем отбрасывания переменной х5, следовательно, на прямой АВ х5 = 0.
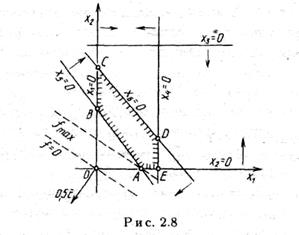
Из рис. 2.8 видно, что наибольшего значения функция f достигает в точке А пересечения прямых АВ и АЕ (х2 = 0), поэтому 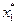 = 75,
= 75, 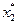 =0. Одновременно в этой вершине
=0. Одновременно в этой вершине 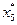 = 0. Значения других компонентов оптимального плана находим из уравнений
= 0. Значения других компонентов оптимального плана находим из уравнений 
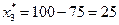 ,
, 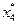 =200,
=200, 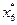 =2375; при этом fmax=36500.
=2375; при этом fmax=36500.
Задание.
Решить графически задачу линейного программирования.
Варианты:
1. 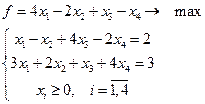
2. 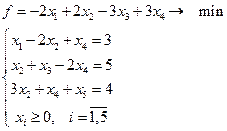
3. 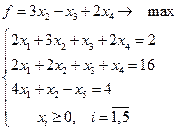
4. 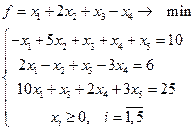
5. 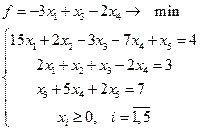
6. 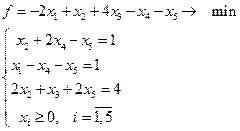
7. 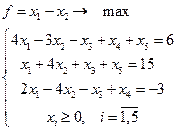
8. 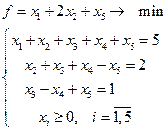
9. 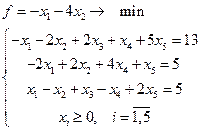
10. 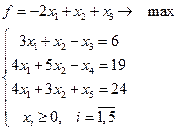
11. 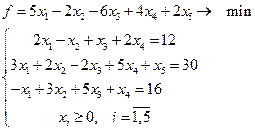
12. 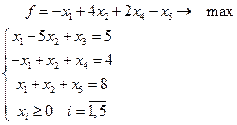
13. 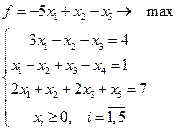
14. 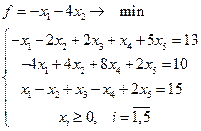
 2015-05-05
2015-05-05 3097
3097






