| Месяц | Продано магнитофонов, тыс.шт. | Трехуровневые скользящие суммы | Трехуровневые скользящие средние | Четырехуровневые скользящие суммы | Четырехуровневые скользящие средние нецентриро-ванные | Четырехуровневые скользящие средние центрированные |
| А | ||||||
| январь | - | - | - | - | ||
| февраль | ||||||
| 23,8 | ||||||
| март | - | 24,4 | ||||
| 25,0 | ||||||
| апрель | 24,9 | |||||
| 24,8 | ||||||
| май | 25,8 | |||||
| 26,8 | ||||||
| июнь | 27,0 | |||||
| 27,3 | ||||||
| июль | 27,5 | |||||
| 27,8 | ||||||
| август | 28,4 | |||||
| 29,0 | ||||||
| сентябрь | 29,3 | |||||
| 29,5 | ||||||
| октябрь | 30,1 | |||||
| 30,8 | ||||||
| ноябрь | - | |||||
| декабрь | - | - |
Недостаток метода простой скользящей средней состоит в том, что сглаженный ряд динамики сокращается ввиду невозможности получить сглаженные уровни для начала и конца ряда. Этот недостаток устраняется применением метода аналитического выравнивания для анализа основной тенденции.
Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени - у = f(t).
При таком подходе изменение явления связывают лишь с течением времени, считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени. Правильно построенная модель должна соответствовать характеру изменения тенденции исследуемого явления. Выбранная функция позволяет получить выровненные или теоретические значения уровней ряда динамики.
Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы разной степени, экспоненты, логистические кривые и другие виды.
Полиномы имеют следующий вид:
полином первой степени y¯t=a0+a1t
полином второй степени y¯t =a0+a1t + a2t2 (9.24.)
полином третьей степени y¯t =a0 +a1t + a2t2 +a3t3
полином n-ой степени y¯t =a0 +a1t + a2t2+...+antn
Здесь а0; a1; а2;... аn - параметры полиномов, t - условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, например, параметр а0 характеризует средние условия развития ряда динамики, параметр a1 - скорость роста, параметр а2 - ускорение роста, параметр аn - изменение ускорения.
Оценка параметров в моделях (9.24) находится методом наименьших квадратов. Как известно, суть его состоит в определении таких параметров (коэффициентов), при которых сумма квадратов отклонений расчетных значений уровней от фактических значений была бы минимальной. Таким образом, эти оценки находятся в результате минимизации выражения:
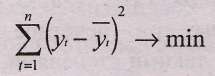 (9.25.)
(9.25.)
где yt - фактическое значение уровня ряда динамики; yt - расчетное значение; п – длина ряда динамики.
В результате минимизации выражения (9.25) получается система нормальных уравнений:
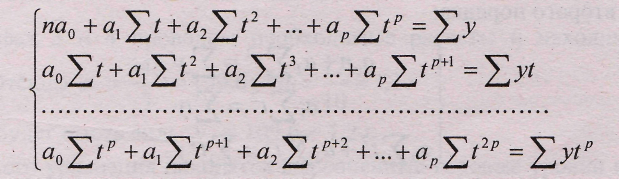 (9.26.)
(9.26.)
где n - число членов в ряду динамики, t=l,2,...,n
Система 9.26, состоящая из «р» уравнений, содержит в качестве известных величин ∑y, ∑yt,…,∑ytp, то есть суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 1,2,...,р и неизвестных величин aj. Решение этой системы относительно а0, ai,...,ap и дает искомые значения параметров.
Системы для расчета параметров полиномов невысоких степеней намного проще. Обозначим последовательные параметры полиномов как а0, a1, a2. Тогда системы нормальных уравнений для оценивания параметров прямой y¯t = а0 + a1t примет вид:
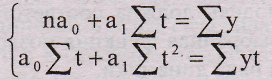 (9.27.)
(9.27.)
для параболы второго порядка (yt=a0+a1t+a2t2):
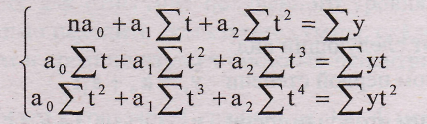 (9.28.)
(9.28.)
Составление нормальных уравнений можно упростить, воспользовавшись тем, что величины Yt, yt2 и т.д. не зависят от конкретных уровней ряда. Эти суммы являются функциями только числа членов в динамическом ряду. Для них получены следующие формулы:
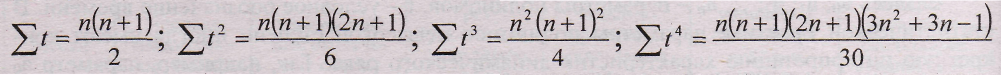
(суммирование по t = 1+п).
Другой подход к упрощению расчетов заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, а так же уменьшаются абсолютные значения величин, участвующих в расчете. Если до переноса начала координат t было равно 1,2,3,...,n, то после переноса:
• для нечетного числа уровней ряда t =...;-3;-2;-1; 0; 1; 2; 3;...
• для четного числа уровней ряда t =...;-5;-3;-1; 1; 3; 5;...
Следовательно, ∑t и все ∑tp, у которых «р» - нечетное число, равны 0. Таким образом, все члены уравнений, содержащие St с такими степенями, могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой:
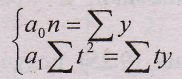 (9.29.)
(9.29.)
для параболы второго порядка:
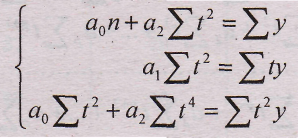 (9.30.)
(9.30.)
Решая системы (9.29) и (9.30), получим величины параметров соответствующих полиномов.
При сглаживании ряда динамики по показательной кривой (yt=a0a1t) для определения параметров применяется также метод наименьших квадратов, но только к логарифмам исходных данных. Так, для нахождения параметров показательной функции необходимо решить следующую систему уравнений:
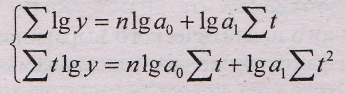 (9.31.)
(9.31.)
Если ∑t=0, то параметры уравнения lg а0 и lg a1 находим по формулам:
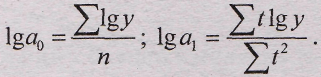
Пример. Необходимо определить основную тенденцию ряда динамики числа проданных квартир в N-ом регионе за 2000-2004 гг.
Таблица 9.7.
Таблица исходных и расчетных данных
| Годы | Число проданных квартир, тыс.ед. | t | t2 | yt | y¯t |
| А | |||||
| 2000 2001 2002 2003 2004 | 108 107 ПО HI 112 | -2 -1 +1 +2 | 4 1 0 1 4 | -216 -107 0 +111 +224 | 107,2 108,4 109,6 110,8 112,0 |
| Итого | +12 | 548,0 |
Первые две графы - ряд динамики, подвергаемый выравниванию, дополняются графой 2, в которой показана система отсчета времени «t». Причем эта система выбирается таким образом, чтобы Yt = 0. В качестве функции выравнивания выбрано уравнение прямой линии: y¯t = а0 + att, параметры данного уравнения находим по упрощенным формулам:
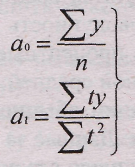
Затем в графах 3 и 4 проводим необходимые расчеты и находим: Уу = 548; Yyt = 12; yt2 = 10. Отсюда:
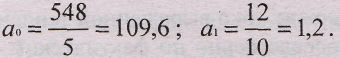
Уравнение прямой будет иметь вид: yt = 109,6 + 1,21.
На основе этого уравнения находятся выровненные годовые уровни путем подстановки в него соответствующих значений «t» (графа 5 таблицы 9.7).
Полученное уравнение показывает, что численность проданных квартир в регионе растет в среднем на 1,2 тысяч единиц в год. Таким образом, величина параметра ai в уравнении прямой показывает среднюю величину абсолютного прироста выровненного ряда динамики.
Сумма уровней эмпирического ряда (∑yi) полностью совпала с суммой расчетных значений выровненного ряда ( ∑y¯e ).
Результаты произведенного аналитического выравнивания ряда динамики проданных квартир за 2000-2004 гг. и фактические данные отражены на рисунке 9.2
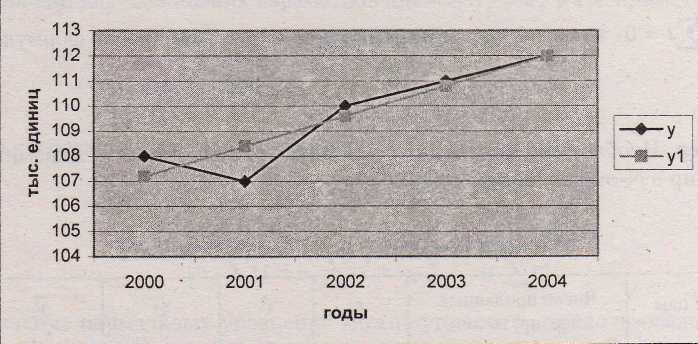
Рис. 9.2. Динамика численности проданных квартир в N-ом регионе за 2000,-2004 гг.
 2015-04-20
2015-04-20 455
455








