Движение м.т. под действием силы, зависящей только от координат. Одномерный случай

Такое движение осуществляется уже под действием силовых полей. Движение м.т. под действием силы f = f (r), зависящей только от координаты, происходит по–– закону:

d ² r / dt ² = f (r)

dv / dt = f (r)

Решить это уравнение проще, если воспользоваться законом сохранения энергии. Для этого заметим, что инеграл силы по координате x в одномерном случае всегда будет равен потенциальной энергии:

∫ f (r) = U (x)

Запишем уравнение закона сохранения энергии к нашему одномерному случаю:

½ v ² + U (x) = E

Это есть дифференциальное уравнение первого порядка, интегрирующееся путем разделения переменных. Имеем:

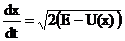
откуда:

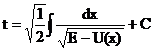
Роль двух произвольных постоянных в решении уравнения движения играют здесь полная энергия E и постоянная интегрирования C. Поскольку кинетическая энергия является величиной существенно положительной, то при движении полная энергия всегда больше потенциальной, и движение может происходить только в тех областях пространства, где U (x)≤ E.

Пусть, например, зависимость U (x) имеет вид, изображен­ный на рис. 9. Проведя на этом же графике горизонтальную прямую, соответствующую заданному значению полной энер­гии, мы сразу же выясним возможные области движения. Так в изображенном на рис. 9 случае движение может происходить лишь в области АВ или в области справа от С,

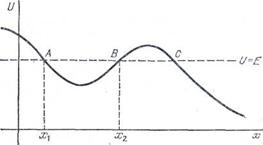
Рис. 9. Движение м.т. в потенциальном поле.

Точки, в которых потенциальная энергия равна полной

U (x) = E

определяют границы движения. Они являются точками оста­новки, поскольку в них скорость обращается в нуль. Если об­ласть движения ограничена двумя такими точками, то движе­ние происходит в ограниченной области пространства; оно яв­ляется, как говорят, финитным. Если же область движения не ограничена или ограничена лишь с одной стороны, — движение инфинитно, частица уходит на-бесконечность.

Одномерное финитное движение является колебательным - частица совершает периодически повторяющееся движение ме­жду двумя границами (на рис. 9 в потенциальной яме АВ ме­жду точками x ₁ и x ₂). При этом согласно общему свойству об­ратимости время движения от x ₁ до x ₂ равно времени обратного движения от x ₂ до x ₁. Поэтому период колебаний Т, т. е. время, за которое точка пройдет от x ₁ до x ₂ и обратно, равен удвоенному времени прохождения отрезка x ₁ x ₂ или:

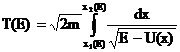
причем пределы x ₁ и x ₂ являются корнями уравнения (7.4.6), при данном значении Е. Эта формула определяет период дви­жения в зависимости от полной энергии частицы.

Движение м.т. под действием произвольных сил в 3-мерном пространстве не поддается общему решению, хотя в некоторых случаях это возможно. Такие примеры рассмотрены ниже.