Математическое описание и обработка гармонических сигналов осуществляются просто. В связи с этим периодический сигнал часто представляют в виде ряда Фурье, т. е. разлагают на гармонические составляющие. При этом гармонические составляющие могут быть описаны тремя равноценными способами. Для типовых периодических сигналов, таких как прямоугольные, пилообразные колебания и др., составлены таблицы соответствующих рядов Фурье.
7.5.1. Ряд Фурье как сумма синусоидальных и косинусоидальных колебаний. Ряд Фурье периодического сигнала по определению равен:
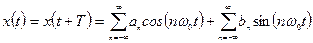 ,
,
где 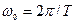 - круговая частота основной гармонической составляющей:
- круговая частота основной гармонической составляющей:
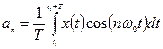 ;
;
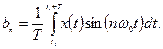
Смысл уравнения ряда Фурье при описании сигнала состоит в том, что вся информация о сигнале 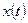 заключена в амплитудах
заключена в амплитудах 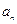 или
или 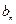 как функция дискретных частот
как функция дискретных частот 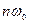 . Для периодических функций характерна дискретность амплитудных спектров
. Для периодических функций характерна дискретность амплитудных спектров 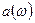 и
и 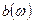 , т. е. они существуют только при дискретных величинах частоты
, т. е. они существуют только при дискретных величинах частоты 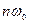 . Коэффициент ряда Фурье
. Коэффициент ряда Фурье 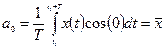 соответствует так называемой постоянной составляющей сигнала. Коэффициент
соответствует так называемой постоянной составляющей сигнала. Коэффициент 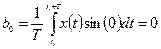 отсутствует в тех случаях, когда сигналы имеют вид последовательности прямоугольных импульсов.
отсутствует в тех случаях, когда сигналы имеют вид последовательности прямоугольных импульсов.
7.5.2. Ряд Фурье как сумма косинусоидальных колебаний с различным сдвигом фаз. На основании тригонометрической теоремы сложения ряд Фурье можно записать в следующей форме:
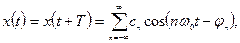
где 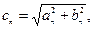
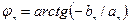
При этом описание сигнала 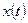 даётся в виде дискретного амплитудного спектра
даётся в виде дискретного амплитудного спектра 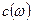 и дискретного фазового спектра
и дискретного фазового спектра 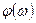 .
.
7.5.3. Ряд Фурье в комплексной форме. Наиболее просто ряд Фурье описывается с помощью комплексного коэффициента 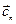 :
:
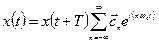 ;
;
где 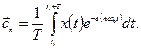
Используя уравнение Эйлера, можно показать, что
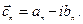
При этом векторная величина 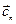 эквивалентна величинам
эквивалентна величинам 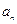 и
и 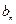 или
или 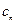 и
и 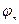 :
:
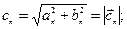
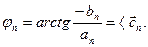
 2015-05-06
2015-05-06 228
228








