Из уравнений (1.8.1) и (1.8.7) следует, что
Р = nkТ (1.9.1)
Учитывая, что n = N/V и N/NА = m/μ = ν, получим
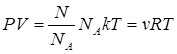 , (1.9.2)
, (1.9.2)
где введена постоянная R=kNA=8,31Дж/мольּК, которую называют универсальной газовой постоянной. Физический смысл её установим из уравнения (1.9.2):
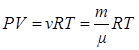 , (1.9.3)
, (1.9.3)
которое называют уравнением Менделеева-Клапейрона. Для этого запишем уравнение (1.9.3) для двух состояний изобарического процесса:
PV1 = νRT1
РV2=νRТ2
 |
Откуда находим
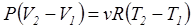 (1.9.4)
(1.9.4)
Обозначая V2 – V1= Δ V, T2 – T1= Δ T и учитывая, что работа при изобарическом процессе А =Р Δ V, из (1.9.4) найдём R.
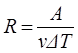 , (1.9.5)
, (1.9.5)
т.е. постоянная R численно равна работе при изобарическом нагревании на один кельвин (Δ Т = 1К) одного моля (ν = 1 моль) идеального газа. Так как k = R/NA, то постоянная Больцмана имеет тот же смысл, что и R, только рассчитанная на одну молекулу.
Из уравнения состояния идеального газа (1.9.3) можно получить известные из опыта газовые законы.
1. Полагая в уравнении (1.9.3) ν = const и Т = const, получаем
PV = const (1.9.6)
Отсюда вытекает формулировка закона Бойля-Мариотта (изотермический процесс): при неизменных массе и температуре идеального газа произведение его объёма на давление есть величина постоянная.
|
|
|
2. При изобарическом процессе P = const. Также ν = сonst. Поэтому из уравнения состояния (1.9.3) в этом случае
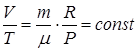 (1.9.7)
(1.9.7)
т.е. при неизменных массе и давлении идеального газа отношение объёма, занимаемого газом, к его температуре - величина постоянная. Это утверждение известно как закон Гей-Люссака.
3. Пусть процесс протекает при постоянном объёме V=const (попрежнему ν = сonst). Тогда из (1.9.3)
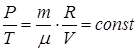 (1.9.8)
(1.9.8)
т.е. при неизменных массе и объёме идеального газа отношение давления газа к его температуре есть величина постоянная. Уравнение (1.9.8), называемое уравнением изохорического процесса, выражает известный закон Шарля.
4. Из уравнения (1.9.3), очевидно, также следует объединенныйзакон Мариотта – Гей – Люссака
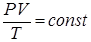 , (1.9.9)
, (1.9.9)
т.е произведение давления газа на его объем, деленные на абсолютную температуру, для данной массы газа есть величина постоянная.
5. Из уравнения (1.9.3) также следует закон, согласно которому при одинаковых давлениях и температурах в равных объёмах любого газа содержится одинаковое число молекул. Действительно, пусть имеются два одинаковых объёма двух различных газов при одинаковых давлениях и температурах. Для каждого из них можно написать уравнение состояния (1.9.2)
PV = N1kT, PV = N2kT,
где N1 и N2 - число молекул обоих газов. Из этих равенств непосредственно следует, что N1 = N2. Это и есть закон Авогадро. Из него, очевидно, следует и обратная формулировка: различные газы, но содержащие одинаковое число молекул, будут при одинаковых давлениях и температурах занимать одинаковые объёмы. Поэтому моль любого газа при данных давлении и температуре занимает одинаковый объём. В частности, при нормальных условиях (Т0 = 273,15 К, Ратм = 1,01ּ105 Па) моль любого газа занимает объём
|
|
|
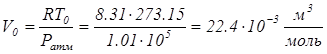
6. Следствием уравнения идеального газа является и закон Дальтона, утверждающий: давление смеси химически не реагирующих газов равно сумме парциальных давлений отдельных газов. Парциальным давлением называют давление, которое создал бы газ, если бы он находился один в объёме, занятом смесью.
Для доказательства закона Дальтона учтём, что в смеси нескольких газов общее количество молекул равно сумме количеств молекул отдельных газов
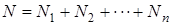 (1.9.10)
(1.9.10)
Подставим (1.9.10) в (1.9.3)
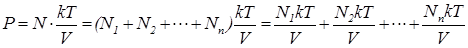 (1.9.11)
(1.9.11)
Каждое из слагаемых выражения (1.9.11) представляет собой парциальное давление. Поэтому
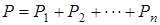 (1.9.12)
(1.9.12)
Что и требовалось доказать.
7. Наконец, следствием уравнения Менделеева – Клайперона является закон Амага΄: объем смеси химически нереагирующих идеальных газов равен сумме их парциальных объемов, т.е.
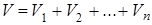 (1.9.13)
(1.9.13)
где парциальный объем
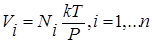 (1.9.14)
(1.9.14)
Как видно из выражения (1.9.14), парциальный объем Vi есть объем, который занимал бы i – ый газ, если бы все остальные газы были удалены, а давление Р и температура Т остались неизменными.
Для доказательства найдем из уравнения (1.9.2) идеального газа объем смеси
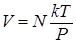 (1.9.10)
(1.9.10)
и подставим в него вместо N его выражение из (1.9.10). В результате получим
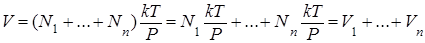 ,
,
что и доказывает справедливость закона Амага.
 2015-04-20
2015-04-20 680
680








