Построение пути на графе

В основе алгоритмов (табл. 1.1) построения кратчайшего пути m[ s, t ] между источником s и стоком t в ориентированном графе G = (X, U) лежат процедуры вычисления некоторых пометок l(x_i), приписываемых вершинам x_j Î X. Значения l(x_i), представляют собой верхние ограничения на длины путей m[ s, x_j ] от s до всех x_j, которые могут уменьшаться в процессе итерационных вычислений. Величина l(x_i) изменяется каждый раз при выполнении условия

l(x_i) + l (x_i, x_j) < l(x_j), (1.1)

где l (x_i, x_j) - длина дуги (x_i, x_j) Î U. Новое значение пометки определяется как

l(x_j) = l(x_i) + l (x_i, x_j).

Процесс прерывается, если ни одно из ограничений l(x_j) не может быть улучшено. Окончательное значение пометки l^*(x_j) показывает истинное значение длины кратчайшего пути m[ s, x_j ].

Таким образом, чтобы определить длину пути m[ s, t ], необходимо вычислить расстояния от s до всех вершин графа. При этом не существует алгоритма определения расстояния от источника s до стока t, который был бы более эффективным и не требовал вычислений длин путей m[ s, x_j ] до всех вершин x_j Î X \ s [6]. Методы вычисления значений l^*(x_j) для основных алгоритмов поиска кратчайшего пути на графе представлены в следующих разделах.

Построение пути на графе (т. е. определение последовательности вершин или дуг) по известным значениям l^*(x_j) может быть выполнено двумя способами. Пусть дуга (x_i, x_j) Î U лежит на кратчайшем пути m[ s, t ], т. е. (x_i, x_j) Î m[ s, t ]. Тогда для вершин x_i и x_j должно быть справедливым соотношение

l^*(x_j) = l^*(x_i) + l (x_i, x_j) (1.2)

Первый способ построения кратчайшего пути основан на систематической проверке условия (1.2). Здесь последовательность вершин графа, составляющих кратчайший путь m[ s, t ], определяется в обратном порядке, начиная от стока t. В частности, для пути

m[ s, t ] =(s, x ⁽¹⁾, x ⁽²⁾, …, x ^(k), t) (1.3)

можно найти вершину x ^(k) Î Г^-1(t), удовлетворяющую условию

l^*(x ^(k)) = l^*(t) - l (x ^(k), t).

Затем определяется вершина x ^{(k -1)}Î Г^-1(x ^(k)), для которой

l^*(x ^{(k -1)}) = l^*(x ^(k)) - l (x ^{(k -1)}, x ^(k)).

Процесс продолжается до тех пор, пока не будет достигнут источник s.

Второй способ построения пути предполагает неявное использование соотношения (1.2), когда уже при вычислении каждого значения l(x_j) указывается вершина, из которой ведет путь в x_j, уменьшающий величину l(x_j). В этом случае пометка любой вершины графа состоит из двух частей и имеет вид [l(x_j), m_j ], где m_j - вершина, из которой помечена x_j.

Значение m_j изменяется одновременно с l(x_j), т. е. если справедливо условие (1.1), то m_j = x_i. Окончательно, для пути m[ s, t ] вида (1.3) вершина x ^(k) определяется условием x ^(k) = m_t в соответствии с пометкой стока [l^*(t), m_t ]. На следующую вершину x ^{(k -1)} = m_k указывает пометка [l^*(x ^(k)), m_k ] и т.д.

У П Р А Ж Н Е Н И Я

1.9. Что показывают пометки, приписываемые вершинам графа в алгоритмах поиска кратчайшего пути?

1.10. Как используются значения пометок вершин для построения кратчайшего пути на графе?

1.11. Можно ли построить путь m[ s, t ], начиная от источника s?

1.12. Разработать подпрограмму построения кратчайшего пути в ориентированном графе по известным значениям пометок l^*(x_j). Длины дуг l (x_i, x_j) и структура графа G = (X, U) задается матрицей весов
D = 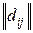_{n ´ n}, где d_ij = l (x_i, x_j) при (x_i, x_j) Î U и d_ij = ¥ при (x_i, x_j) Ï U.

1.13. Реализовать рекурсивный вариант подпрограммы построения пути m[ s, t ] по условиям предыдущего задания.

1.14. Построить кратчайшие пути m[ x_i, x_j ], 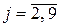, для графа, показанного на рис. 1.4. Значения l^*(x_j) пометок вершин x_j Î X приведены в упражнении 1.23.