2015-04-20
894
Пусть в замкнутой ограниченной пространственной области V, расположенной в декартовой прямоугольной системе координат Oxyz, определена непрерывная функция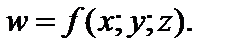 
Разобьем указанную область произвольным образом на элементарные области 
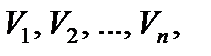объемы которых будем считать соответственно равными 
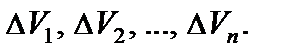Внутри каждой элементарной области выберем произвольную точку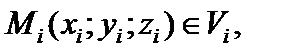 
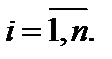
Диаметром области будем называть наибольшее из расстояний между любыми двумя точками границы области. Обозначим через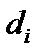 
диаметры элементарных областей 
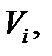а через 
– максимальный диаметр, т. е.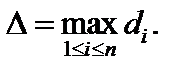 
Составим интегральную сумму функции f (x; y; z) в области V:
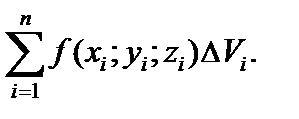
Устремим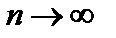 
так, чтобы 
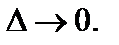Если существует предел интегральных сумм, который не зависит ни от способа разбиения области V на частичные области 
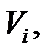ни от выбора точек 
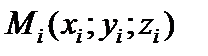внутри каждой из этих областей, то этот предел называется тройным интегралом от функции f (x; y; z) по области V:
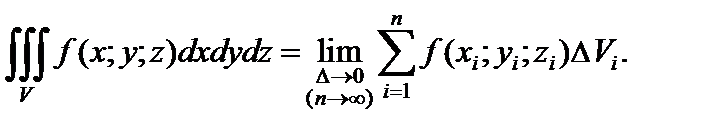
При этом говорят, что функция f (x; y; z) интегрируема в области V; x, y и z называют переменными интегрирования.
Достаточное условие интегрируемости функции: если определенная в некоторой ограниченной замкнутой области функция непрерывна, то она интегрируема в этой области.
|
|
|
Если функции f (x; y; z), f 1(x; y; z) и f 2(x; y; z) интегрируемы в области V, то имеют место следующие свойства:
1) линейность:
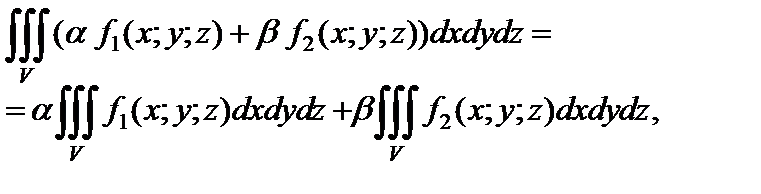
где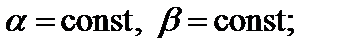 
2) аддитивность:
где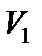 
и 
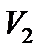– области, не имеющие общих внутренних точек;
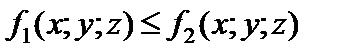
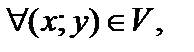3) если выполняется неравенство 
то
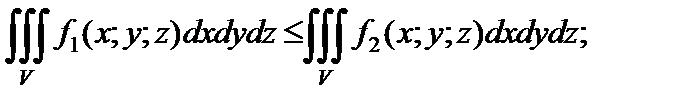
4) оценка модуля интеграла:
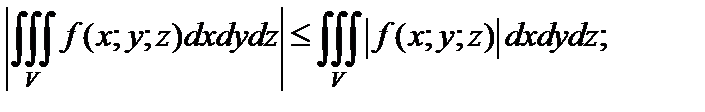
5) если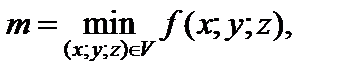 
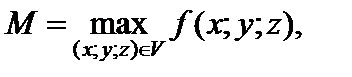то
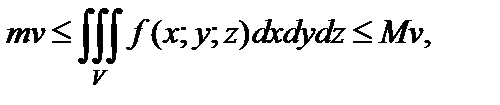
где v – объем области V.
