Астатические системы. Системы, у которых нет пропорциональной зависимости между выходным сигналом и ошибкой и у которых ошибка рассогласования в установившемся режиме равна нулю.
Жесткое управление. Управление, основанное на ретроспективной информации об объекте управления.
Координаты системы. Минимальная совокупность величин, полностью определяющих состояние системы.
Пространство состояний. Пространство, координаты которого являются координатами системы. При двух координатах – фазовая плоскость.
Программирование. Выходная величина системы меняется по заранее заданному алгоритму.
Слежение. Закон изменения выходной величины заранее неизвестен; он воспроизводит изменения задающего воздействия, следящего за изменениями некоторого внешнего фактора.
Стабилизация. Управление, при котором выходная величина поддерживается неизменной.
Управление по отклонению. Управляющее воздействие вырабатывается на основе информации об отклонении действительного состояния системы (выходной величины) от желаемого (задающего воздействия). В системе есть обратная связь, т.е. воздействие на систему результатов функционирования системы.
Статическая система. Система, у которой существует прямопропорциональная зависимость между выходным сигналом и ошибкой рассогласования и эта ошибка в установившемся режиме может быть очень небольшой, но не может быть равной нулю (системы управляются ошибкой).
Управление по возмущению. Управляющее воздействие формируется с учетом измеряемых возмущений (помех).
Устойчивость. Упрощенно, это динамическая система, обладающая ограниченной реакцией на ограниченный входной сигнал. Иначе – система устойчива, если собственные переходные процессы являются затухающими.
ГЛАВА 2. Основные динамические звенья систем автоматического управления. Их основные характеристики.
Динамическим звеном называют часть системы, которая описывается дифференциальным (или интегральным) уравнением. В общем случае порядок уравнения может быть произвольным, а звено сколь угодно сложным. Сложные звенья могут быть разложены на простейшие, элементарные звенья. К элементарным звеньям принято относить звенья, которые описываются дифференциальным уравнением не выше второго порядка. Это следующие звенья:
- пропорциональное (безынерционное) звено;
- интегрирующее звено;
- дифференцирующее звено;
- апериодическое звено;
- колебательное звено;
- звено с чистым запаздыванием.
Основные характеристики звеньев и систем делятся на три вида:
1. математическая характеристика (к ней относят передаточную функцию);
2. частотные характеристики (к ним относят амплитудно-фазовую характеристику, график которой называется годограф, амплитудно-частотную характеристику, фазо-частотную характеристику);
3. временные характеристики (переходная характеристика или переходная функция, весовая или импульсная переходная функция).
2.1 основные свойства Преобразования Лапласа, передаточная функция, ее нули и полюса.
1. Преобразование Лапласа. Преобразованием Лапласа называют преобразование функции 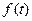 переменной
переменной 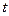 в функцию
в функцию 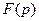 комплексной переменной
комплексной переменной 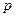 при помощи интеграла:
при помощи интеграла:
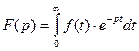 , (*)
, (*)
где функция 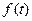 называется оригиналом, функция
называется оригиналом, функция 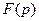 - изображением функции
- изображением функции 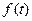 . Равенство (*) записывают также в виде:
. Равенство (*) записывают также в виде:
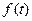
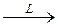
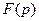 ,
, 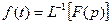 .
.
Преобразование Лапласа обладает следующими свойствами:
1. Линейность.
- Теорема суперпозиции. Изображение суммы конечного числа слагаемых есть сумма изображений этих слагаемых:
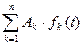
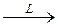
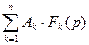 ,
, 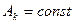
- Теорема линейности. Изображение произведения функции на постоянную величину равно произведению изображения функции на эту величину:
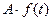
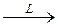
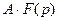 ,
, 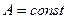 .
.
2. Теорема подобия (изменения масштаба):
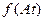
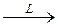
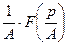 ,
, 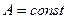 .
.
3. Теорема запаздывания. Если оригинал смещается вдоль оси 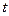 на постоянную t, то
на постоянную t, то
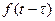
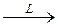
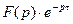 .
.
4. Теорема смещения:
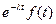
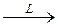
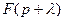 ,
, 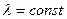 .
.
5. Дифференцирование при нулевых начальных условиях:
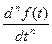
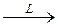
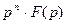 .
.
6. Дифференцирование при ненулевых начальных условиях:
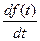
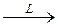
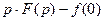 ,
,
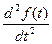
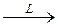
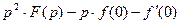 ,
,
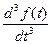
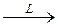
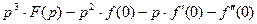 и т.д.
и т.д.
7. Интегрирование:
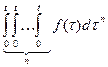
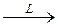
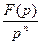 .
.
8. Предельные теоремы:
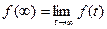 =
= 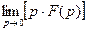 ,
,
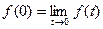 =
= 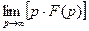 .
.
Предельные теоремы можно использовать, если известно, что 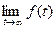 и
и 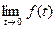 существуют.
существуют.
Таблица 1. Соответствия между оригиналом
и изображением наиболее распространенных функций.
| Название функции | Оригинал 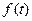
| Изображение |
| 1. Постоянная величина. |
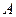 , ,
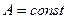
|
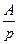
|
| 2. Степенная функция. |
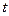
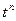
| 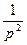
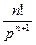
|
3. Экспонента,
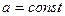
|
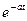
| 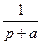
|
4. Смещенная экспонента, 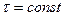
| 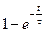
| 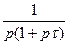
|
| 5. Синусоида. |
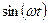
| 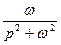
|
| 6. Косинусоида. |
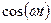
| 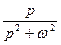
|
| 7. Затухающая синусоида. |
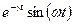
| 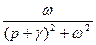
|
8. 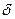 -функция. -функция.
| 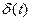
|
2. Передаточная функция. Рассмотрим некоторую систему:
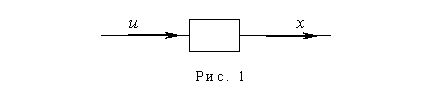
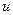 - входной сигнал,
- входной сигнал, 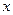 - выходной сигнал (координата системы).
- выходной сигнал (координата системы).
Пусть данная система описывается дифференциальным уравнением 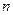 -го порядка:
-го порядка:
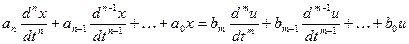 .
.
В реальных системах всегда справедливо следующее неравенство:
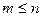 .
.
Дифференциальное уравнение, описывающее систему, записано во временном пространстве. Используя преобразование Лапласа, перейдем в пространство Лапласа, считая начальные условия нулевыми:
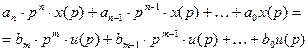
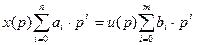
Передаточная функция этоотношение лапласовского изображения выходной величины к лапласовскому изображению входной величины (при нулевых начальных условиях). Согласно этому определению выражение для передаточной функции имеет следующий вид:
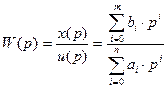 ,
,
т.е. передаточная функция равна отношению операторного полинома, стоящего при входной переменной, к операторному полиному, стоящему при выходной переменной.
Пример 1. Система описывается следующим дифференциальным уравнением:
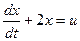 .
.
Необходимо найти передаточную функцию 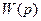 системы.
системы.
Перейдем в пространство Лапласа; для получения изображений воспользуемся таблицей соответствий:
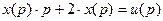
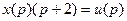
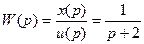 .
.
Пример 2. Задано следующее дифференциальное уравнение:
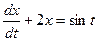 .
.
Необходимо найти передаточную функцию 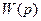 системы.
системы.
Перейдем в пространство Лапласа:
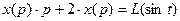
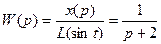 .
.
Нули передаточной функции - это корни уравнения:
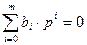 .
.
Полюса передаточной функции - это корни уравнения:
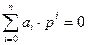 .
.
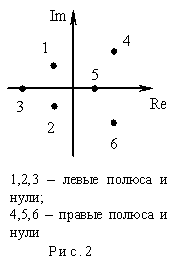
Нули и полюса делятся на левые и правые. Левые полюса и нули расположены в левой полуплоскости комплексной плоскости, а правые, соответственно, в правой полуплоскости (см. рис.2).
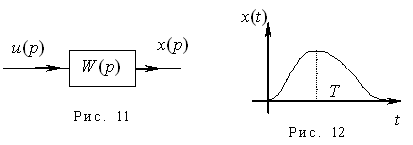
Ранее были рассмотрены односвязные системы, т.е. системы, имеющие один вход и один выход. Но существуют еще и многосвязные системы, имеющие большее число входов и выходов (рис.3).
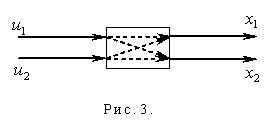
Входные сигналы 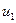 ,
, 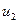 оказывают влияние на каждый из выходных сигналов
оказывают влияние на каждый из выходных сигналов 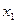 и
и 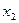 . Связь между входными и выходными сигналами:
. Связь между входными и выходными сигналами:
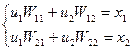 ,
,
в векторной форме:
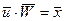 ,
,
где 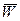 - передаточная функция многосвязной системы, она определяется как
- передаточная функция многосвязной системы, она определяется как
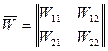 ,
, 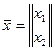 ,
, 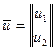 .
.
2.2 ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ.
1. Получение частотных характеристик, их виды. Пусть система имеет следующую передаточную функцию:
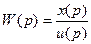 ,
,
где 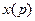 - лапласовское изображение выходного сигнала,
- лапласовское изображение выходного сигнала, 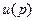 - лапласовское изображение входного сигнала. Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной
- лапласовское изображение входного сигнала. Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной 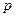 на
на 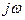 . Указанная замена равносильна переходу к преобразованию Фурье для дифференциальных уравнений при нулевых начальных условиях. Таким образом, получим следующее выражение:
. Указанная замена равносильна переходу к преобразованию Фурье для дифференциальных уравнений при нулевых начальных условиях. Таким образом, получим следующее выражение:
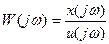 .
.
Перейдем к показательной форме представления комплексного числа:
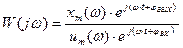 ,
,
где 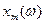 и
и 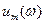 - амплитудные значения выходного и входного сигналов.
- амплитудные значения выходного и входного сигналов.
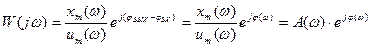
Функция 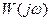 называется комплексным коэффициентом передачи (ККП) или амплитудно-фазовой характеристикой (АФХ). Она зависит от параметров элементов, составляющих автоматическую систему, и от частоты. Комплексный коэффициент передачи может быть представлен еще и в алгебраической форме, которая имеет следующий вид:
называется комплексным коэффициентом передачи (ККП) или амплитудно-фазовой характеристикой (АФХ). Она зависит от параметров элементов, составляющих автоматическую систему, и от частоты. Комплексный коэффициент передачи может быть представлен еще и в алгебраической форме, которая имеет следующий вид:
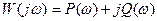 ,
,
где 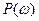 - вещественная частотная характеристика,
- вещественная частотная характеристика, 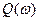 - мнимая частотная характеристика.
- мнимая частотная характеристика.
Кроме АФХ существуют и другие частотные характеристики. Функция 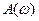 называется амплитудно-частотной характеристикой (АЧХ), он определяет зависимость амплитуды от частоты. Функция
называется амплитудно-частотной характеристикой (АЧХ), он определяет зависимость амплитуды от частоты. Функция 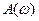 определяется следующим образом:
определяется следующим образом:
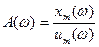 ,
,
или, используя алгебраическую форму представления АФХ,
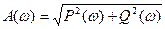 .
.
Функция 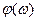 называется фазо-частотной характеристикой (ФЧХ), она определяет зависимость фазы от частоты.. Функция
называется фазо-частотной характеристикой (ФЧХ), она определяет зависимость фазы от частоты.. Функция 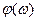 определяется следующим образом:
определяется следующим образом:
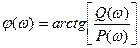 .
.
ФЧХ и АЧХ чаще всего строят в логарифмическом масштабе. Это позволяет сжимать область изображения, операции умножения и деления заменяются операциями сложения и вычитания. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) определяется следующим образом:
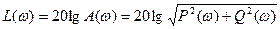 .
.
2. Амплитудно-фазовая характеристика. График амплитудно-фазовой характеристики называется годографом (рис. 4). Годограф – это линия, которую описывает на комплексной плоскости конец вектора комплексного коэффициента передачи при изменении частоты от нуля до бесконечности (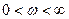 ). Теоретически частотные характеристики могут быть построены и для отрицательных частот, но это имеет чисто математический, а не физический смысл. Годограф применяется для исследования устойчивости систем.
). Теоретически частотные характеристики могут быть построены и для отрицательных частот, но это имеет чисто математический, а не физический смысл. Годограф применяется для исследования устойчивости систем.
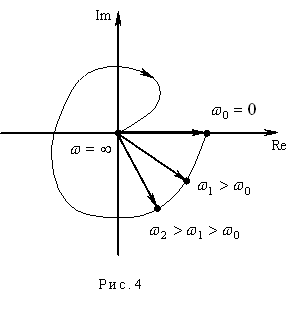
3. Построение асимптотических ЛАЧХ и ЛФЧХ. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) определяет изменение логарифма модуля частотной функции при изменении частоты. На графике логарифм модуля откладывают по оси ординат, а логарифм частоты – по оси абсцисс.
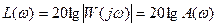
данное выражение определяет логарифм отношения амплитуды на выходе к амплитуде на входе и характеризует степень усиления системой входного сигнала, поэтому эту величину измеряют в единицах, принятых для усилительных устройств. Но логарифмическая единица бел считается очень крупной, поэтому величина 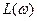 выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Децибел равен одной десятой части бела. Один децибел соответствует изменению амплитуды в
выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Децибел равен одной десятой части бела. Один децибел соответствует изменению амплитуды в 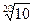 раз.
раз.
| Разы |
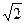
| 103 | 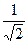
| 0,1 | |||
| Децибелы, db | -3 | -20 |
При построении логарифмических характеристик используют также следующие единицы: октава и декада.
Октавой называют отрезок оси 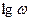 , заключенный между произвольным и удвоенным значением
, заключенный между произвольным и удвоенным значением 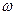 . Длина этого отрезка:
. Длина этого отрезка:
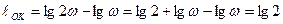 .
.
Декадой называется отрезок оси абсцисс, заключенный между произвольным значением 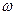 и его десятикратным значением
и его десятикратным значением 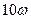 . Длина этого отрезка:
. Длина этого отрезка:
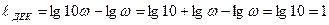
Для построения ЛАЧХ и ЛФЧХ часто используют асимптотическое, т.е. приближенное, построение. Наиболее часто применяемый способ это построение по Боде. Асимптотическая аппроксимация по Боде заключается в отбрасывании в сумме меньших из слагаемых.
Пример 1 (построение ЛАЧХ и ЛФЧХ по Боде): система описывается следующей передаточной функцией:
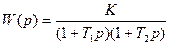 ,
,
где 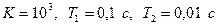 .
.
Перейдем к комплексному коэффициенту передачи:
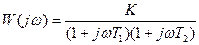 , (*)
, (*)
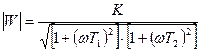 ,
,
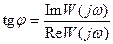 .
.
Найдем частоты сопряжения, т.е. те частоты где асимптотические ЛАЧХ и ЛФЧХ терпят излом:
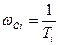
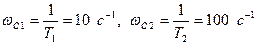 .
.
Запишем выражение (*) через сопряженные частоты:
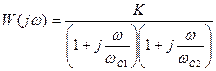 .
.
1) 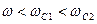 , т.е.
, т.е. 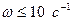 . Тогда ККП примет вид:
. Тогда ККП примет вид:
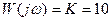
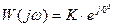 .
.
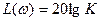
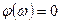
2) 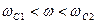 . Тогда ККП примет вид:
. Тогда ККП примет вид:
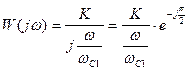 ,
,
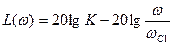 ,
,
приращение ЛАЧХ составляет 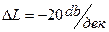 .
.
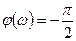 .
.
3) 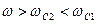 . Тогда ККП примет вид:
. Тогда ККП примет вид:
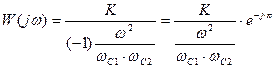 ,
,
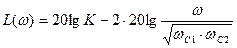 ,
,
приращение ЛАЧХ составляет 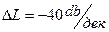 ,
,
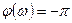 .
.
Асимптотические и точные характеристики довольно хорошо совпадают для ЛАЧХ и хуже для ЛФЧХ. Наибольшее расхождение для фазовых характеристик имеется в области сопряженных частот. Построенные характеристики изображены на рис. 5, где сплошной линией построены асимптотические характеристики, а точные – пунктиром с точкой.
Пример 2. Система описывается передаточной функцией:
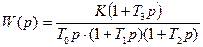 ,
,
где 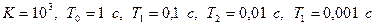 .
.
Перейдем к комплексному коэффициенту передачи:
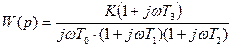 , (*)
, (*)
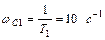 ,
, 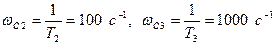
Запишем выражение (*) через сопряженные частоты:
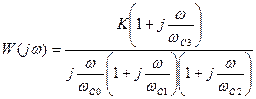 .
.
1) 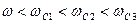 , т.е.
, т.е. 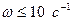 . Тогда ККП примет вид:
. Тогда ККП примет вид:
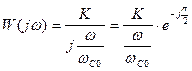 , где
, где 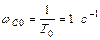
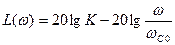 ,
,
приращение ЛАЧХ составляет 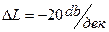 .
.
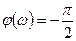 .
.
2) 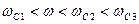 , т.е.
, т.е. 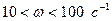 :
:
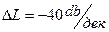 ,
, 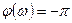 .
.
3) 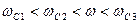 , т.е.
, т.е. 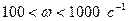 :
:
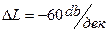 ,
, 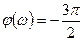 .
.
3) 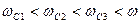 , т.е.
, т.е. 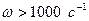 :
:
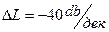 ,
, 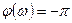 .
.
ЛАЧХ и ЛФЧХ для данной системы представлены на рис. 6. 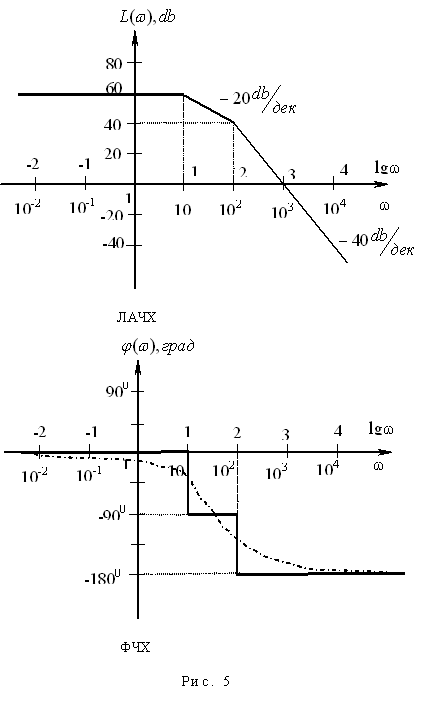
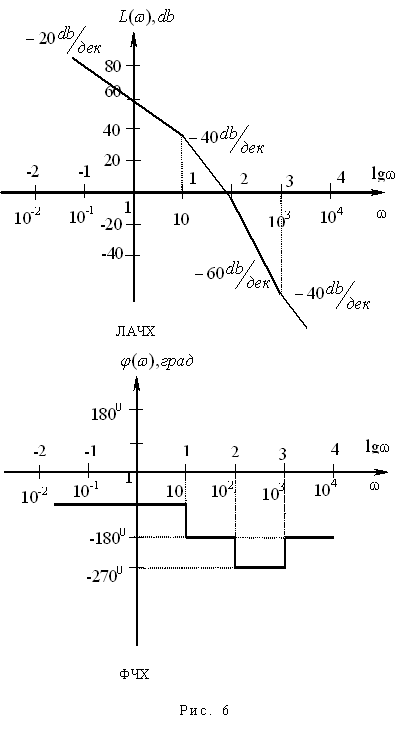
2.3 ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ.
Линейные системы обладают следующим «замечательным» свойством, если известна реакция системы (выходной сигнал) на некоторое входное воздействие, то можно рассчитать с помощью интеграла Дюамеля реакцию система на любой другой сигнал. Линейные системы полностью характеризуются реакциями на следующие стандартные входные сигналы:
1. единичная функция, реакция на этот сигнал носит название переходная функция.
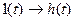
2. d-функция, реакция на этот входной сигнал носит название импульсная (или весовая) функция.
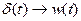
1. Переходная функция. Единичная функция – это функция следующего вида, (рис. 7):
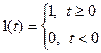 .
.
Рассмотрим некоторое звено с передаточной функцией 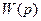 , сигналом на входе
, сигналом на входе 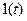 и сигналом на выходе
и сигналом на выходе 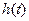 (рис.8):
(рис.8):
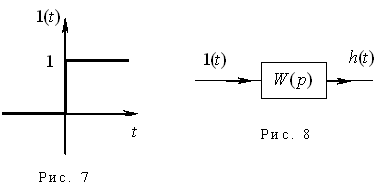
Перейдем в пространство Лапласа:
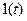
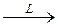
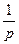
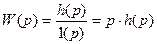
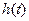
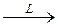
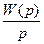 ;
; 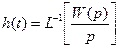
При определении переходной функции для проверки результатов полезно пользоваться предельными теоремами:
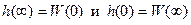 .
.
Пример 1. Рассмотрим некоторое звено, которое описывается следующей передаточной функцией:
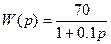 .
.
Необходимо найти переходную функцию:
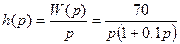 .
.
Найдем оригинал переходной функции, использую стандартную таблицу соответствий:
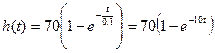 .
.
Проверка:
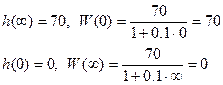 .
.
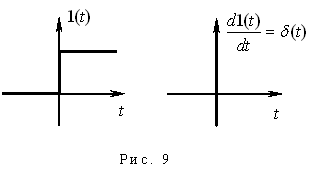
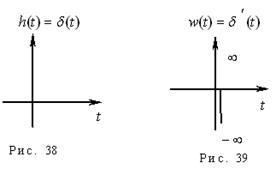
2. Импульсная (весовая) функция. d-функция, или функция Дирака, - это функция следующего вида, (рис. 9):
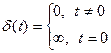 .
.
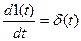 ,
,
последнее уравнение в пространстве Лапласа:
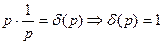 .
.
Рассмотрим некоторое звено с передаточной функцией 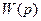 , сигналом на входе
, сигналом на входе 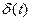 и сигналом на выходе
и сигналом на выходе 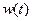 (рис.10):
(рис.10):
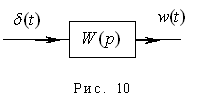
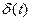
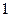
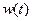
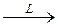
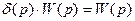
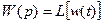
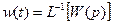 ,
,
т.е. импульсная (весовая) функция является оригиналом передаточной функции.
Пример 2. Условия такие же, как в примере 1. Необходимо найти весовую функцию:
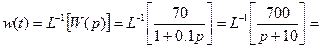
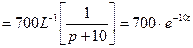
Пример 3 (применение интеграла Дюамеля):
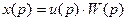
Перейдем во временное пространство:
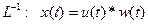 .
.
Знак 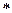 обозначает свертку функций.
обозначает свертку функций.
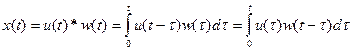 .
.
Пусть
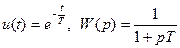 .
.
Необходимо найти 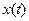 . Для этого сначала найдем весовую функцию:
. Для этого сначала найдем весовую функцию:
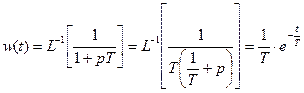 ,
,
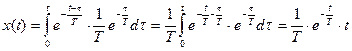 .
.
2.4 ПРОПОРЦИОНАЛЬНОЕ (БЕЗЫНЕРЦИОННОЕ) ЗВЕНО.
1. Передаточная функция. Частотные и временные характеристики звена. Уравнение динамики идеального звена имеет вид:
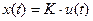
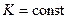 - коэффициент усиления (или передачи), который является постоянным для линейного звена и переменным для нелинейного звена.
- коэффициент усиления (или передачи), который является постоянным для линейного звена и переменным для нелинейного звена.
Перейдем к операторной форме записи уравнения:
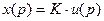 .
.
Передаточная функция пропорционального звена
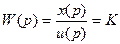 .
.
Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной 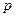 на
на 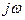 :
:
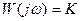 .
.
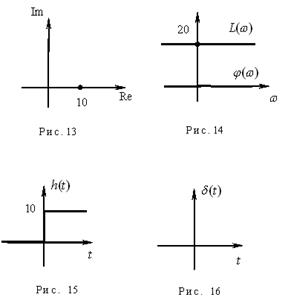
Пусть 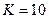 , тогда
, тогда 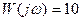 , для данного случая построим годограф (рис. 13).
, для данного случая построим годограф (рис. 13).
Найдем ЛАЧХ:
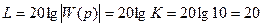 .
.
Перейдем к показательной форме представления комплексного числа:
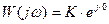 ,
,
тогда ФЧХ:
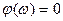 .
.
Графики ЛАЧХ и ФЧХ представлены на рис.14.
Получим переходную характеристику (рис. 15):
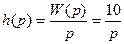 .
.
Весовая функция (рис. 16):
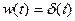 .
.
2. Примеры пропорционального звена. Его реализация на операционном усилителе.
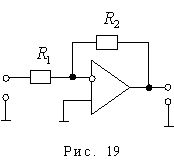
- Усилитель (рис. 17): для того чтобы на практике иметь идеальное пропорциональной (инерционное) звено, необходимо чтобы частота входного сигнала была 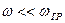 .
.
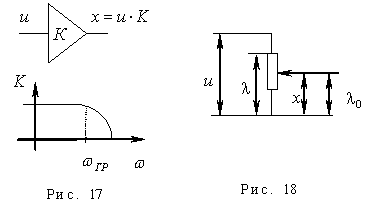
- Потенциометр (рис. 18): коэффициент передачи определяется следующим образом:
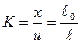 .
.
Жесткий механический рычаг: коэффициент передачи определяется как отношение плеч рычага.
- Механический редуктор и т.д.
Схема реализации пропорционального звена на операционных усилителях имеет следующий вид (рис. 19). Передаточная функция определяется следующим образом:
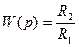 .
.
Статический коэффициент передачи:
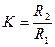 .
.
2.5 интегрирующее звено (интегратор).
Интегратор – это звено, в котором входному сигналу пропорциональна производная выходной величины.
1. Передаточная функция. Частотные и временные характеристики звена. Уравнение динамики интегрирующего звена имеет вид:
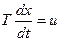 ,
,
или
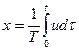 .
.
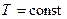 - коэффициент пропорциональности или постоянная времени.
- коэффициент пропорциональности или постоянная времени.
Перейдем к операторной форме записи уравнения, для этого применим преобразование Лапласа при нулевых начальных условиях:
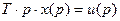 .
.
Передаточная функция интегрирующего звена
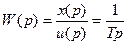 .
.
Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной 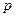 на
на 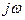 :
:
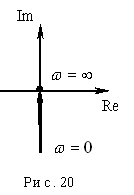
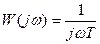 .
.
Построим годограф (рис. 20), годограф для данного звена совпадает с мнимой отрицательной полуосью.
Перейдем к показательной форме представления комплексного числа:
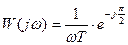 .
.
Тогда ЛАЧХ примет вид:
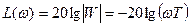 ,
,
если 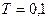 , то
, то
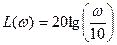 .
.
ЛАЧХ интегрирующего звена является прямой линией, проходящей с наклоном 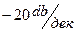 через точку на оси абсцисс, соответствующей значению
через точку на оси абсцисс, соответствующей значению 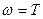 -1.
-1.
Определим ФЧХ:
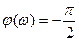 .
.
Характеристика показывает, что фаза не зависит от частоты (является постоянной).
Графики ЛАЧХ и ФЧХ представлены на рис.21.
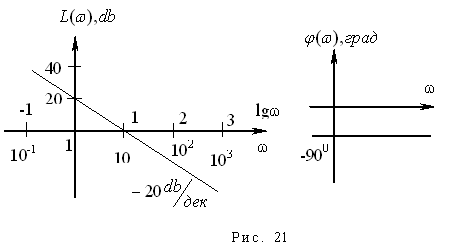
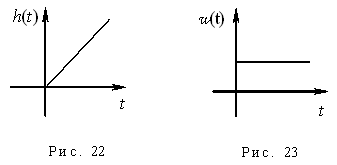
Получим переходную характеристику (рис. 22):
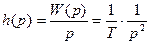
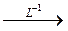
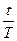
Весовая функция (рис. 23):
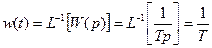 .
.
2. Примеры интегрирующего звена. Его реализация на операционном усилителе.
- Конденсатор (рис. 24):
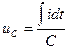 .
.
- Выходной вал двигателя (рис. 25):
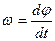 ,
,
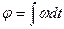 ,
,
где 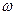 - угловая скорость вращения вала двигателя,
- угловая скорость вращения вала двигателя, 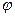 - угол поворота вала двигателя.
- угол поворота вала двигателя.
- Емкость с жидкостью (рис. 26).
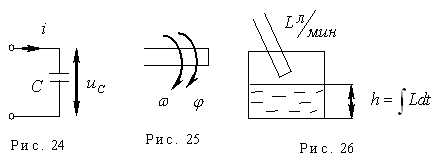
- Поршневой гидравлический сервомотор при пренебрежении массой и силой трения.
- Центробежный маятник при специальном подборе характеристик центробежной силы и пружины и т.д.
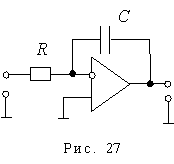 Схема реализации интегрирующего звена на операционных усилителях имеет следующий вид (рис.27). Передаточная функция при идеальном операционном усилителе:
Схема реализации интегрирующего звена на операционных усилителях имеет следующий вид (рис.27). Передаточная функция при идеальном операционном усилителе:
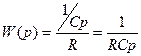 .
.
Постоянная времени интегратора:
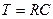 .
.
2.6 апериодическое звено первого порядка.
Это звено называют также инерционным.
1. Передаточная функция. Частотные и временные характеристики звена. Уравнение динамики апериодического звена имеет вид:
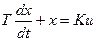 ,
,
где 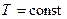 - постоянная времени, обусловленная наличием массы, момента инерции, индуктивности, емкости и т.д.,
- постоянная времени, обусловленная наличием массы, момента инерции, индуктивности, емкости и т.д., 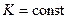 - коэффициент усиления (или передачи).
- коэффициент усиления (или передачи).
Возможно два частных случая:
1) 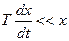 , т.е. величина
, т.е. величина 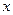 изменяется с малой скоростью, тогда уравнение может быть записана следующим образом:
изменяется с малой скоростью, тогда уравнение может быть записана следующим образом: 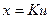 .
.
2) 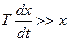 , уравнение может быть записано
, уравнение может быть записано
следующим образом: 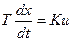 .
.
Перейдем к операторной форме записи уравнения, для этого применим преобразование Лапласа при нулевых начальных условиях:
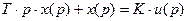 ,
,
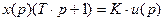
Передаточная функция апериодического звена
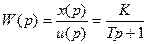 .
.
Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной 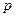 на
на 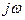 :
:
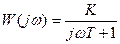 (*)
(*)
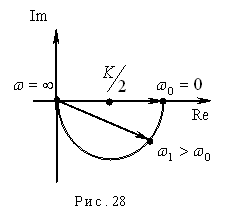
Построим годограф (рис. 28). Годограф для данного звена представляет собой полуокружность с центром на вещественной оси, находящимся на расстоянии 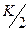 от начала координат.
от начала координат.
Выражение (*) может быть записано в следующей форме:
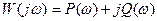 ,
,
где
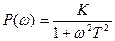 ,
,
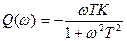
Перейдем к показательной форме представления комплексного числа:
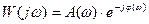 ,
,
где
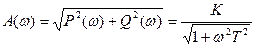 ,
,
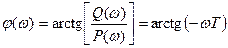 .
.
Тогда ЛАЧХ примет следующий вид:
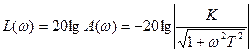 .
.
Асимптотические графики ЛАЧХ и ФЧХ данного звена представлены на рис.29.
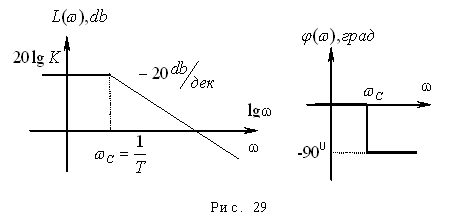
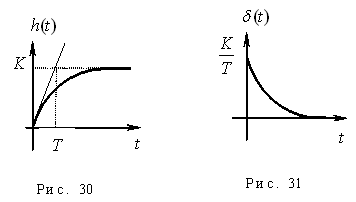
Получим переходную характеристику (рис. 30):
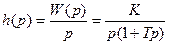 ,
,
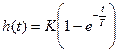 .
.
Весовая функция (рис. 31):
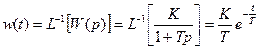 .
.
2. Примеры апериодического звена. Его реализация на операционном усилителе.
- Пассивные четырехполюсники, состоящие из сопротивления и индуктивности или сопротивления и емкости.
- Термопара.
- Магнитный усилитель (при определенных допущениях).
 - Генераторы постоянного и переменного тока.
- Генераторы постоянного и переменного тока.
- Электрические двигатели (если вход – ток якоря, а выход угловая скорость).
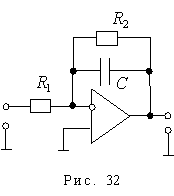
Схема реализации апериодического звена на операционных усилителях имеет следующий вид (рис. 32). Передаточная функция определяется следующим образом:
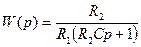 .
.
Постоянная времени:
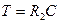 .
.
Коэффициент усиления:
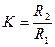 .
.
2.7 колебательное звено.
Это звено называют также инерционным звеном второго порядка.
Уравнение динамики инерционного звена второго порядка имеет вид:
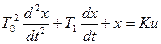 ,
,
где 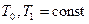 - постоянные времени,
- постоянные времени, 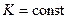 - коэффициент усиления (или передачи).
- коэффициент усиления (или передачи).
В зависимости от вида корней характеристического уравнения инерционное звено второго порядка может иметь различные переходные характеристики. Это позволяет установить две разновидности звена – апериодическое и колебательное. В случае вещественных корней получаем апериодическое звено второго порядка, которое эквивалентно последовательному соединению двух апериодических звеньев первого порядка.
Если корни характеристического уравнения комплексные, то инерционное звено второго порядка называется колебательным. В данном случае разложение звена на простейшие возможно, но получается довольно сложным и малополезным для практических целей. Поэтому колебательное звено относится к элементарным звеньям.
1. Передаточная функция. Частотные и временные характеристики звена. Уравнение динамики колебательного звена имеет вид:
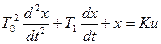 .
.
Перейдем к операторной форме записи уравнения, для этого применим преобразование Лапласа при нулевых начальных условиях:
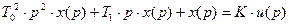 ,
,
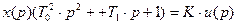 .
.
Передаточная функция колебательного звена
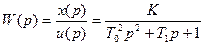 .
.
Характеристическое уравнение для данного звена запишется:
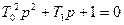 ,
,
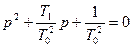 ,
,
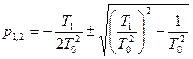 .
.
Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной 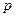 на
на 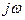 :
:
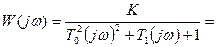
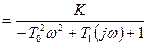 .
.
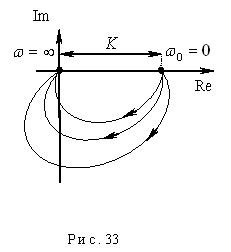
Годограф изображен на рис. 33. Амплитудно-фазовые характеристики приведены для разных значений 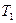 и
и 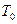 .
.
Графики ЛАЧХ и ФЧХ данного звена представлены на рис. 34.
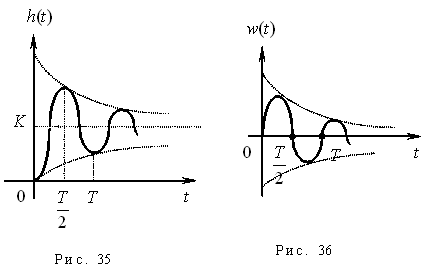
Переходная характеристика (рис. 35) для колебательного звена при комплексных корнях р1 и р2:
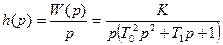 ,
,
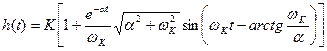 ,
,
где
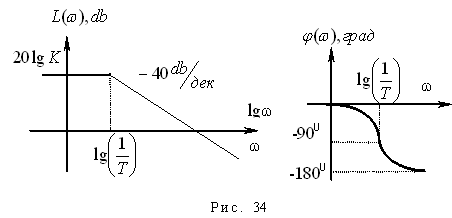
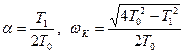 .
.
Весовая функция определяется как (рис. 36):
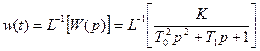 .
.
Пусть
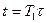 ,
,
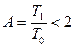 ,
,
тогда
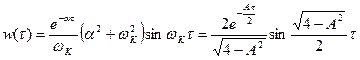 .
.
2. Примеры колебательного звена.
- Центробежный маятник.
- Контур, содержащий 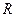 ,
, 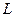 и
и 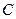 .
.
- Электромагнитный усилитель поперечного поля.
- Электродвигатель постоянного тока (если входом является напряжения якорной цепи, а выходом – скорость вращения при учете постоянной времени якоря и электромеханической постоянной времени).
2.8 дифференцирующее звено.
Дифференцирующие звенья реагируют на скорость изменения входного воздействия и могут быть описаны дифференциальными уравнениями, содержащими в правой части производную от входной переменной. Левая часть уравнения может иметь любой собственный оператор подобно рассмотренным выше звеньям. Рассмотрим наиболее общие случаи уравнений дифференцирующих звеньев:
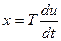 , (*)
, (*)
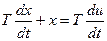 , (**)
, (**)
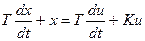 , (***)
, (***)
где 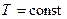 - постоянная времени,
- постоянная времени, 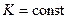 - коэффициент усиления (или передачи).
- коэффициент усиления (или передачи).
Уравнение (*) соответствует идеальному (безынерционному) дифференцирующему звену; (**) - реальному (инерционному) дифференцирующему звену без статизма;(***) - реальному 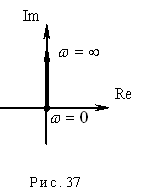 (инерционному) дифференцирующему звену со статизмом (или пропорционально-дифференцирующему звену). Рассмотрим идеальное дифференцирующее звено.
(инерционному) дифференцирующему звену со статизмом (или пропорционально-дифференцирующему звену). Рассмотрим идеальное дифференцирующее звено.
1. Передаточная функция. Частотные и временные характеристики звена. Уравнение динамики дифференцирующего звена имеет вид:
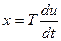 .
.
Перейдем к операторной форме записи уравнения, для этого применим преобразование Лапласа при нулевых начальных условиях:
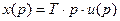 .
.
Передаточная функция идеального звена
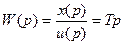 .
.
Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной 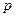 на
на 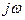 :
:
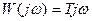 .
.
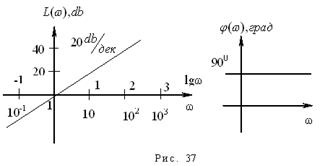
Построим годограф (рис. 37), годограф для данного звена совпадает с мнимой положительной полуосью.
Перейдем к показательной форме представления комплексного числа:
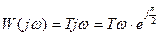 .
.
Тогда ЛАЧХ примет вид:
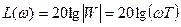 ,
,
если 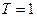 , то
, то
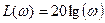 .
.
ЛАЧХ дифференцирующего звена является прямой линией, проходящей с наклоном 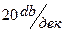 проходящую через точку на оси абсцисс, соответствующей значению
проходящую через точку на оси абсцисс, соответствующей значению 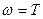 , если
, если 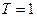 , прямая проходит через начало координат.
, прямая проходит через начало координат.
Определим ФЧХ:
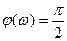 .
.
Фазо-частотная характеристика для дифференцирующего звена имеет вид прямой линии, параллельно оси абсцисс. Графики ЛАЧХ и ФЧХ представлены на рис. 37.
Получим переходную характеристику (рис. 38):
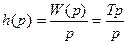 ,
,
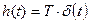 .
.
Весовая функция (рис. 39):
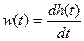 .
.
2. Примеры дифференцирующего звена. Его реализация на операционном усилителе.
- Электрические цепи, содержащие 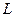 или
или 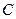 .
.
- Демпфер с пружиной.
- Тахогенератор, предназначенный для дифференцирования угла поворота вала электрической машины. Выходное напряжение тахогенератора определяется как:
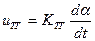 ,
,
где 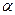 - угол поворота вала машины.
- угол поворота вала машины.
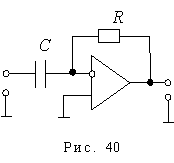
Схема реализации дифференцирующего звена на операционных усилителях имеет следующий вид (рис.40). Передаточная функция определяется следующим образом:
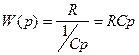 .
.
Постоянная времени:
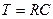 .
.
2.9 звено с чистым (транспортным) запаздыванием.
 Наиболее распространенным в практике автоматических систем является транспортное звено, обусловленное пространственным перемещением элементов, передающих информацию.
Наиболее распространенным в практике автоматических систем является транспортное звено, обусловленное пространственным перемещением элементов, передающих информацию.
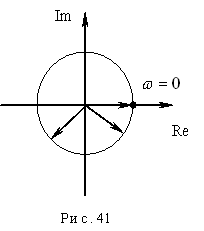
1. Передаточная функция. Частотные и временные характеристики звена. Уравнение динамики звена с запаздыванием имеет вид:
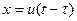 .
.
Перейдем к операторной форме записи уравнения, для этого применим преобразование Лапласа при нулевых начальных условиях:
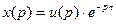 .
.
Передаточная функция звена с запаздыванием
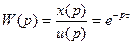 .
.
Частотные характеристики получаются путем замены в выражении передаточной функции комплексной переменной 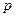 на
на 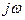 :
:
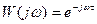 .
.
Годограф для данного звена является окружностью единичного радиуса, с центром в начале координат (рис. 41).
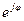 - вектор поворота, где
- вектор поворота, где 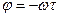 - угол поворота.
- угол поворота.
Тогда ЛАЧХ примет вид:
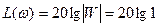 ,
,
т.е. ЛАЧХ для данного звена совпадает с осью абсцисс.
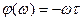 ,
,
фаза нарастает неограниченно с увеличением частоты.
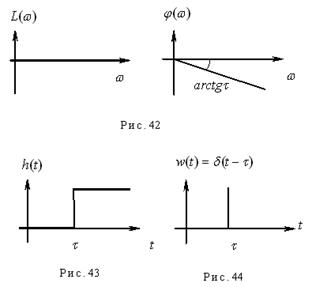
Графики ЛАЧХ и ФЧХ представлены на рис. 42.
Графики переходной характеристики и весовой функции представлены на рис. 43 и рис. 44.
2. Примеры звена с транспортным запаздыванием.
- Длинные трубопроводы и линии электропередач.
- Запись и считывание информации с помощью лентопротяжного механизма 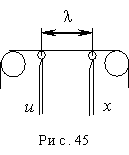 (рис. 45):
(рис. 45):
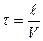 ,
,
где 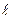 - длина ленты,
- длина ленты, 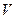 - скорость ленты.
- скорость ленты.
Ключевые термины и понятия.
Амплитудно-частотная характеристика. Зависимость модуля комплексного коэффициента передачи 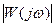 от частоты, обычно в логарифмическом масштабе.
от частоты, обычно в логарифмическом масштабе.
Годограф системы. Линия, которую описывает на комплексной плоскости конец вектора 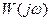 при изменении частоты от нуля до бесконечности.
при изменении частоты от нуля до бесконечности.
Импульсная переходная функция (весовая функция). Временная функция выходного сигнала при входном воздействии в виде дельта функции 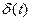 .
.
Комплексный коэффициент передачи (ККП). Передаточная функция в частотной области 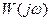 , возникающая при замене
, возникающая при замене 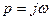 .
.
Переходная функция. Временная функция выходного сигнала при входном воздействии в виде единичной функции 1(t).
Передаточная функция. Отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.
Преобразование Лапласа. Интегральное преобразование функции времени f(t) в функцию комплексной переменной F(p).
Фазо – частотная характеристика. Зависимость аргумента ККП 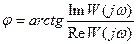 от частоты, обычно в полулогарифмическом масштабе.
от частоты, обычно в полулогарифмическом масштабе.
Характеристическое уравнение. Уравнение, получающееся приравниванием нулю знаменателя передаточной функции.
Элементарное звено. Звено, которое описывается дифференциальным уравнением не выше второго порядка.
 2015-04-30
2015-04-30 1093
1093








