Установившаяся (статическая) ошибка. Ошибка, остающаяся после полного затухания переходного процесса

ГЛАВА 4. Устойчивость линейных систем.

Самое первое требование, предъявляемое к системе, состоит в том, чтобы она была способна выполнять свои функции устойчиво. «Термин «устойчивость» настолько выразителен, что он сам за себя говорит» [5]. Но для математического анализа устойчивости требуется ее количественная характеристика.

Рассмотрим вначале понятия устойчивости равновесия и устойчивого движения.

Для исследования устойчивости равновесия предполагают, что система под действием внешнего толчка отклонилась от положения равновесия, и изучают те силы, которые возникают в результате этого отклонения. Если они в силу свойств системы стремятся вернуть систему в положение равновесия при любом направлении отклонения, равновесие устойчиво; если они стремятся увеличить отклонение, равновесие неустойчиво.

В случае движения системы заданное движение можно назвать невозмущенным движением. Приложение внешних сил к рассматриваемой системе вызовет отклонение действительного движения от заданного. Это движение будет возмущенным. Заданное невозмущенное движение называется устойчивым, если в результате приложения внешних сил, которые затем снимаются, возмущенное движение по истечении некоторого времени войдет в заданную область.

Теперь, основываясь на этих понятиях, рассмотрим устойчивость систем автоматического управления.

4.1 МАТЕМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ. РАСПОЛОЖЕНИЕ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ В УСТОЙЧИВОЙ СИСТЕМЕ.

Пусть имеется некоторая линейная система:

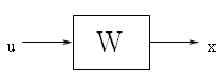
Эта линейная система описывается следующим дифференциальным уравнением:

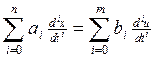(1)

Решение этого дифференциального уравнения представляется в виде суммы:

х = х_СВ + х_ВЫН (2)

Здесь х_СВ представляет собственные переходные процессы и является общим решением однородного дифференциального уравнения, х_ВЫН представляет процессы, возникающие вследствие внешнего воздействия, и является частным решением неоднородного дифференциального уравнения.

Система называется устойчивой, если собственные переходные процессы являются затухающими. Математически это можно записать:

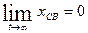(3)

Найдем эту составляющую. Для этого необходимо решить уравнение (1) без правой части.

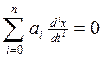(4)

Использовав преобразование по Лапласу, приходим к уравнению:

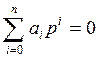(5)

Полученное алгебраическое уравнение называется характеристическим. Корни его p₁ , p₂ ,…, p_n б удут определять характер переходного процесса в системе.

Решение уравнения (4) представляется в виде:

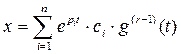, (6)

где r- кратность корня.

Рассмотрим различные положения корней характеристического уравнения (5) и влияние этого положения на устойчивость системы.

Корни могут быть левые (p ₁ , p ₂ , p ₃ ), правые (p ₄ , p ₅ , p ₆ ), нейтральные (p ₇ , p ₈ , p ₉ ).

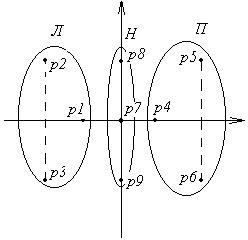
p _i =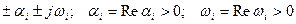

1) Левые корни

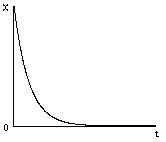а) p₁ = - 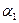, r =1

Из (6) получим:

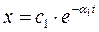
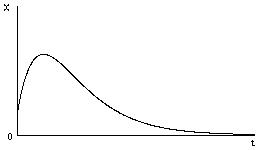
б) p₁ = - 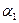, r =2

Из (6) получим:

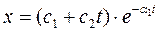
в) p_2,3 = - 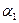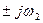, r =1

Из (6) получим:

=

=

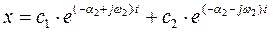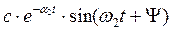
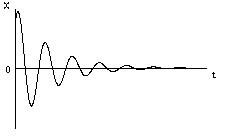
г) p_2,3 = - 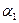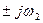, r =2

Из (6) получим:

=

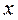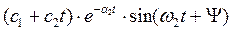
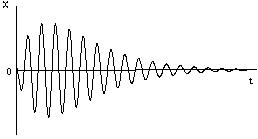
Вывод: левым корням соответствуют затухающие переходные процессы.

1) Правые корни.

а) p₄ = 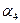, r =1

Из (6) получим:

=

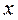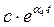
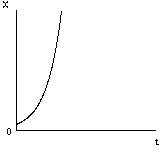
б) p_5,6 = 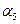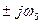, r =1

Из (6) получим:

=

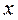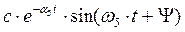
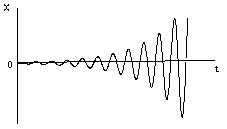
2) Нейтральные корни

а) p_8,9 = 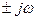, r =1

Из (6) получим:

=

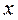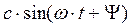
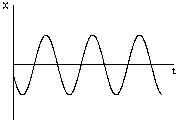
б) p ₇=0, х = c = const

Наличие нулевого корня показывает, что система устойчива не по отношению к 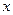, а по отношению к производной от .

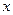Вывод: звено или система устойчива, если все корни характеристического уравнения левые. Если хотя бы один корень окажется справа от мнимой оси, то система будет неустойчивой. Таким образом, мнимая ось представляет собой граничную линию в плоскости корней, за которую не должны переходить корни характеристического уравнения. Вся левая плоскость при этом представляет собой область устойчивости.

Превращение устойчивой системы в неустойчивую произойдет в том случае, если хотя бы один вещественный или пара комплексных корней перейдет из левой полуплоскости в правую. Границей перехода будет так называемая граница устойчивости системы. Система будет находиться на границе устойчивости при наличии:

1) нулевого корня;

2) пары чисто мнимых корней;

Во всех случаях предполагается, что все остальные корни имеют отрицательные вещественные части.

4.2 алгебраические критерии устойчивости.

Для определения устойчивости системы нужно знать только расположение корней ее характеристического уравнения.

Существует ряд критериев, позволяющих определить устойчивость системы без решения соответствующего дифференциального уравнения. Все критерии устойчивости делятся на две группы: алгебраические критерии устойчивости и частотные критерии устойчивости.

Алгебраические критерии устойчивости позволяют определить устойчивость системы по коэффициентам соответствующего характеристического уравнения.

4.2.1 НЕОБХОДИМЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ.

Рассмотрим теорему Стодолы, определяющую необходимые условия устойчивости:

Если система устойчива (все корни левые), то все коэффициенты соответствующего характеристического уравнения положительны.

Характеристическое уравнение линейной системы n-го порядка в общем виде:

a _n p ⁿ + a _n-1 p ^n-1 +…+a₁ p + a₀ = 0 (1)

Если p₁ , p₂ ,…, p_n – корни характеристического уравнения, то это уравнение можно записать:

a_n (p – p₁)(p – p₂)…(p – p_n) = 0 (2)

Система устойчива, если все корни левые. Эти корни могут быть либо действительными, либо комплексно-сопряженными.

Проверим справедливость теоремы.

Для каждого левого действительного корня характеристического уравнения p₁ = - 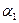, p₂ = 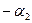выражение в скобках уравнения 2 будет положительным, а при преобразовании к виду 1 все коэффициенты будут положительны:

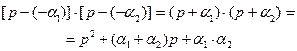
Т.е. можно отметить справедливость того, что коэффициенты характеристического уравнения действительно будут положительными.

Рассмотрим теперь пару комплексно-сопряженных корней характеристического уравнения p_1,2 = -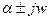

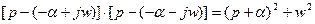
Отсюда тоже видно, что коэффициенты характеристического уравнения будут положительными.

Таким образом, установлена справедливость теоремы Стодолы.

Кроме того, нужно отметить, что положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости для систем первого и второго порядка.

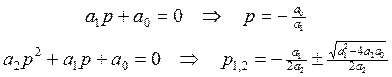
4.2.2 критерии УСТОЙЧИВОСТИ гурвица.

Большое распространение получил алгебраический критерий устойчивости, сформулированный в 1895 году математиком А.Гурвицем. Этот критерий был найден Гурвицем по просьбе словацкого профессора Стодолы, занимавшегося исследованием процесса регулирования турбин.

Пусть имеем линейную систему четвертого порядка. Ее характеристическое уравнение будет иметь вид:

a₄ p⁴ + a₃ p³ + a₂ p² + a₁ p + a₀ = 0

Составим матрицу 4 4, по диагонали которой располагаются коэффициенты характеристического уравнения. Строчки матрицы заполняются в соответствии со старшинством коэффициентов.

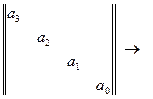
Диагональные миноры, составленные по главной диагонали матрицы Гурвица:

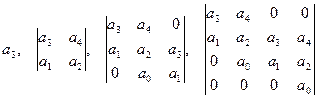
Для устойчивости системы необходимо и достаточно, чтобы все диагональные миноры в матрице Гурвица были положительны.

Рассмотрим характеристическое уравнение системы третьего порядка:

a₃ p³ + a₂ p² + a₁ p + a₀ = 0

Матрица Гурвица:

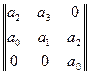
Диагональные миноры:

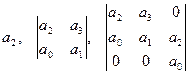
Первый минор a₂ > 0;

второй минор a₂ a₁ – a₀ a₃ > 0;

третий минор a₂ a₁ a₀ – a₀² a₃ > 0 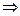a₂ a₁ – a₀ a₃ > 0 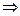a₂ a₁ > a₀ a₃.

Получаем, что для устойчивости линейной системы третьего порядка необходимо и достаточно, чтобы произведение внутренних коэффициентов характеристического уравнения было больше произведения наружных коэффициентов.

Уже для уравнения пятой степени условия устойчивости по критерию Гурвица получаются достаточно громоздкими. Поэтому использование этого критерия практически ограничивается уравнениями четвертого порядка.

Существенным недостатком критерия Гурвица является также то, что для уравнений высоких порядков в лучшем случае можно получить ответ о том, устойчива или неустойчива система автоматического регулирования. При этом в случае неустойчивой системы критерий не дает четкого ответа на то, каким образом нужно изменить параметры системы, чтобы сделать ее устойчивой. Это обстоятельство привело к поискам других критериев, которые были бы более удобными в инженерной практике.

Пример. В качестве примера рассмотрим следящую систему отработки угла.

Здесь W_ип – передаточная функция измерительного преобразователя:

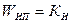, (1)

W_у – передаточная функция усилителя:

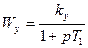, (2)

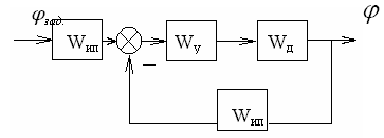
W_Д – передаточная функция двигателя постоянного тока:

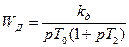. (3)

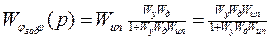(4)

Отсюда получаем:

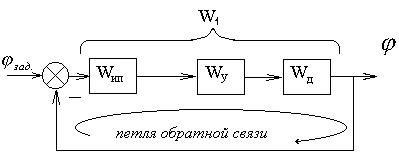
Из выражения (4) и условий (1), (2), (3) получаем характеристическое уравнение по правилу:

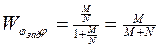M + N = 0 - характеристическое уравнение.

В результате получим характеристическое уравнение:

p T₀ (1+ p T₂) (1+ p T₁) + k_ип k_у k_д = 0

k = k_ип k_у k_д - статический петлевой коэффициент усиления

T₀ T₁ T₂ p³ + T₀(T₁ + T₂ )p + T₀ p + k = 0

По критерию устойчивости Гурвица для систем третьего порядка получаем:

T₀² (T₁ + T₂) > k T₀ T₁ T₂

k <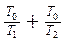

Уменьшение коэффициента усиления увеличивает запас устойчивости, но увеличивает ошибки системы.

Последнее соотношение можно отобразить на плоскости параметров, т.е. произвести D-разбиение плоскости параметров.

Если T₂ >> T₁, то k <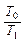

kT₁ = T₀ – граничный случай

Пусть Т₀ = 1с 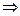kT₁ = 1

4.2.3 Теоремы Ляпунова.

Практически, при учете малых параметров системы порядок системы и полюса системы могут измениться, сделанное заключение об устойчивости может оказаться неверным.

Существует три важные теоремы Ляпунова:

1) Если все полюса исходной системы левые, то учет малых параметров не может изменить устойчивость системы.

2) Если в исходной системе имеются правые полюса, т.е. система неустойчива, то учет малых параметров не может сделать систему устойчивой.

3) Если в исходной системе имеются нейтральные полюса, то влияние малых членов неопределенно.

4.3 частотные критерии устойчивости.

Когда порядок характеристического уравнения высок, алгебраические критерии устойчивости, как правило, не дают возможность установить влияние отдельных параметров на устойчивость и получить рекомендации по выбору этих параметров. В связи с этим в 30-х годах были разработаны более приспособленные для инженерных исследований и расчетов графо-аналитические методы, использующие частотные характеристики.

В основе всех частотных критериев лежит известный из теории функций комплексного переменного принцип аргумента.

4.3.1 принцип аргумента.

Рассмотрим линейную замкнутую систему, описываемую следующим дифференциальным уравнением:

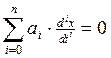(1)

Характеристическое уравнение этой замкнутой системы будет следующее:

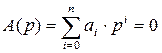(2)

Полином 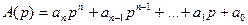называется характеристическим полиномом.

Решив характеристическое уравнение, мы получим n полюсов замкнутой системы .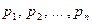

Тогда характеристический полином можно записать:

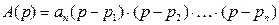(3)

Изобразим эту ситуацию на комплексной плоскости (рис. 1):

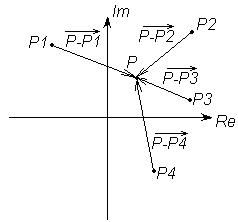
рис.1

Произведем в характеристическом полиноме замену :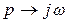

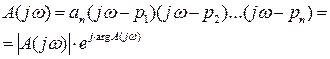(4)

Учитывая, что в данном случае переменная чисто мнимая, ситуацию можно изобразить так (р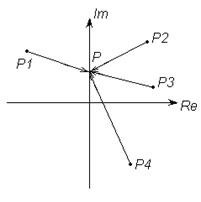ис.2):

рис.2

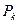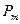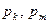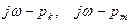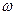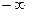Нанесем на комплексную плоскость точки , , соответствующие полюсам соответственно, и рассмотрим, как будут вести себя векторы при увеличении частоты от до 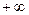. Изменение аргумента полинома 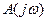в этом случае будет равно:

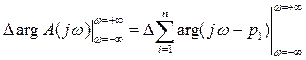(5)

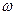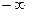Из рисунка 3 видно, что при изменении частоты от до 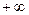начало векторов остается в точках 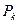, 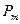соответственно, а концы перемещаются снизу вверх по всей мнимой оси, в результате чего вектор, соответствующий левому полюсу, поворачивается на угол 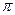против часовой стрелки, а вектор, соответствующий правому полюсу, также поворачивается на угол 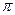, но по часовой стрелке.

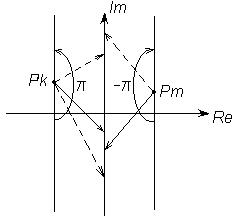
рис.3

Пусть полином имеет 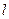правых полюсов и 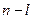левых полюсов. Тогда приращение аргумента будет равно:

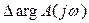
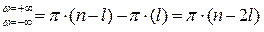(6)

Очевидно, что при изменении частоты от 0 до приращение аргумента будет вдвое меньше:

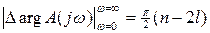(7)

В самом деле, каждый из векторов 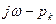, соответствующих вещественным корням, повернется теперь на угол 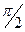или 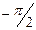, а векторы 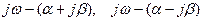, соответствующие паре сопряженных комплексных корней, один на угол 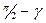, другой – на угол 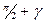, общее же приращение их аргумента будет .

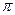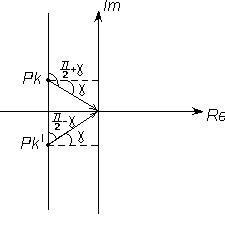
рис.4

4.3.2 критерий устойчивости михайлова.

Этот критерий был разработан Михайловым А.В. в 1938 году.

Ранее было выяснено, что для устойчивости системы необходимо и достаточно, чтобы все корни характеристического уравнения (полюса системы) были левыми. Теперь рассмотрим соотношение 7. Так как для устойчивости корни должны быть левыми, то в этом выражении должно быть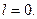

Тогда получаем:

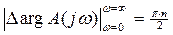(8)

Линия, которую описывает на плоскости вектор 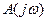(4) при изменении частоты от нуля до бесконечности называется годографом Михайлова.

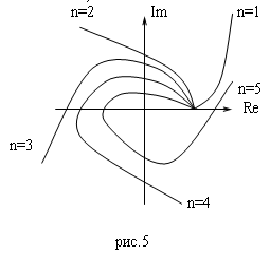
Изобразим на комплексной плоскости несколько видов годографов при различных количествах корней 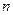(все годографы изобразим для устойчивых систем):

Так как 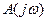можно записать в виде

,

то при получаем 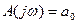, т.е. все годографы начинаются из одной точки.

Для устойчивости системы необходимо и достаточно, чтобы все корни были левыми, то есть чтобы среди них не было не только правых корней, но и лежащих на мнимой оси и обращающих в нуль функцию .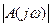

Таким образом, к необходимым и достаточным условиям устойчивости можно отнести:

1)

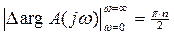
2)

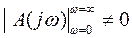
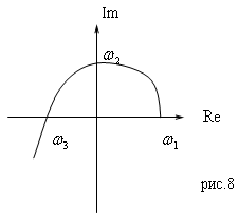
В устойчивой системе годограф Михайлова представляет собой плавную спиралевидную кривую, последовательно пересекающую квадранты комплексной плоскости и уходящую в бесконечность в квадранте, номер которого совпадает с порядком системы.

Отсюда получаем, что даже годограф, изображенный на следующем рисунке соответствует неустойчивой системе, так как, несмотря на то, что в бесконечность годограф уходит в 4-м квадранте и порядок системы тоже 4, но нарушена последовательность пересечения квадрантов.

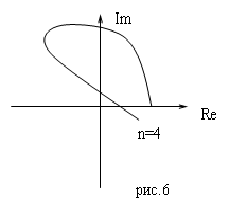
Следующая же система является устойчивой:

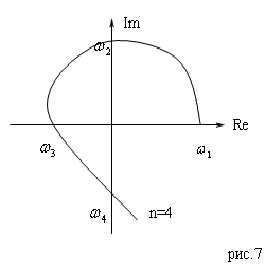
Отметим, что в не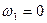й и .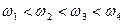

Разделим 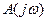на действительную и мнимую части: 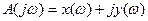. Тогда можно отметить соответствия:

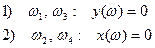
То есть получаем: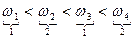

Получаем, что если выполняется условие перемежаемости корней, то система устойчива.

В завершение следует отметить, что критерий Михайлова может применяться и при порядках системы больших 4 – 5.

Пример. Для примера возьмем уже рассмотренную ранее систему слежения отработки угла.

Она имеет характеристическое уравнение:

.

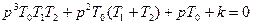Произведем замену :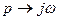

.

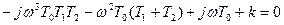Произведем разделение на мнимую и действительную части:

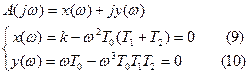
Из этой системы получаем:

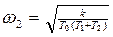(см. 9)

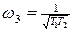(см.10)

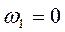(см.10)

Из условия перемежаемости корней находим значение 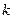, при котором система устойчива:

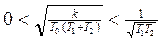
Отсюда

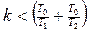
4.3.3 критерии устойчивости найквиста.

В 1932 г. Найквистом был опубликован критерий, позволяющий судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике 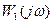разомкнутой системы. Первоначально критерий предназначался для исследования радиотехнических усилителей с обратной связью, но вскоре он получил широкое распространение для исследования устойчивости следящих систем и систем автоматического регулирования. [5]

Рассмотрим некоторую разомкнутую систему:

рис.1

Соответствующая ей замкнутая система:

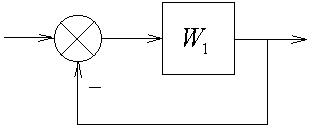
рис.2

Замыканием системы считается подача выходного сигнала с обратным знаком на вход. Как уже было сказано ранее, критерий Найквиста позволяет судить об устойчивости замкнутой системы по годографу разомкнутой системы. Рассмотрим передаточные функции систем и выясним их взаимосвязь.

Пусть передаточная функция разомкнутой системы имеет вид:

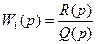. (1)

Тогда знаменатель из этой формулы будет представлять собой характеристический полином разомкнутой системы:

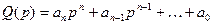. (2)

С учетом передаточной функции разомкнутой системы составим передаточную функцию замкнутой системы:

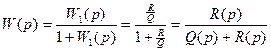. (3)

Пусть 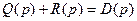, тогда 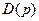- характеристический полином замкнутой системы, причем, если в выражении (1) 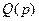имеет порядок n, а 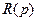имеет порядок m (m 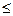n), то степени полиномов 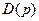и 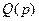одинаковы.

Введем некоторую вспомогательную функцию :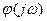

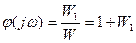. (4)

или

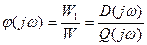. (5)

Выражение (4) получается при подстановке вместо 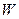выражения, которое устанавливает зависимость между 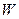и .

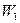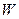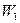Выражение (5) получается при подстановке вместо и выражений (3) [с учетом замены 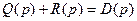] и (1) соответственно.

В выражении (4) и (5) также произведена замена .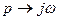

Вспомогательную функцию 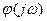можно также представить в виде:

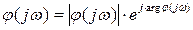
Рассмотрим изменение аргумента вспомогательной функции при изменении частоты от 0 до 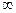. При этом, исходя из выражения (5), учтем, что аргумент частного равен разности аргументов 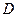и .

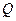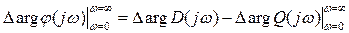(6)

Из темы о принципе аргумента известно, что если 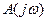- характеристический полином, то

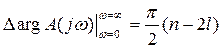, (7)

где 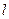- количество правых полюсов, а 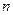- общее количество полюсов. Тогда, учитывая, что в замкнутой системе для устойчивости все полюса должны быть левыми, выражение (6) с учетом (7) преобразуется:

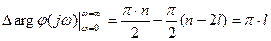(8)

Здесь 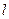- количество правых полюсов разомкнутой структуры. Отсюда делаем вывод, что для того, чтобы замкнутая структура была устойчивой годограф вспомогательной функции 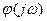должен охватывать начало координат комплексной плоскости в положительном направлении на угол 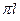. Теперь перейдем в последней формулировке от вспомогательной функции к передаточной функции разомкнутой системы.

Так как в нашей формулировке годограф вспомогательной функции охватывает начало координат, то

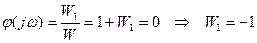
То есть мы получаем, что для устойчивости замкнутой структуры необходимо и достаточно, чтобы частотный годограф разомкнутой структуры охватывал точку с координатами (-1; 0) в положительном направлении на угол .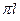

Поскольку разомкнутая система может быть устойчивой и неустойчивой, то возможно два случая. Рассмотрим их.

А) Разомкнутая система устойчива.

Так как система устойчива, то у нее все полюса левые, а значит 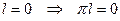. То есть мы получаем, что если разомкнутая система устойчива, то для устойчивости эквивалентной замкнутой системы годограф разомкнутой не должен охватывать точку (-1;0).

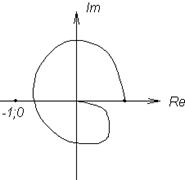
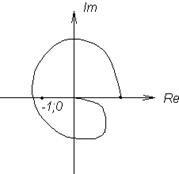
устойчивая система неустойчивая система

устойчивая система

рис.3

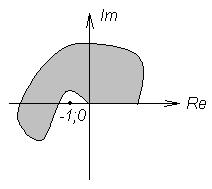
Б) Разомкнутая система неустойчива.

Так как система неустойчива, то у нее имеются правые корни, то есть .

Этот случай может возникнуть в следующих случаях:

1) местные обратные связи;

2) в разомкнутой системе есть неустойчивые звенья.

Таким образом, если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф разомкнутой системы охватывал точку (-1;0) в положительном направлении (против хода часовой стрелки) на угол .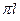



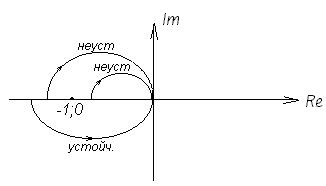
рис.5

Следует также отметить условия охвата точки (-1;0):

.

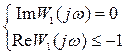Здесь 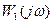- передаточная функция разомкнутой системы.

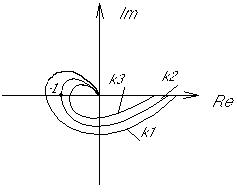
Пример. Рассмотрим трехполюсный усилитель:

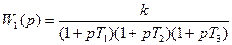
Разомкнутая система, имеющая такую передаточную функцию устойчива.

В этом случае в зависимости от значения 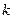можно получить различные результаты (см. рис. 6):

При 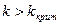система теряет устойчивость.

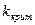можно найти из условий:

.

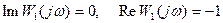Системы, которые при 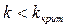устойчивы называют асимптотически устойчивыми системами. Существуют также системы, которые теряют устойчивость, как при увеличении 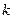, так и при его уменьшении. Такие системы называются условно устойчивыми.

Сформулируем полностью критерий Найквиста:

В системах, которые устойчивы в разомкнутом состоянии, для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал точку (-1;0). Для систем же, которые неустойчивы в разомкнутом состоянии, для устойчивости замкнутой системы годограф разомкнутой должен охватывать эту точку на угол 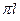в положительном направлении.

4.3.4 применение критерия найквиста для систем, находящихся в разомкнутом состоянии на границе устойчивости.

Пусть передаточная функция разомкнутой системы имеет вид:

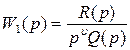(1)

Предполагается, что 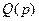имеет только левые полюса.

Наличие интегратора 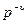свидетельствует об астатизме системы, 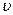- степень астатизма.

Эти системы имеют некоторые особенности по сравнению с системами, которые мы до сих пор рассматривали.

В рассмотренных ранее случаях годограф разомкнутой системы вместе с действительной осью образовывал замкнутый контур, теперь же замкнутый контур не образуется.

Для примера рассмотрим следующую передаточную функцию разомкнутой системы:

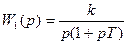
С помощью несложных преобразований эту передаточную функцию можно привести к виду:

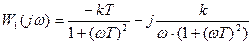
Ее годограф будет иметь вид:

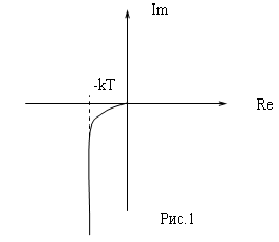
Как же определить, охватывает ли годограф точку (-1;0)? Для этого применяют следующий прием: строят дополнение годографа в бесконечности.

Другими словами, строят дугу бесконечно большого радиуса, соединяющую действительную положительную полуось с годографом в отрицательном направлении (по часовой стрелке). При этом образуется замкнутый контур и далее критерий Найквиста применяется как для системы, устойчивой в разомкнутом состоянии.

Тогда для рассматриваемого примера получаем:

Следовательно, замкнутая система устойчива.

4.3.5 применение критерия найквиста в системах, содержащих звенья с чистым запаздыванием.

Передаточная функция звена с чистым запаздыванием имеет вид:

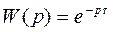(1)

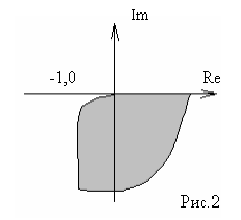
Пусть имеется следующая устойчивая система:

Пусть годограф этой системы имеет вид:

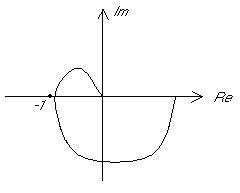
рис.2

Теперь добавим в эту систему звено запаздывания:

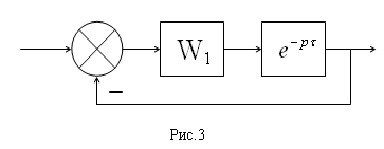
Произведем в звене запаздывания замену 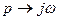. Тогда получаем:

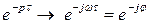
Здесь 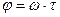. Как известно, умножение передаточной функции на эту экспоненту соответствует повороту на угол 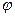вектора 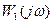. Но тогда при определенном угле поворота может создаться ситуация охвата точки (-1;0) и система станет неустойчивой. Рассмотрим эту ситуацию.

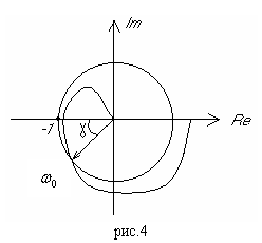
На рис.4 - запас устойчивости по фазе. Пусть 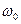- частота, при которой вектор имеет длину 1 (частота среза). Тогда при наличии множителя 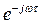лишь при изменении 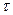может возникнуть критическая ситуация, когда указанный на рисунке вектор повернется своим концом в точку (-1;0) и замкнутая система станет неустойчивой. Отсюда получаем условие устойчивости:

.

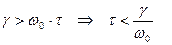4.3.6 определение устойчивости с помощью критерия найквиста по ЛАЧХ и ЛФЧХ эквивалентной разомкнутой структуры.

Возможно также определение устойчивости замкнутой структуры по логарифмическим частотным характеристикам разомкнутой структуры.

Пусть имеется некоторая разомкнутая система. Она устойчива и имеет годограф следующего вида:

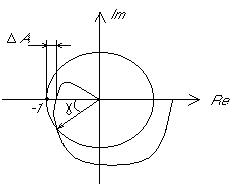
рис.1

Известно, что если разомкнутая система устойчива и ее годограф имеет такой вид (т.е. не охватывает точку (-1;0)), то замкнутая система устойчива.

Из рисунка видим, что при частоте, когда модуля вектора было достаточно для неустойчивости системы, не хватало угла 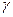, когда же угла хватало, стало недоставать модуля вектора на .

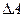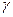- запас устойчивости по фазе.

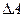- запас устойчивости по амплитуде.

Изобразим ЛАЧХ и ЛФЧХ разомкнутой структуры и, исходя из рис.1, отметим 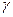и :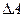

Участок, на котором выполняется условие положительности ЛАЧХ, называется участком баланса амплитуд. Частота, на которой угол сдвига фаз достигает 180⁰ – баланс фаз.

Сопоставляя годограф и ЛАЧХ, нужно отметить, что когда выполняется условие баланса амплитуд, то модуль вектора больше 1. Теперь можно сформулировать условие устойчивости по ЛАЧХ и ЛФЧХ разомкнутой системы:

Если имеется разомкнутая устойчивая система, то эквивалентная замкнутая структура будет устойчивой, если среди частот баланса амплитуд нет частоты баланса фаз.

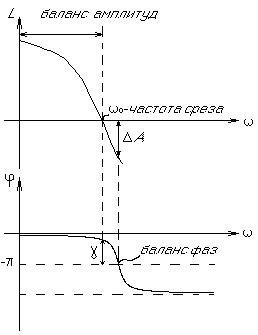
рис.2

Говоря о ЛАЧХ, следует также отметить, что при проектировании устойчивой системы автоматического управления (САУ) с достаточными запасами устойчивости, как правило, добиваются, чтобы ЛАЧХ пересекала ось частот под углом -20 .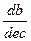

Ключевые термины и понятия.

Критерий устойчивости Гурвица. Если все диагональные миноры матрицы Гурвица положительны, то система устойчива.

Критерий устойчивости Рауса-Гурвица. Если все элементы первого столбца таблицы Рауса имеют один знак, то система устойчива.

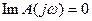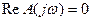Критерий устойчивости Михайлова А.В. В устойчивой системе годограф Михайлова – это плавная кривая, которая при изменении частоты от нуля до бесконечности последовательно пересекает (n-1) квадрант, уходя в бесконечность в n-ом квадранте. Вместо построения годографа часто используют признак перемежаемости корней и , где 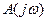- частотный характеристический полином системы.

Критерий устойчивости Найквиста Г. Позволяет судить об устойчивости замкнутой системы по годографу разомкнутой.

Теоремы Ляпунова А.М. О влиянии малых параметров на устойчивость системы.

Необходимые условия устойчивости. Все коэффициенты характеристического уравнения системы должны быть положительны.

Принцип аргумента. Лежит в основе всех частотных критериев устойчивости. Утверждает, что изменение аргумента комплексного коэффициента передачи 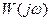при изменении частоты от нуля до бесконечности равно 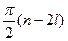, где n – порядок системы, а 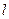– количество правых полюсов.

Устойчивая система. Система устойчива, если собственные переходные процессы являются затухающими, т.е. если все корни ее характеристического уравнения (полюса передаточной функции) имеют отрицательные действительные части.