Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b - a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.
Предельный переход в неравенствах
Теорема 1. Если 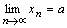 и, начиная с некоторого номера, выполняется
и, начиная с некоторого номера, выполняется 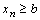
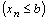 , то
, то 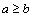
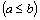 .
.
Доказательство. Пусть с некоторого номера выполняется 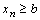 Предположим, что
Предположим, что 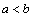 . Так как
. Так как 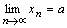 , то для
, то для 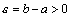 существует такой номер N, что для всех
существует такой номер N, что для всех 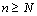 выполняется
выполняется 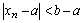 или
или 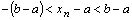 , откуда получаем
, откуда получаем 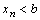 , что противоречит условию. Случай
, что противоречит условию. Случай 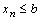 рассматривается аналогично.
рассматривается аналогично.
|
|
|
Следствие 1. Пусть 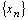 и
и  сходятся и, начиная с некоторого номера, выполняется
сходятся и, начиная с некоторого номера, выполняется 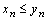 , тогда
, тогда 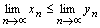 .
.
Следствие 2. Пусть 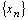 сходится и при любом
сходится и при любом 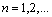
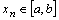 , тогда и
, тогда и 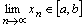 .
.
Доказательство. Так как 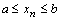 , то и
, то и 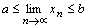 .
.
Теорема 2. Пусть 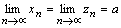 и с некоторого номера n выполняется условие
и с некоторого номера n выполняется условие 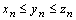 .Тогда последовательность
.Тогда последовательность  сходится и
сходится и 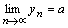 .
.
Доказательство. Пусть 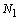 – номер, с которого выполняется
– номер, с которого выполняется 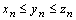 , тогда с этого номера выполняется
, тогда с этого номера выполняется 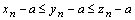 , или
, или 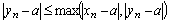 . Так как
. Так как 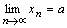 и
и 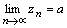 , то для любого числа
, то для любого числа 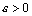 существуют такие номера
существуют такие номера 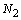 и
и 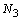 , что для всех
, что для всех 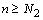
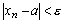 , а для всех
, а для всех 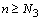
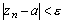 , а для всех номеров
, а для всех номеров 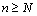 , где
, где 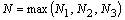 выполняется
выполняется 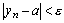 , что и означает
, что и означает 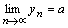



15. Бесконечно малые и бесконечно большие функции.


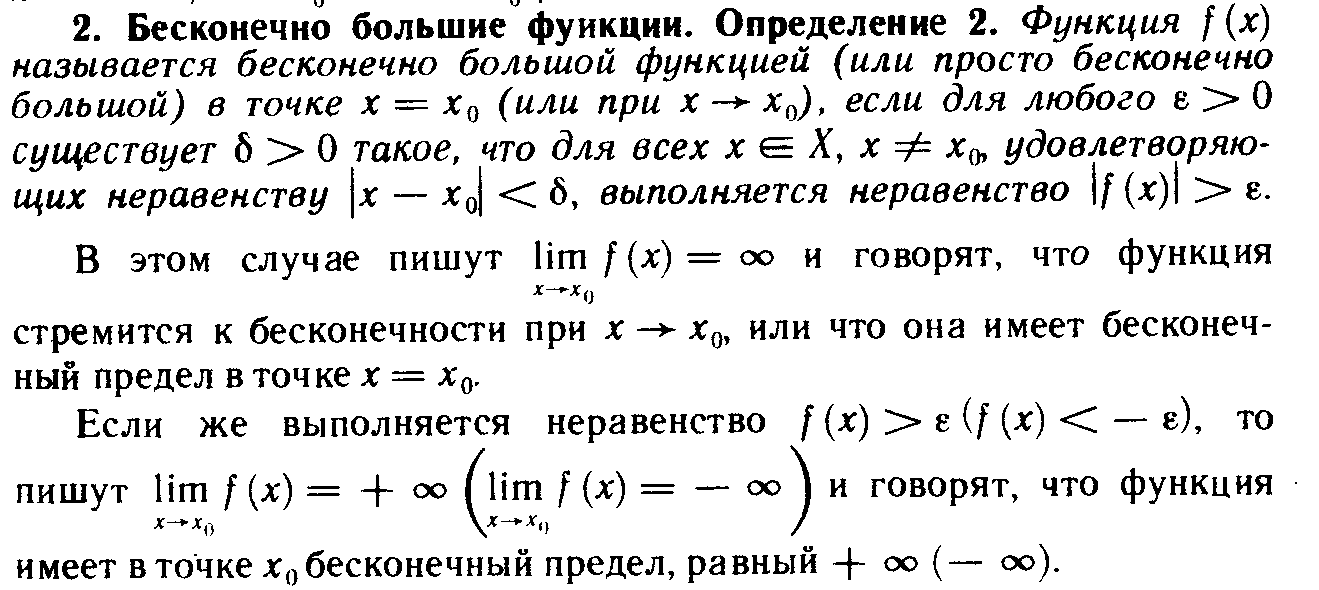

 2015-04-20
2015-04-20 15096
15096








