Теорема 2.5 тогда общее решение даётся формулой

1) Если корни 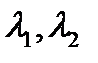характеристического уравнения (2.7) действительные числа

и 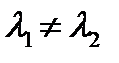тогда общее решение даётся формулой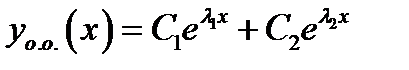

2) Если корни 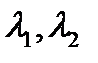характеристического уравнения (2.7) действительные числа

и 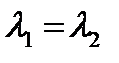тогда общее решение даётся формулой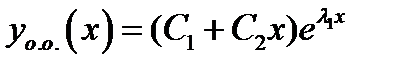

3) Если корни 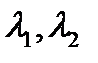характеристического уравнения (2.7) комплексные числа

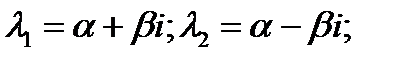тогда общее решение даётся формулой

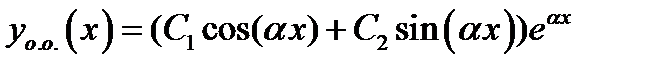
Доказательство. Нужно проверить, что данные функции 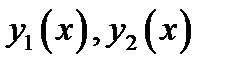являются решениями и выполняются условия (2.3). Проверим, например, второй пункт теоремы 2.5. Пусть

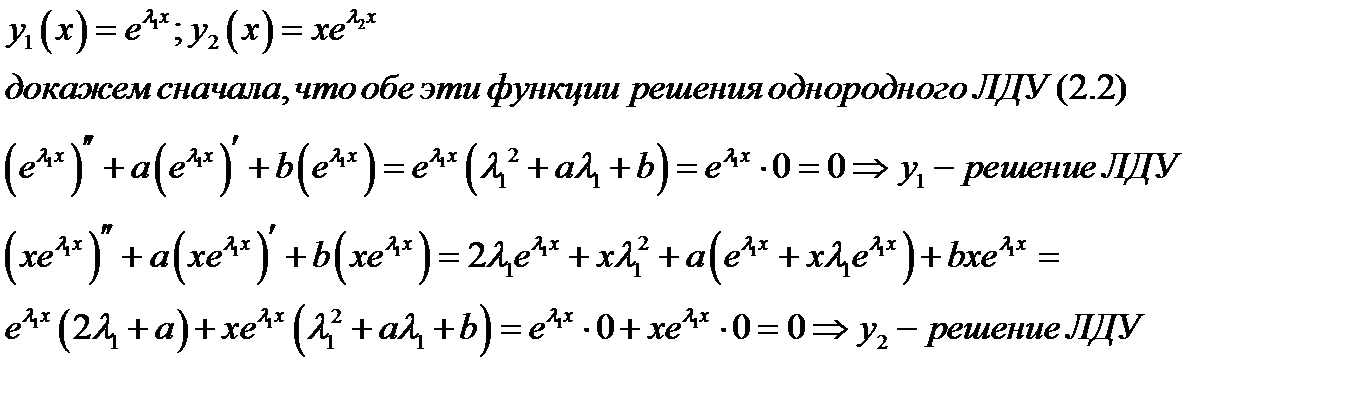
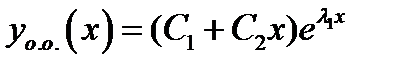
Пункты 1и 3 проверяются аналогично.

Контрольные вопросы.

I. Какое ОДУ называется уравнением второго порядка, третьего порядка, n-го орядка?

II. Как ставится начальная задача Коши для ОДУ второго порядка?

III. Определите типы уравнений второго порядка, допускающих понижение порядка.

IV. Приведите правила нахождения общих решений таких уравнений.

V. Определите линейное ОДУ второго порядка а) однородное, б) неоднородное.

VI. Какие функции на интервале 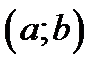называются линейно а) зависимыми, б) независимыми?

VII. Какая функция называется решением начальной задачи неоднородного ЛДУ?

VIII. Как определяется общее решение неоднородного ЛДУ.

IX. Как определяется линейная независимость частных решений ЛДУ.

X. Какие однородные ЛДУ можно решать с помощью характеристического уравнения?

Дайте определение фундаментальной системы решений ЛДУ. Какой вид имеет общее решение ЛДУ второго порядка а) однородного, б) неоднородного