Определение 2.1. Неоднородным ЛДУ второго порядка назовём уравнение вида
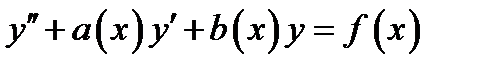 (2.1)
(2.1)
где 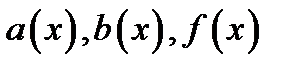 заданные непрерывные функции от
заданные непрерывные функции от  . Если
. Если  , то уравнение назовём однородным
, то уравнение назовём однородным
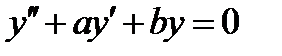 (2.2)
(2.2)
Пусть 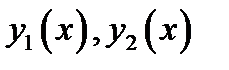 являются решениями однородного ЛДУ (2.2)
являются решениями однородного ЛДУ (2.2)
Определение 2.2. Функции 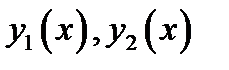 назовём линейно зависимыми если
назовём линейно зависимыми если
либо 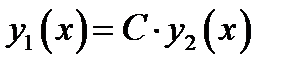 , либо
, либо 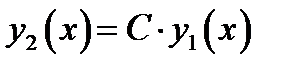 , где С постоянная величина
, где С постоянная величина
в противном случае функции 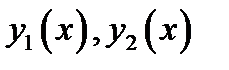 называются линейно независимыми.
называются линейно независимыми.
Теорема 2.1. Функции 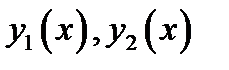 будут линейно независимыми, если выполняются
будут линейно независимыми, если выполняются
условия:
1) являются решениями ЛДУ (2.2)
2) определитель Вронского
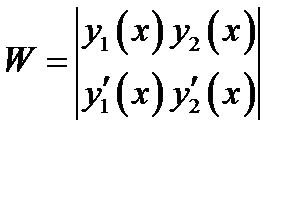
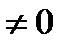 . (2.3)
. (2.3)
Определение 2.3. Решением начальной задачи назовём функцию удовлетворяющую условиям
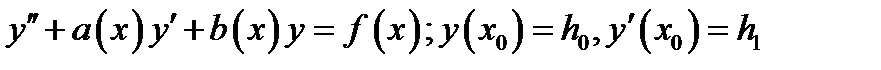 (2.4)
(2.4)
где 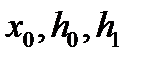 произвольно заданные числа. Условия
произвольно заданные числа. Условия 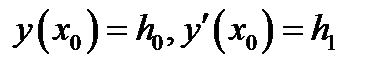 называются начальными условиями.
называются начальными условиями.
Теорема 2.2. Если в ЛДУ (2.1) коэффициенты 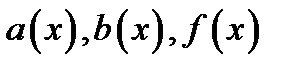 непрерывны на интервале
непрерывны на интервале 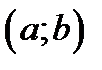 и
и 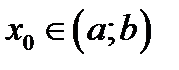 , то для любых чисел
, то для любых чисел 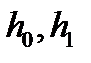 решение начальной задачи существует в единственном экземпляре.
решение начальной задачи существует в единственном экземпляре.
Определение 2.4. Общее решение неоднородного ЛДУ (2.1) является объединением решений
произвольных начальных задач.
Определение 2.5. Любое конкретное решение неоднородного ЛДУ (2.1) назовём частным решением неоднородного уравнения.
Теорема 2.3. Если 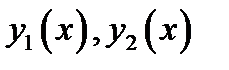 линейно независимые решения однородного ЛДУ (2.2), то общее решение однородного ЛДУ дается формулой
линейно независимые решения однородного ЛДУ (2.2), то общее решение однородного ЛДУ дается формулой
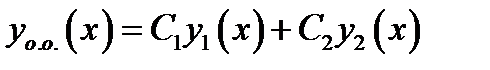 (2.5)
(2.5)
Здесь 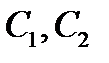 произвольные постоянные.
произвольные постоянные.
Доказательство. Нужно доказать два факта
1) 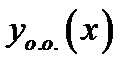 является решением однородного ЛДУ (2.2)
является решением однородного ЛДУ (2.2)
2) любое решение начальной задачи можно получить из формулы (2.5) подбором
постоянных.
Проверим выполнение пункта 1). По условию 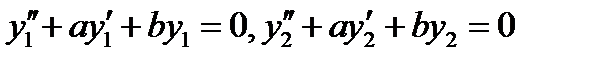 . Далее
. Далее
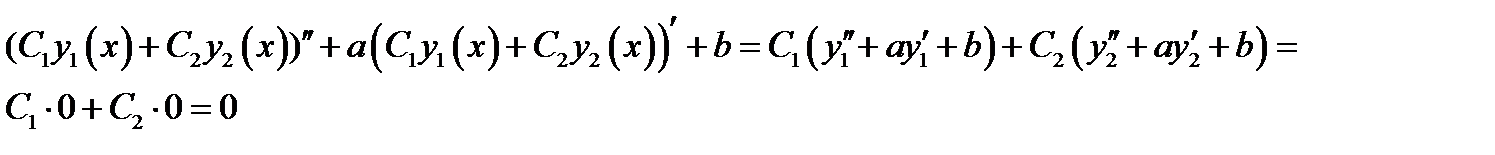
первый пункт теоремы доказан.
Докажем второй пункт. Пусть 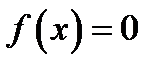 и
и 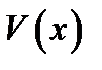 является решением задачи Коши (2.4). Берём общее решение
является решением задачи Коши (2.4). Берём общее решение 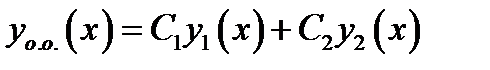 и докажем, что можно подобрать постоянные
и докажем, что можно подобрать постоянные 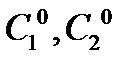 такие, что
такие, что 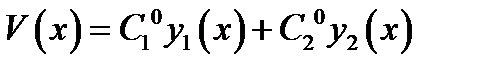 . То, что
. То, что 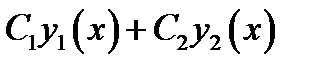 решение однородного ЛДУ доказано в пункте 1). Осталось подобрать постоянные
решение однородного ЛДУ доказано в пункте 1). Осталось подобрать постоянные 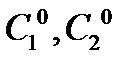 , чтобы выполнялись начальные условия.
, чтобы выполнялись начальные условия.
Используя начальные данные (2.4) решаем систему уравнений с искомыми неизвестными 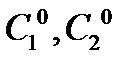

Теорема 2.3 доказана. Пара решений 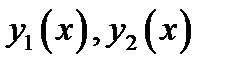 однородного ЛДУ, удовлетворяющих условию (2.3) называется фундаментальной системой решений (ФСР).
однородного ЛДУ, удовлетворяющих условию (2.3) называется фундаментальной системой решений (ФСР).
Итак, если функция 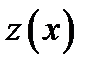 является решением однородного ЛДУ (2.2), то можно подобрать постоянные
является решением однородного ЛДУ (2.2), то можно подобрать постоянные 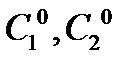 так, что
так, что 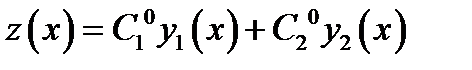 . Здесь
. Здесь 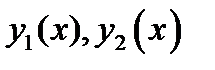 образуют ФСР.
образуют ФСР.
 2015-04-30
2015-04-30 358
358








