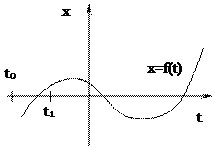Дихотомия (метод деления пополам)

Пусть найдены такие точки t₀ и t₁, что 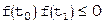, то есть на отрезке [t₀,t₁] лежит не менее одного корня уравнения .

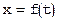Найдем середину отрезка 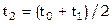и вычислим 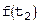. Из двух половин отрезка выберем ту, для которой 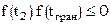. Эту половину делим пополам и выбираем ту половину, на концах которой функция имеет разные знаки.

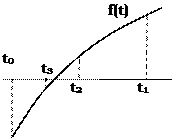Если требуется найти корень с точностью e, то продолжаем деление пополам до тех пор, пока длина отрезка не станет меньше 2e. Тогда середина последнего отрезка даст значение корня с требуемой точностью.

Дихотомия проста и очень надежна: к простому корню она сходится для любых непрерывных функций 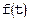, в том числе недифференцируемых. Дихотомия устойчива к ошибкам округления, скорость сходимости невелика: за одну итерацию точность увеличивается примерно вдвое, то есть уточнение трех цифр требует 10 итераций (2¹⁰~1000). Но точность результата гарантируется.

Недостатки метода:

Для начала вычислений надо найти отрезок, на котором функция меняет знак;

Если в этом отрезке несколько корней, то неизвестно, к какому из них сойдется процесс;

На системы уравнений дихотомия не обобщается.

Пример. Решить уравнение 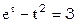с точностью до e = 0.1.

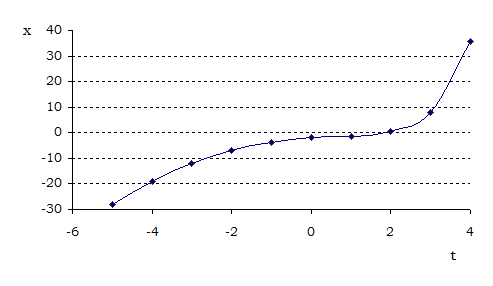
Построим график функции :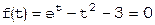

Из графика следует, что уравнение имеет единственный корень вблизи t=2. Поэтому выберем отрезок [1.5,2], на концах которого функция меняет знак.

f(t₀)<0, f(t₁)>0, t₀=1.5, t₁=2, t₂=(1.5+2)/2=1.75

f(t₂)=f(1.75)=-0.308<0;

f(t₂)<0, f(t₁)>0, t₂=1.75, t₁=2, длина отрезка 0.25, t₃=(1.75+2)/2=1.88

f(t₃)=f(1.88)=0.019>0;

f(t₃)>0, f(t₂)<0, t₃=1.88, t₂=1.75, длина отрезка 0.13, t₄=(1.88+1.75)/2=1.82

0.13<2e = 0.2, поэтому с требуемой точностью корень уравнения 1.82.

(С точностью до 4-х знаков после точки корень равен 1.8731).