Эконометрика. 1. Экономет. Модели, их виды

1. Экономет.модели, их виды. В.переменных и типы данных в экономет. исследованиях. Гл. инструментом экономет. исследования явл. модель. Выделяют три осн. класса экономет. моделей: 1) модель временных рядов (МВР); 2) модели регрессии с одним уравнением; 3) СИ одновременных уравнений.

МВР - завис-ть результ. переменной от переменной времени или переменных, относящихся к др. моментам времени.(если каждый месяц измерять и записывать кол-во потребленной энергии, то образуется ряд чисел, кот. и представляет собой врем. ряд. Здесь переменная времени – это дата (t), а результ. переменная – кол-во потребленной энергии (y). Математически это записывается как y = f (t), т.е. зависимость кол-ва потребленной энергии от времени). К МВР, характер-щих завис-ть результат.переменной от времени, относятся: а) модель завис-ти результ. переменной от трендовой компоненты или модель тренда (тренд – иначе тенденция, это может быть постепенное возрастание и убывание значений результ.переменной за все время наблюдений); б) модель завис-ти результативной переменной от сезонной компоненты или модель сезонности (значения в ряду то нарастают, то убывают с определенной периодичностью); в) модель завис-ти результат. переменной от трендовой и сезонной компонент или модель тренда и сезонности. К МВР, характер-щих завис-ть результ. переменной от переменных, датированных др. моментами времени, относятся: а) модели с распред. лагом (лаг – это сдвиг по времени), объясняющие вариацию результ. переменной в завис-ти от предыдущих значений фактор.переменных (это переменные, кот. помимо времени влияют на рез-т.(цена (х) влияет на спрос(у)). В такой модели каждое последующее значение спроса зависит от цен, кот. были раньше); б) модели авторегрессии, объясняющие вариацию результ. переменной в завис-ти от предыдущих значений результ. перемен. (в такой модели уже на спрос, т.е. на кол-во продан. товара в данн.момент, влияет сам спрос, но в предыдущие моменты времени); в) модели ожидания, объясняющие вариацию результ. переменной в завис-ти от будущ.значений факторных или результ. переменных (то же, что в моделях а) и б), но влияют не предыдущие, а последующие значения). МВР делятся на модели, построенные по: стационарным и нестационарным времен. рядам. Стац. врем.рядом называется времен. ряд, кот. характер-ся постоян. во времени средней, дисперсией и автокорреляцией, т. е. данн.временной ряд не содержит трендовой и сезонной компонент. Нестац.врем. рядом называется врем. ряд, кот.содержит трендовую и сезонную компоненты.

Модель регрессии с одним уравнением называется завис-ть результат. переменной, обозначаемой как у, от факторных (независимых) переменных, обозначаемых как х ₁ ,х ₂ ,…,х _n (ст-ть подержанного автомобиля (это у) зависит от срока эксплуатации (х₁), пробега (х₂) и т.п.). Данн.завис-ть можно представить в виде функции регрессии или модели регрессии: y=f(x,β)=f(х ₁ ,х ₂ ,…,х _n, β ₁ …β _k ) где β ₁ …β _k– параметры модели регрессии.

Можно выделить 2 осн. классиф. моделей регрессии: а) классификация моделей регрессии на парные (один у и один х, вместе – пара переменных) и множественные регрессии в завис-ти от числа факторных переменных; б) классиф. моделей регрессии на линейные (описываются уравнениями прямой линии) и нелинейные регрессии в завис-ти от вида функции f(x,β).

СИ одновременных уравнений - модель, кот. описывается СИ взаимозависимых регресс. уравнений. СИ одновр. уравнений могут включ.в себя тождества и регресс.уравнения, в кажд. из кот. могут входить не только факторные переменные, но и результ. переменные из др.уравнений СИ. Регресс. уравнения, входящие в СИ одновременных уравнений, называются поведенческими уравнениями (ПУ). В ПУ значения параметров явл. неизвестными и подлежат оцениванию.

Переменные и данные. В экономет. моделях в осн. используются данные 3 типов: 1) пространственные данные; 2) временные ряды; 3) панельные данные.

Простран. данными называется совок-ть эк. инф-ции, кот. характ-ет различ. объекты, однако полученной за один и тот же период или момент времени. Примером пространственных данных может служить комплекс эк. инф-ции по какому-либо пред-тию (численность работников, V пр-ва, размер основных фондов), объёмах потребления пр-ции опред. вида, данные о ВВП различ.стран в каком-либо конкретном году и т. д.

Временными данными называется совок-ть эк. инф-ции, кот. характер-ет один и тот же объект, но за разные периоды времени.

Отдельно взятый временной ряд можно рассматривать как выборку из бесконечного ряда значений показателей во времени. Примером временных данных могут служить данные о динамике индекса потреб. цен, ежедневные обменные курсы валют.

Панельными данными называются данные, содержащие сведения об одном и том же множестве объектов за ряд последовательных периодов времени. Панельные данные явл. обобщением или комбинацией пространственных и временных данных. Примером панельных данных могут служить показатели хоз. деят-ти совокупности пред-тий, кот. собираются каж.год.

В экономет. моделировании выделяют след. виды эк. переменных: 1) экзогенные или независимые переменные (х), значения кот. задаются извне. В определ. степени экзогенные переменные поддаются управлению; 2) эндогенные или зависимые переменные (у), значения кот. определяются внутри модели; 3) лаговые переменные – это экзогенные или эндогенные переменные, кот. относятся к предыдущим моментам времени и находятся в эконометр. модели одновременно с переменными, относящимися к текущему моменту времени. Например, x _t-1 – это лаговая экзогенная переменная, а y _t-1 – это лаговая эндогенная переменная; 4) предопределённые или объясняющие переменные – это лаговые (x _t-1) и текущие (х) экзогенные переменные, а также лаговые эндогенные переменные (y _t-1). 5) фиктивные переменные используются в экономет. моделях для характер-ки явления или процесса, в отношении кот. нет данных по качест. признаку; 6) переменные-заместители искусственно

вводятся в экономет. модель для характер-ки явления или процесса, кот. не может быть количественно охарактеризован. При этом переменная-заместитель тесно коррелирует с этим явлением (т.е. изменяется при его изменениях).

2.Линейные уравнения регрессии (класс. модель) (т.е.уравнения прямой линии). Общий вид нормальной (традиционной или класс.) линейной модели парной (однофакторной) регрессии: y_i=β₀+β₁x_i+ε_i, где y_i – результативные переменные, 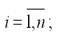x_i – факторные переменные, 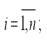β₀, β₁ – параметры модели регрессии, подлежащие оцениванию; ε_i – случайная ошибка модели регрессии.

При построении нормальной линейной модели парной регрессии учитываются 5 условий: 1) факторная переменная x_i – неслучайная или детерминированная величина, кот.не зависит от распределения случайной ошибки модели регрессии ε_i; 2) матем. ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях: 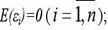3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений: 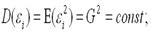4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых 2 разных наблюдений равна нулю): Cov(ε_i,ε_j)=E(ε_i,ε_j)=0. Это условие выполняется в том случае, если исходные данные не являются временными рядами; 5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: ε_i~N(0, G2).

Общий вид нормальной линейной модели парной регрессии в матричной форме:

Y= X×β+ ε,

где

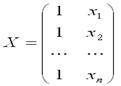
– случайный вектор-столбец значений результативной переменной размерности n ×1;

– матрица знач-й фактор. переменной размерности n ×2.

Первый столбец явл. единичным, потому что в модели регрессии коэфф. β₀ умножается на единицу;

– вектор-столбец неизвестных коэфф. модели регрессии размерности 2 × 1;

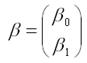
– случайный вектор-столбец ошибок модели регрессии размерности n × 1.

Условия построения норм. лин. модели парной регрессии, записанные в матрич.форме:

1) факторная переменная x_i – неслучайная или детерминированная величина, кот. не зависит от распред-ния случайной ошибки модели регрессии β_i; 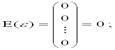2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях; 3) третье и четвёртое условия можно записать через ковариационную матрицы случайных ошибок нормальной линейной модели парной регрессии:

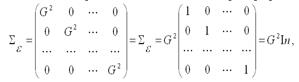
где G2 – дисперсия случайной ошибки модели регрессии ε; In – единичная матрица размерности n × n.

Ковариация - показатель тесноты связи между переменными х и у, кот. рассчитывается по формул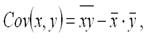е: где 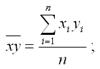– среднее арифм. знач-е произведения фактор. и результативного признаков;

Осн.свойствами показ-ля ковариации явл.: а) ковариация переменной и константы равна нулю, т. е. cov(x,C)=0 (C=const); б) ковариация переменной с самой собой равна дисперсии переменной, т. е. Cov(ε,ε)=G2(ε). По этой причине на диагонали ковариационной матрицы случ. ошибок нормальной линейной модели парной регрессии располагается дисперсия случ. ошибок; 4) случ. ошибка модели регрессии подчиняется нормальному закону распределения: εi~N(0, G2).

3.Метод наименьших квадратов (МНК). Определение коэфф. линейной регрессии по МНК. Класс. подход к оцениванию параметров лин. модели регрессии (т.е. к определению числового значения коэфф. а₀, а₁, …, а_n) основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при кот. сумма квадратов отклонений фактич.значений результативного признака 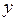от расчетных 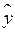минимальна: 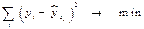. Модель регрессии или уравнение регрессии позволяет количест. оценить взаимосвязь между исследуемыми переменными.

Рассмотрим на примере парной регрессии. Оценка параметров парной регрессии производится путем миним.показателя .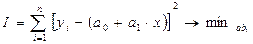

Необходимым условием минимума функции 2-х переменных явл. равенство нулю ее частных производных 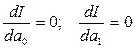. Приравнивая частные производные к нулю и сокращая на 2, получаем СИ двух лин.урав-ний с двумя неизвестными a₀ и a₁: Раскрывая скобки, и после соответствующих преобразований получаем: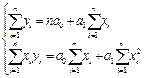

Эти уравнения называются нормальными уравнениями, решение которых дает искомые значения a₀ и a₁. Для уравнения множественной регрессии вида 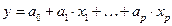СИнормальных уравнений образуется также путем миним. суммы квадратов отклонений стат. знач-я результативного признака от его прогнозного значения, рассчитанного с помощью выбранного уравнения регрессии: 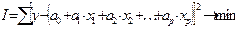здесь y – стат. знач-е результ. признака.

Если продифференцировать параметр I последовательно по кажд.коэфф.: a₀, а₁, а₂,…, а_p и приравнять полученные производные нулю, то получим следующую СИ уравнений: 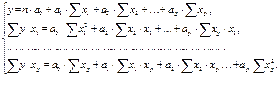Решив СИ уравнений одним из известных способов, получим параметры регрессии.

4.Нелин. регрессия, ее виды, приведение к лин. виду. Оценка параметров нелин. регрессии для урав-ния второй степени. Если между эк. явл-ми существуют нелин. соотношения, то они выражаются с помощью соответ. нелин. функций. Различают 2 класса нелин.регрессий: 1) Регрессии, нелин.относительно включенных в А объясняющих переменных, но лин. по оцениваемым параметрам, (полиномы различ.степеней – 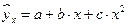, 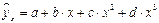; – равносторонняя гипербола – 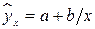; – полулогарифмическая функция – 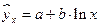.) 2) Регрессии, нелин. по оцениваемым параметрам, (– степенная – 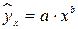; – показательная – 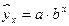; – экспоненциальная – ).

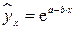Регрессии нелин. по включенным переменным приводятся к лин. виду простой заменой переменных, а дальнейшая оценка параметров произв-ся с помощью МНК. Рассмотрим некот. функции. Равносторонняя гипербола 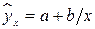может быть использована для характер-ки связи удельных расходов сырья, материалов, топлива от V выпуск. пр-ции, времени обращения товаров от величины товарооборота, % прироста заработной платы от уровня безработицы (например, кривая А.В. Филлипса), расходов на непрод. товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в др.случаях. Гипербола приводится к лин.урав-нию простой заменой: 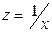. Аналогичным образом приводятся к лин.виду завис-ти 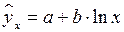, 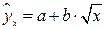и другие. Парабола второй степени 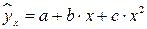приводится к лин. виду с помощью замены: 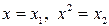. В рез-те приходим к двухфакторному уравнению 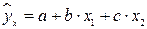, оценка параметров кот. производится при помощи МНК.

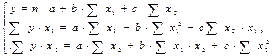Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.

5.Гетероскедастичность, ее эк. причины и методы выявления. Гетероскедастичность - неоднородность наблюдений, выраж. в неодинаковой (непостоянной) дисперсии случ.ошибки регресс. (эконом.) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случ. ошибок модели. При оценке параметров уравнения регрессии применяется МНК. При этом делаются опред. предпосылки относительно случайной составляющей 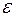. В модели

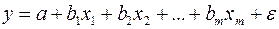случайная составляющая 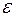представляет собой ненаблюдаемую величину. После того как произведена оценка параметров модели, рассчитывая разности факт. и теорет. знач-ний результативного признака 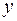, можно определить оценки случайной составляющей 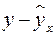. Своими словами: есть некот. данные – допустим по некот. однородным пред-тиям собраны сведения о том: - какой у них V выпуска пр-ции в год (у), - какова ст-ть осн. произв. фондов на этих пред-тиях (х ₁); - какова численность осн. произв. рабочих (х ₂). Мы предположили, что завис-ть выпус-ка от размера фондов и числен-ти линейная, т.е. описывается уравнением 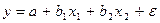Добавочка ε называется случайной составляющей и означает, что есть некот. отклонение наших фактических данных (у) от тех, которые мы рассчитаем по уравнению, когда найдем МНК параметры а, b ₁ и b ₂. Это отклонение означает, что есть др. факторы кроме ст-ти ОФ и численности работников, кот. влияют на выпуск, но мы их не учли в уравнении. Возможны также неточности в исходных данных. Если обозначить теоретические значения выпуска, т.е. рассчитанные по формуле как 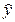, получим 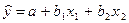. Тогда нашу модель можно записать так: 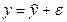, а отсюда получаем 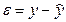. Это и есть отклонения факт. значений от теорет. их еще называются остатками. Для того, чтобы полученная нами теоретическая модель была хор. кач-ва, т.е. мы могли бы ее использовать для прогноза не опасаясь больших ошибок, проводится исследование этих остатков. Требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для кажд. значения фактора 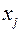остатки 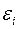имеют одинаковую дисперсию (рассеяние относительно сред. значения). Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции.

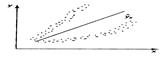
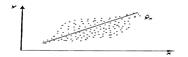
Примеры гетероскедастичности. На рис. 1 изображено: а – дисперсия остатков растет по мере увеличения 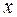; б – дисперсия остатков достигает макс. величины при сред.значениях переменной 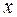и уменьшается при миним. и макс. значениях 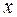; в – макс. дисперсия остатков при малых значениях 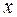и дисперсия остатков однородна по мере увеличения значений . Гетероскедастичность становится проблемой, когда значения переменных, входящих в уравнение регрессии, часто значительно различаются в разных наблюдениях. Если истинная зависимость описывается уравнением 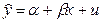, причем эк. переменные меняют свой масштаб одновременно, то изменения значений не включенных переменных и ошибки измерения, влияя совместно на случайный член, делают его сравнительно малым при малых у и х и сравнительно большим — при больших у и х. П: Мы пользуемся моделью парной регрессии для рассмотрения завис-ти между гос. расходами на образование (у) и ВВП (х) в разл. странах, и вы сделали выборку наблюдений, включающую как малые страны, такие как Сингапур, так и очень большие, такие как США. Доля гос. расходов на образование в ВВП обычно находится в диапазоне 3-9%; по-видимому, отдел.страны уделяют больше внимания частному образованию, чем другие, или правительства одних стран в большей степени, чем правительства других, осознают необходимость образования. По соц. или иным причинам та или иная страна тратит на образование долю ВВП, кот. может колебаться в пределах до 3% выше или ниже нормы. Очевидно, что при большом объеме ВВП изменение на 1% его абсолютной величины будет выражаться значительно большими цифрами, чем при малом. Также гетероскедастичность может проявиться при А данных, кот. увеличиваются со временем. (П: при исследовании завис-ти спроса от доходов населения очевидно, что как доходы, как и цены на товары и услуги могли просто возрасти со временем, и дисперсия случайной составляющей тоже может со временем увеличиваться). Для обнаружения гетероскедастичности обычно используют 3 теста, в кот. делаются различные предположения о завис-ти между дисперсией случ. члена и объясняющей переменной: тест ранговой корреляции Спирмена, тест Голдфельда - Квандта и тест Глейзера Доугерти. Тест ранговой корреляции Спирмена – тест на гетероскедастичность, устанавливающий, что стандартное отклонение остаточного члена регрессии имеет нестрогую лин.завис-ть с объясняющей переменной.

Данные по x и остатки упорядочиваются, и коэфф.ранговой корреляции определяется как: 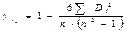где 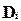- разность между рангом x и рангом 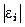. Нулевая гипотеза об отсутствии гетероскедастичности будет отклонена при заданном уровне значимости a, если она превысит критич. значение коэфф.корреляции Спирмена (т.е. рассчитанное значение сравнивается с табличным. Если рассчитанное больше, то гетероскедастичность есть). В тесте Голдфелда — Куандта, как правило, используется предположение о прямой зависимости дисперсии ошибки (остатка) от величины некоторой независимой переменной. Схема применения этого теста такова. Сначала данные упорядочиваются по убыванию той независимой переменной, относительно кот. имеется подозрение на гетероскедастичность. Затем в этом упорядоченном наборе данных исключают несколько сред.наблюдений, где несколько означает примерно четверть (25%) от общего количества всех наблюдений. Далее проводятся две независимые регрессии для первых из оставшихся (после выполненного исключения) средних наблюдений и двух последних из этих оставшихся средних наблюдений. После этого строятся два соответствующих остатка. Наконец, составляется F-статистика Фишера и, если верна исследуемая гипотеза, то F действительно явл. распределением Фишера с соответствующими степенями свободы. Тогда большая величина этой статистики означает, что проверяемую гипотезу необходимо отвергнуть. Без шага исключения наблюдений мощность данного теста уменьшается.

6.Обобщенный метод наименьших квадратов и его свойства. При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный МНК заменять обобщенным МНК. ОМНК применяется к преобразованным данным и позволяет получать оценки, кот. обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Использование ОМНК для корректировки гетероскедастичности. Как и раньше, будем предполагать, что ср. знач-е остаточных величин равно нулю. А вот дисперсия их не остается неизменной для разных значений фактора, а пропорциональна величине 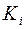, т.е. 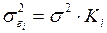, где 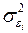– дисперсия ошибки при конкретном 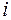-м значении фактора; 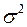– пост. дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; 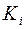– коэфф. пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.

При этом предполагается, что 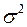неизвестна, а в отношении величин 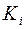выдвигаются опред. гипотезы, характеризующие структуру гетероскедастичности. В общем виде для урав-ния 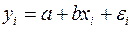при 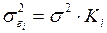модель примет вид: 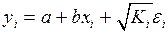. В ней остат.величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к урав-нию с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе 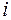-го наблюдения, на 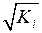. Тогда дисперсия остатков будет величиной пост., т. е. 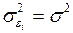. Иными словами, от регрессии 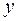по 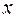мы перейдем к регрессии на новых переменных: 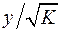и 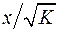. Урав-ние регрессии примет вид: 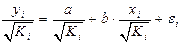, а исх. данные для данн.урав-ния будут иметь вид: 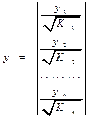, 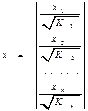.По отношению к обычной регрессии урав-ние с новыми, преобразованными переменными представляет собой взвешенную регрессию, в кот.переменные 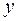и 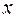взяты с весами 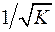. Оценка параметров нов. уравнения с преобразованными переменными приводит к взвешенному МНК, для кот. необходимо миним. сумму квадратов отклонений вида 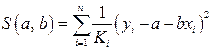.Соответственно получим след.СИ норм. урав-ний: 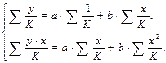Если преобразованные переменные 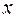и 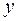взять в отклонениях от сред.уровней, то коэфф. регрессии 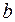можно определить как 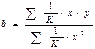.При обычном применении МНК к урав-нию лин. регрессии для переменных в отклонениях от сред.уровней коэфф.регрессии 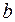определяется по формуле: 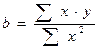. Как видим, при использовании 0МНК с целью корректировки гетероскедастичности коэфф. регрессии 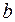представляет собой взвешенную величину по отношению к обычному МНК с весом .

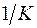Аналогичный подход возможен не только для урав-ния парной, но и для множест. регрессии. Предположим, что рассматривается модель вида 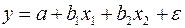, для кот.дисперсия остат.величин оказалась пропорциональна 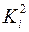. 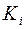представляет собой коэфф. пропорциональности, принимающий различ. значения для соответствующих 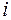значений факторов 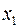и 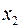. Ввиду того, что 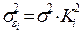, рассматриваемая модель примет вид 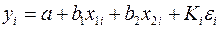, где ошибки гетероскедастичны. Для того чтобы получить уравнение, где остатки 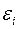гомоскедастичны, перейдем к новым преобразованным переменным, разделив все члены исходного урав-ния на коэфф.пропорциональности 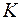. Урав-ние с преобразованными переменными составит 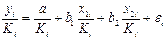. Это урав-ние не содержит свобод. члена. Вместе с тем, найдя переменные в нов. преобразованном виде и применяя обычный МНК к ним, получим иную спецификацию модели: 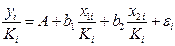. Параметры такой модели зависят от концепции, принятой для коэфф. пропорциональности 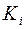. В экономет. исследованиях довольно часто выдвигается гипотеза, что остатки 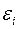пропорциональны значениям фактора. Так, если в урав-нии 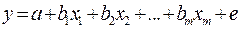предположить, что 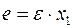, т.е. 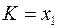и 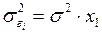, то ОМНК предполагает оценку параметров след. трансформированного уравнения: 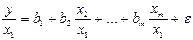. Применение в этом случае ОМНК приводит к тому, что наблюдения с меньш.значениями преобразованных переменных 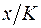имеют при определении параметров регрессии относит.больший вес, чем с первонач.переменными. Вместе с тем, следует иметь в виду, что нов. преобразованные переменные получают нов. эк. содержание и их регрессия имеет иной смысл, чем регрессия по исх. данным. П: Пусть 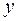– издержки пр-ва, 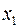– V пр-ции, 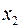– осн.произв. фонды, 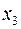– численность работников, тогда урав-ние

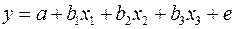явл. моделью издержек пр-ва с объемными факторами. Предполагая, что 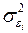пропорциональна квадрату численности работников 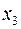, мы получим в кач-ве результативного признака затраты на 1 работника 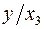, а в кач-ве факторов след. показатели: производ. труда 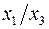и фондовооруженность труда 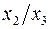. Соответственно трансформированная модель примет вид 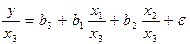, где параметры 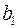, , 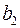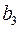численно не совпадают с аналог.параметрами предыдущей модели. Кроме этого, коэфф. регрессии меняют эк. содержание: из показателей силы связи, характеризующих сред. абсол. изменение издержек пр-ва с изменением абсол.величины соответствующего фактора на ед-цу, они фиксируют при обобщенном МНК сред. изменение затрат на работника; с изменением производит. труда на ед-цу при неизменном уровне фовдовооруженности труда; и с изменением фондовооруженности труда на ед-цу при неизменном уровне производит. труда. Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату V пр-ции, 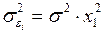, можно перейти к урав-нию регрессии вида 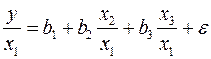. В нем новые переменные: 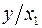– затраты на ед-цу (или на 1 руб. пр-ции), 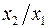– фондоемкость пр-ции, 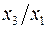– трудоемкость пр-ции. Гипотеза о пропорциональности остатков величине фактора может иметь реальное основание: при обработке недостаточно однородной совокупности, включающей как крупные, так и мелкие пред-тия, большим объемным значениям фактора может соответствовать большая дисперсия результативного признака и большая дисперсия остат. величин. При наличии одной объясняющей переменной гипотеза 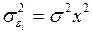трансформирует лин. урав-ние 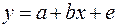в урав-ние 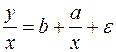, в кот.параметры 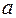и 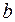поменялись местами, константа стала коэфф. наклона линии регрессии, а коэфф. регрессии – свободным членом.