После построения линейной модели регрессии, проводится проверка значимости как уравнения (модели) в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии — значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, реальным статистическим данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Проверка значимости уравнения регрессии в целом дается с помощью 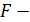 критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е.
критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. 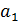 = 0, и, следовательно, фактор х не оказывает влияния на результат у.
= 0, и, следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету 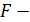 критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной y от среднего значения
критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной y от среднего значения 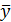 на две части — «объясненную» и «необъясненную»:
на две части — «объясненную» и «необъясненную»:
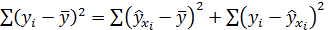 , (3.18)
, (3.18)
или 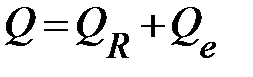 , (3.19)
, (3.19)
где 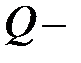 общая сумма квадратов отклонений зависимой переменной от средней;
общая сумма квадратов отклонений зависимой переменной от средней;
|
|
|
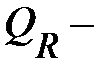 сумма квадратов отклонений, объясненная регрессией;
сумма квадратов отклонений, объясненная регрессией;
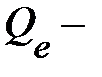 остаточная сумма квадратов отклонений, характеризующая влияние неучтенных факторов.
остаточная сумма квадратов отклонений, характеризующая влияние неучтенных факторов.
Общая сумма квадратов отклонений индивидуальных значений результативного признака y от среднего значения 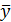 вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ох и
вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ох и 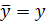 .Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
.Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат y. Это равносильно тому, что коэффициент детерминации 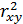 будет приближаться к единице.
будет приближаться к единице.
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим дисперсии:
|
|
|
общая дисперсия

обусловленная регрессией дисперсия
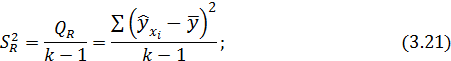
остаточная дисперсия
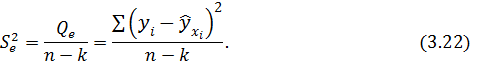
Для рассмотренного примера 4.2 соответствующие дисперсии будут равны:
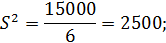
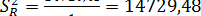 ;
;
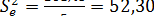 .
.
При отсутствии линейной зависимости между зависимой и объясняющей переменной случайные величины 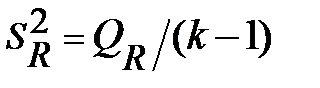 и
и 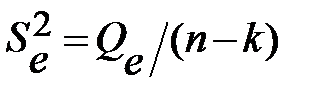 имеют
имеют 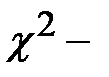 распределение соответственно с
распределение соответственно с 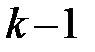 и
и 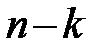 степенями свободы, а их отношение
степенями свободы, а их отношение 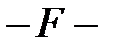 распределение с теми же степенями свободы [Ссылка]. Поэтому уравнение регрессии значимо на уровне значимости
распределение с теми же степенями свободы [Ссылка]. Поэтому уравнение регрессии значимо на уровне значимости 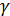 , если фактически наблюдаемое значение статистики
, если фактически наблюдаемое значение статистики
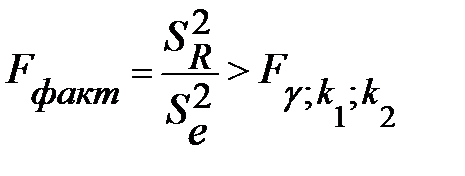 , (3.23)
, (3.23)
где 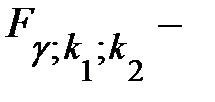 табличное значение
табличное значение 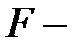 критерия Фишера – Снедекора,
критерия Фишера – Снедекора,
определенное на уровне значимости 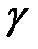 при
при 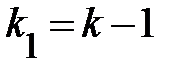 и
и 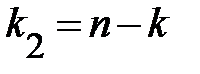 степенях свободы.
степенях свободы.
Учитывая смысл величин 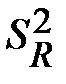 и
и 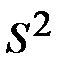 , можно сказать, что значение
, можно сказать, что значение 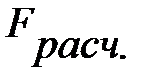 показывает, в какой мере регрессия
показывает, в какой мере регрессия 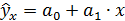 лучше оценивает значение зависимой переменной по сравнению с ее средней
лучше оценивает значение зависимой переменной по сравнению с ее средней  .
.
В случае линейной парной регрессии 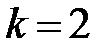 , поэтому
, поэтому 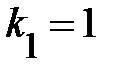 и
и 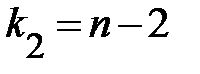 , и следовательно уравнение регрессии значимо на уровне
, и следовательно уравнение регрессии значимо на уровне 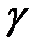 ,если
,если
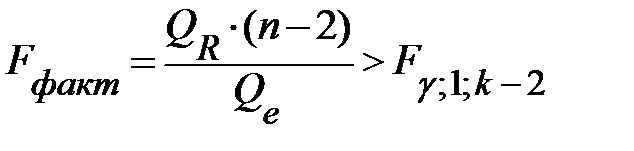 .
.
Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для 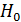 необходимо опровержение, чтобы обусловленная регрессией дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений
необходимо опровержение, чтобы обусловленная регрессией дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений 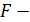 оотношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение
оотношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение 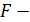 критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение
критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение 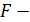 отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии признаков отклоняется и делается вывод о существенности этой связи:
отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии признаков отклоняется и делается вывод о существенности этой связи: 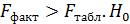 отклоняется.
отклоняется.
Если жевеличина окажется меньше табличной 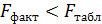 ,то нулевой гипотезы выше заданного уровня (например 0,05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае регрессии считается статистически незначимым.
,то нулевой гипотезы выше заданного уровня (например 0,05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае регрессии считается статистически незначимым. 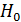 не отклоняется.
не отклоняется.
Предварительно для рассматриваемого примера 3.2 по формуле 4.23 определим расчетное значение 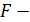 критерия:
критерия:
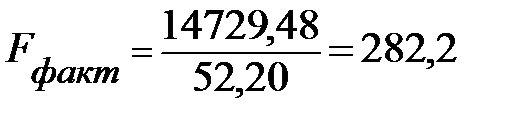 .
.
Для подтверждения или опровержения нулевой гипотезы на уровне значимости 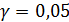 при
при 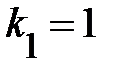 и
и 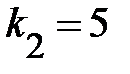 степенях свободы получим табличное значение
степенях свободы получим табличное значение 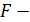 критерия:
критерия:
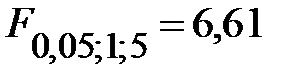 .
.
Поскольку 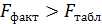 при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью для параметров уравнения парной регрессии определяются средние квадратические ошибки.
Средне квадратические ошибки коэффициентов регрессии 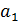 определяется на основании формулы:
определяется на основании формулы:
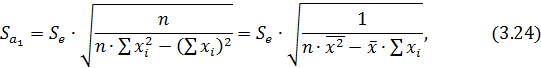
где 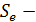 остаточная среднеквадратическая ошибка, вычисляемая на основании формулы (3.22).
остаточная среднеквадратическая ошибка, вычисляемая на основании формулы (3.22).
Для нашего примера 3.2 величины средней квадратической ошибки параметра 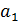 составит:
составит:
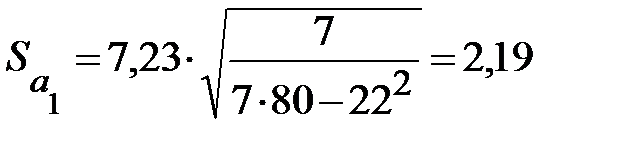 .
.
Величина среднеквадратических ошибок совместно с 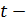 распределением Стьюдента при n — 2 степенях свободы применяется для проверки существенности коэффициентов парной регрессии и для расчета их доверительных интервалов.
распределением Стьюдента при n — 2 степенях свободы применяется для проверки существенности коэффициентов парной регрессии и для расчета их доверительных интервалов.
Для оценки существенности коэффициента парной регрессии его величина сравниваются с их среднеквадратическими ошибками, т. е. определяются фактические значения 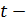 критерия Стьюдента. Фактические значения критерия – Стьюдента получают по формулам:
критерия Стьюдента. Фактические значения критерия – Стьюдента получают по формулам:
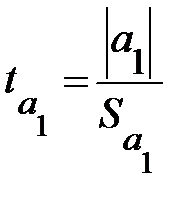 . (3.25)
. (3.25)
Для рассмотренного примера 3.2 рассчитаем фактическое значение 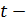 критерия Стьюдента для параметра
критерия Стьюдента для параметра 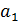 :
:
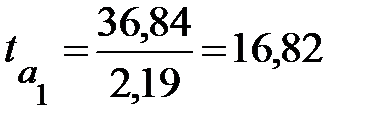 .
.
На уровне значимости 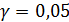 и числе степеней свободы
и числе степеней свободы 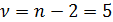 табличное значение
табличное значение 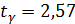 .Так как фактическое значение
.Так как фактическое значение 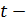 критерия превышает табличное, то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить.
критерия превышает табличное, то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить.
|
|
|
Этот же результат получим, извлекая квадратный корень из найденного ранее F -критерия, т. е.
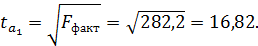
Табличное значение статистики Стьюдента используется для интервальной оценки коэффициентов регрессии. Например, доверительный интервал для параметра 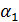 имеет вид:
имеет вид:
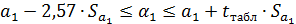 . (3.26)
. (3.26)
В условиях нашего примера 4.2 для коэффициента регрессии 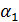 на уровне значимости
на уровне значимости 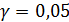 границы интервала составят:
границы интервала составят:
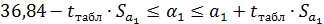
Для коэффициента регрессии 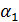 в примере 95 %-ные границы составят:
в примере 95 %-ные границы составят:
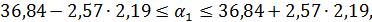
т. е.
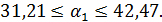
Аналогичным образом осуществляется оценка значимости коэффициента парной регрессии 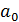 и его интервальная оценка.
и его интервальная оценка.
Среднеквадратическая ошибка параметра 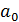 рассчитывается по формуле:
рассчитывается по формуле:
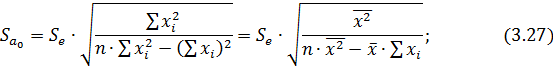
Методика оценки значимости этого параметра аналогично тому, что и для параметра 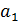 . То есть вычисляется расчетное значение
. То есть вычисляется расчетное значение 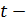 критерия Стьюдента:
критерия Стьюдента:
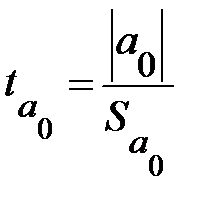 . (3.28)
. (3.28)
Его величина сравнивают с табличным значением 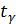 .
.
 2015-05-18
2015-05-18 2539
2539
