Что можно сделать в отношении автокорреляции?
Во-первых, определить фактор, ответственный за автокорреляцию, и включить его в уравнение регрессии. Но это практически невозможно.
Во-вторых, в случае автокорреляции, подчиненной авторегрессионному процессу 1-го порядка (т. е. 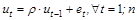 ), мы могли бы полностью устранить автокорреляцию, если бы знали величину
), мы могли бы полностью устранить автокорреляцию, если бы знали величину 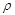 .
.
Предположим, что истинная модель задается выражением:
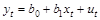 (2.4)
(2.4)
(t = 1; n).
Тогда наблюдение (t – 1) формируется как:
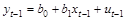 .
.

 Умножим полученное выражение на
Умножим полученное выражение на 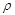 и вычтем его из обеих частей уравнения (2.4). В результате получим:
и вычтем его из обеих частей уравнения (2.4). В результате получим:
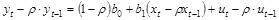 . (2.5)
. (2.5)
Обозначим 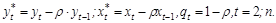
Тогда формулу (2.5) можно переписать как:
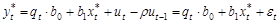
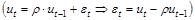 .
.
Значения 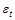 (случайной составляющей в модели зависимости ut от ut-1) для различных t не зависят друг от друга, поэтому проблемы автокорреляции остатков в полученном уравнении для преобразованных переменных нет. Параметры данного уравнения оцениваются обычным МНК. Получаем оцененную регрессию:
(случайной составляющей в модели зависимости ut от ut-1) для различных t не зависят друг от друга, поэтому проблемы автокорреляции остатков в полученном уравнении для преобразованных переменных нет. Параметры данного уравнения оцениваются обычным МНК. Получаем оцененную регрессию: 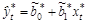 .
.
Затем определяются оценки параметров исходного уравнения регрессии (2.4): 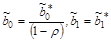 . Окончательно оцененное уравнение регрессии будет иметь вид:
. Окончательно оцененное уравнение регрессии будет иметь вид: 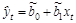 .
.
|
|
|
Однако, если в выборке нет данных, предшествующих 1-му наблюдению, мы не можем вычислить значения 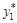 ,
, 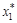 . Уменьшение числа степеней свободы на единицу приведет к потере эффективности, которая может в небольших выборках перевесить повышение эффективности от устранения автокорреляции. Эту проблему решают с помощью поправки Прайса-Уинстена:
. Уменьшение числа степеней свободы на единицу приведет к потере эффективности, которая может в небольших выборках перевесить повышение эффективности от устранения автокорреляции. Эту проблему решают с помощью поправки Прайса-Уинстена: 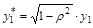 ,
, 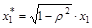 ,
, 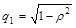 .
.
На практике величина 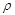 , конечно, неизвестна, его оценка получается одновременно с оценками параметров b0 и b1. В качестве оценки
, конечно, неизвестна, его оценка получается одновременно с оценками параметров b0 и b1. В качестве оценки 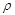 обычно используют выборочный коэффициент автокорреляции остатков 1-го порядка ret,et-1:
обычно используют выборочный коэффициент автокорреляции остатков 1-го порядка ret,et-1: 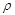 = ret,et-1.
= ret,et-1.
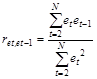 ,
, 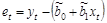 ,
,
где 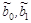 – МНК-оценки параметров b0, b1.
– МНК-оценки параметров b0, b1.
Другой способ оценки 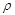 используется в методе Кохрейна-Оркатта. Алгоритм метода Кохрейна-Оркатта носит итеративный характер:
используется в методе Кохрейна-Оркатта. Алгоритм метода Кохрейна-Оркатта носит итеративный характер:
1) обычным МНК оценивается регрессия (2.4);
2) вычисляются остатки еt (t = 1; n);
3) оценивается регрессионная зависимость еt от
еt-1: 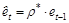 , коэффициент при еt-1, равный
, коэффициент при еt-1, равный 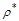 , представляет собой оценку ret,et-1;
, представляет собой оценку ret,et-1;
4) с этой оценкой (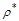 ) уравнение (2.4) преобразуется к виду:
) уравнение (2.4) преобразуется к виду:
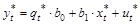 (2.6)
(2.6)
где 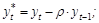
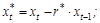
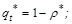
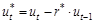 ;
;
5) обычным МНК оценивается уравнение (2.6):
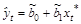 . Затем вычисляют оценки параметров исходного уравнения (2.4), как
. Затем вычисляют оценки параметров исходного уравнения (2.4), как 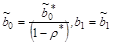 ;
;
6) повторно вычисляются остатки et и процесс возвращается к этапу 3.
Процесс обычно заканчивается, когда очередное приближение 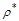 мало отличается от предыдущего. Иногда просто фиксируется количество итераций.
мало отличается от предыдущего. Иногда просто фиксируется количество итераций.
 Другой способ оценки
Другой способ оценки 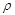 – метод Хилдрета-Лу:
– метод Хилдрета-Лу:
Для каждого значения 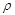 из определенного диапазона с заданным шагом внутри его оценивается преобразованное уравнение регрессии:
из определенного диапазона с заданным шагом внутри его оценивается преобразованное уравнение регрессии:
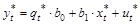 (2.7)
(2.7)
где 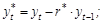
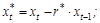
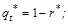
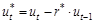 ;
;
Например, из диапазона от 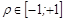 с шагом 0,01.
с шагом 0,01.
|
|
|
Значение 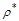 , которое дает минимальную сумму квадратов отклонений для преобразованного уравнения (2.7), принимается в качестве оценки
, которое дает минимальную сумму квадратов отклонений для преобразованного уравнения (2.7), принимается в качестве оценки 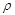 . Оценки коэффициентов исходного уравнения регрессии (2.4) определяются как
. Оценки коэффициентов исходного уравнения регрессии (2.4) определяются как 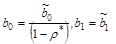 .
.
 2015-05-18
2015-05-18 679
679







