Линейное моделирование

Задача линейного программирования заключается в изучении способов отыскания наибольшего или наименьшего значении линейной функции при наличии линейных ограничений.

Задачи линейного программирования являются математическими моделями многочисленных задач экономического содержания.

Например, задача планирования работы предприятия.

Предприятие может выпускать n видов продукции; прибыльность единицы продукции вида j (j = 1, 2, …n) составляет с_j. В производстве используются ресурсы m видов (сырье, рабочая сила, энергия и т.д.). Наличие ресурса i (i = 1…m) ограничено величиной b_i. Расход ресурса i на производстве единицы продукции вида j составляет a_ij. Требуется определить производственную программу (т.е. требуется найти объемы выпуска x_j по каждому из видов продукции) таким образом, чтобы лимиты по ресурсам не были превышены, а суммарная прибыль была бы максимальной.

Формальная запись этих требований приводит к следующей задаче:

найти максимум линейной функции

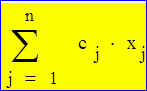
при ограничивающих условиях

где c_j, a_ij, b_i – заданные числа.

Определение 1. Функция, наибольшее или наименьшее значение которой отыскивается, называется целевой функцией.

Определение 2. Оптимальный план – совокупность значений переменных, при которых достигается наибольшее или наименьшее значения.

Определение 3. Всякая другая совокупность значений, удовлетворяющая ограничениям, определяет допустимый план (решение).

Линейные неравенства и область решений системы линейных неравенств

Пусть задано линейное неравенство с двумя переменными x₁ и x₂

a₁x₁ + a₂x₂ + b ³ 0.

Величины x₁ и x₂ будем рассматривать как координаты точки плоскости.

Определение 4. Совокупность точек плоскости, координаты которых удовлетворяют неравенству a₁x₁ + a₂x₂ + b ³ 0, называется областью решений данного неравенства.

Областью решений неравенства a₁x₁ + a₂x₂ + b ³ 0 является полуплоскость.

Для того, чтобы узнать, какая из двух полуплоскостей соответствует неравенству a₁x₁ + a₂x₂ + b ³ 0, достаточно привести это неравенство к виду

x₂ ³ kx₁ + d либо к виду x₂ £ kx₁ + d. В первом случае искомая полуплоскость лежит выше прямой a₁x₁ + a₂x₂ + b = 0, во втором случае – ниже ее.

В случае же, если задана система неравенств

a₁₁x₁ + a1₂x₂ + b₁ ³ 0

a2₁x₁ + a₂₂x₂ + b₂ ³ 0

………………….

a_m1x₁ + a _m2x₂ + b_m ³ 0,

где m - конечное число, то будем иметь пересечение конечного числа полуплоскостей, образующих многоугольную область D.

Определение 5. Область D называется областью решений данной системы неравенств.

Аналогично, можно геометрически интерпретировать и систему неравенств с тремя переменными

a₁₁x1 + a₁₂x₂ + a₁₃x₃ + b₁³ 0

a₂₁x1 + a₂₂x₂ + a₁₃x₃ + b₂³ 0

……………………………

a_m1x1 + a_m2x₂ + a_m3x₃ + b_m³ 0.

Каждое неравенство выполняется для одного из полупространств, на которые разбивает все пространство соответствующая плоскость. Данная система неравенств будет представлять собой пересечение полупространств, т.е. образуется многогранная областьрешений системы неравенств.

§ Пример

Найти полуплоскость, определяемую неравенством 2x₁ + 3x₂ -12 £ 0.

Решение.

Заменяя знак неравенства на знак точного равенства, получим уравнение прямой 2x₁ + 3x₂ -12 = 0 или x₂ = 2x₁ / 3 + 4.

Построим график прямой x₂ = 2x₁ / 3 + 4.

Для этого в Mathcad зададим функцию

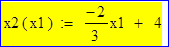
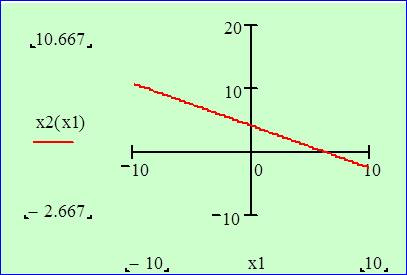
Данное неравенство приведем к виду x₂ £ 2x₁ / 3 + 4. Следовательно, искомая полуплоскость расположена ниже прямой x₂ = 2x₁ / 3 + 4.

§ Пример Найти область решений системы неравенств

x₁ – 1 ³ 0, x₂ -1 ³ 0, x₁ + x₂ -3 ³ 0, -6x₁ -7x₂ + 42 ³ 0.

Решение.

Заменяя знак неравенств на знаки точных равенств получим уравнения четырех прямых: x₁ – 1 = 0, x₂ -1 = 0, x₁ + x₂ -3 = 0,

-6x₁ -7x₂ + 42 = 0.

Построим графики этих четырех прямых:

В Mathcad зададим четыре функции:

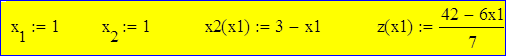
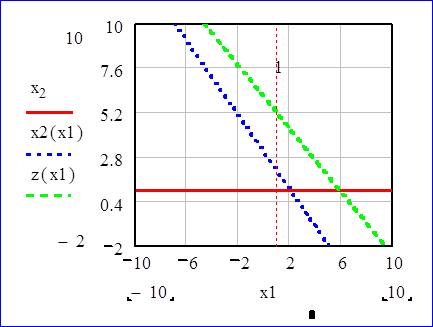
Областью решения является выпуклый четырехугольник, ограниченный на графике цветными линиями.