Пусть в пространстве в области 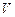 , ограниченной замкнутой поверхностью
, ограниченной замкнутой поверхностью 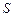 , задана непрерывная функция
, задана непрерывная функция 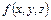 . Тогда интеграл
. Тогда интеграл
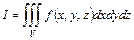 (40)
(40)
называется тройным интегралом от функции 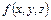 по области
по области 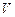 .
.
Если 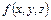 – плотность вещества, то интеграл
– плотность вещества, то интеграл 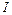 имеет смысл массы вещества, находящейся в объеме
имеет смысл массы вещества, находящейся в объеме 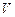 . Если
. Если 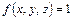 , то
, то
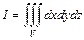 (41)
(41)
и интеграл (41) равен объему 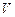 .
.
Вычисление тройного интеграла, аналогично двойному, делается сведением его к 3-х кратному интегралу. При этом область 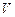 считается правильной, т.е. для нее выполняются следующие условия:
считается правильной, т.е. для нее выполняются следующие условия:
всякая прямая, параллельная оси 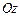 , проведенная в
, проведенная в 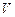 , пересекает поверхность
, пересекает поверхность 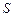 лишь в двух точках;
лишь в двух точках;
область 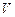 проецируется на плоскость
проецируется на плоскость 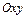 в правильную область
в правильную область 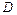 (т.е. любые прямые, параллельные осям
(т.е. любые прямые, параллельные осям 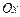 и
и 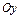 , проведенные в
, проведенные в 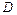 , пересекают границу
, пересекают границу 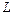 области
области 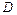 лишь в двух точках).
лишь в двух точках).
Сказанное в п. 2 справедливо для проекции 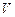 и на другие координатные плоскости (
и на другие координатные плоскости (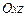 и
и 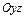 ).
).
Пусть поверхности 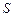 , ограничивающие область
, ограничивающие область 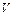 снизу и сверху, описываются уравнениями:
снизу и сверху, описываются уравнениями: 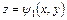 и
и 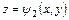 соответственно.
соответственно.
На границе 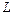 области
области 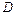 обозначим через
обозначим через 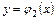 и
и 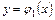 уравнения дуг
уравнения дуг 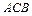 и
и 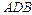 , а через
, а через 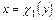 и
и 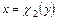 – уравнения дуг
– уравнения дуг 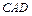 и
и 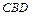 соответственно (рис. 5). Тогда интеграл (40) можно записать в виде 3 – х кратного интеграла
соответственно (рис. 5). Тогда интеграл (40) можно записать в виде 3 – х кратного интеграла
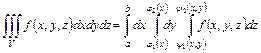 (42)
(42)
или
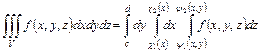 . (43)
. (43)
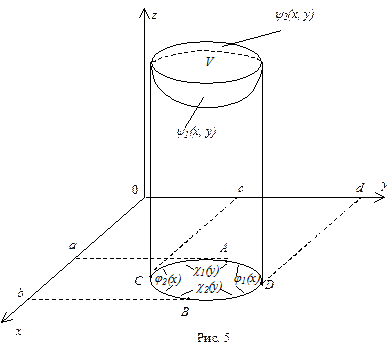
Пример 17. Вычислить интеграл 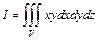 , где область
, где область 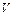 ограничена плоскостями
ограничена плоскостями 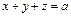 ,
, 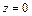 ,
, 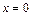 ,
, 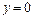 (рис. 6).
(рис. 6).

Область 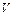 представляет собой пирамиду, верхняя поверхность которой описывается уравнением
представляет собой пирамиду, верхняя поверхность которой описывается уравнением 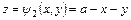 , а нижняя – уравнением
, а нижняя – уравнением 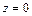 . Проекцией области
. Проекцией области 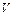 на плоскость
на плоскость 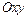 является треугольник, уравнение гипотенузы которого есть
является треугольник, уравнение гипотенузы которого есть 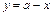 (это уравнение получается из уравнения
(это уравнение получается из уравнения 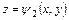 при
при 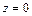 ). При интегрировании по
). При интегрировании по 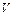 координата
координата 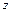 изменяется от
изменяется от 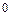 до
до 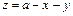 . При интегрировании по
. При интегрировании по 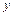 координата
координата 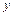 изменяется от
изменяется от 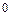 до
до 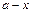 . Т.о., интеграл
. Т.о., интеграл 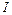 можно записать в виде 3–х кратного интеграла
можно записать в виде 3–х кратного интеграла
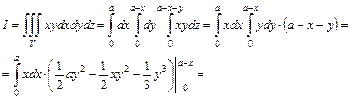
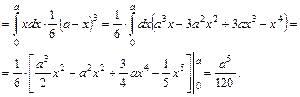
 2015-05-18
2015-05-18 408
408








