Если 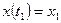 и
и 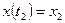 заданы, то равенство уравнение (2) обеспечивается при
заданы, то равенство уравнение (2) обеспечивается при 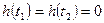
Если задано только 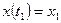 , а
, а 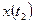 не задано, тогда
не задано, тогда 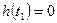 то равенство обеспечивается при
то равенство обеспечивается при
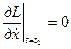
Если 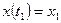 не задано, а
не задано, а 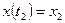 задано, тогда
задано, тогда 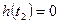 , то равенство уравнение (2) обеспечивается при
, то равенство уравнение (2) обеспечивается при 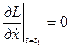
Если 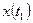 не задано и
не задано и 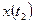 не задано то равенство уравнение)2) обеспечивается уравнением (2) обеспечивается при
не задано то равенство уравнение)2) обеспечивается уравнением (2) обеспечивается при
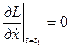 ,
, 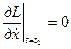
Обобщение на п- случай
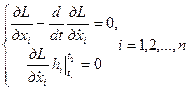
Пример: 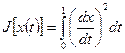 ,
, 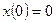 ,
, 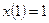
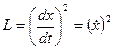
Уравнение 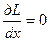 ,
, 
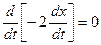 ,
, 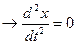
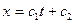 ,
, 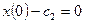 ,
, 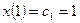
х=t
Т.е. 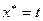
Проверка:
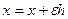 ,
, 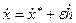
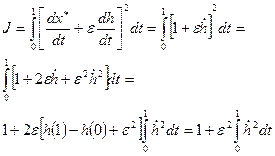
По условию 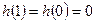
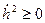 в любом случае, поэтому
в любом случае, поэтому 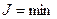 такие при
такие при 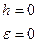
т. е при 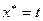
Вопрос 3. Синтез оптимальных систем методом динамического программирования.
В основе синтеза оптимального управления лежат два принципа:
-Синтез оптимального управления как функции времени и начального состояния системы (программное управление)
-Синтез оптимального управления как функции от текущих фазовых координат состояния ОУ и времени (управления по ОС)
Первое направление называется разомкнутой формой управления, второе замкнутой.
Наиболее предпочтительным является -второй принцип, его основана на методе динамического программирования предложенного Беллманом.
|
|
|
В основе динамического программирования лежит принцип оптимальности.
Рассмотрим оптимальную траекторию системы в трехмерном фазовом пространстве:
Начальное положение задается точкой А при 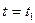
Конечное положение точкой В при 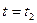
Пусть система перешла из т. А в т. С по оптимальной траектории (кривой 1)
Принцип гласит: что дальнейшее движение должно быть оптимальным (кривая 2). Т.е. независимо от того, каким образом система пришла в т.С. дальнейшее ее движение должно быть оптимальным.
Рассмотрим систему описываемую д.у.
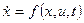 ,
, 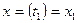 ,
, 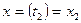
Управление и 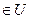 необходимо выбрать так, чтобы функционал качества
необходимо выбрать так, чтобы функционал качества
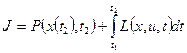 (1)
(1)
Рассмотрим некоторый момент времени 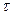
Если принять значение х(t) за начальное, то на интервале 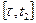 управление и(t) оптимальное в смысле минимума функционала J совпадает с оптимальным управлением и(t) для
управление и(t) оптимальное в смысле минимума функционала J совпадает с оптимальным управлением и(t) для 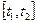
2 Вопрос вывод управления динамического программирования
На основании структуры функционала J определим оптимальную функцию стоимости (функция Беллмана)
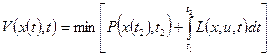 (2)
(2)
где 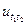 -это есть и(t) интервале
-это есть и(t) интервале 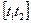
t-текущее время
Отсюда очевидно, что 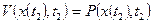
Допущение: V-непрерывна и имеет непрерывные частные производные до 20го порядка включительно.
Представим выражение в виде суммы

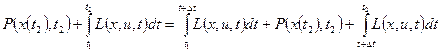
Таким образом: 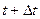
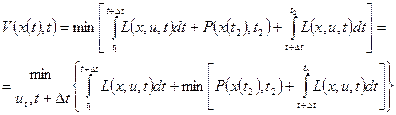 (3)
(3)
Это соотношение получено, исходя из принципа оптимальности 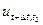 не зависит от предыстории не влияет на
не зависит от предыстории не влияет на 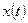
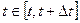
Второе слагаемое в (3) есть функция Беллмана
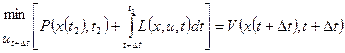
Таким образом,
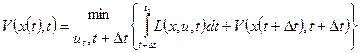 (4)
(4)
Поэтому = 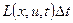
Второе слагаемое в (4) может быть разложено в ряд Тейлора
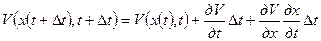 (5)
(5)
Подставляя (5) в (4) получим
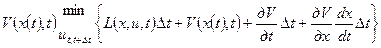

или (т.к. 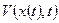 не зависит от и)
не зависит от и)
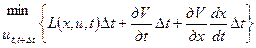
|
|
|
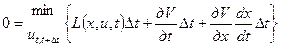 (6)
(6)
Разделим левую и правую часть на 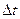 и устремляем его к нулю
и устремляем его к нулю 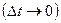 получим
получим
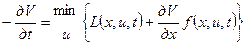 (7)
(7)
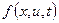 -функция которая определяет
-функция которая определяет 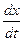
Уравнение (7) получено название динамического программирования или уравнения Гамильтона-Якоби-Беллмана.
Оно решается при граничном условии
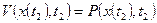 (8)
(8)
Т.о. для определения оптимального необходимо решить уравнение Беллмана с краевым условием (8)
Рассмотрим векторное обобщение:
Пусть 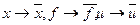
Поскольку V –функция стоимости, то V Т.о. уравнение Беллмана имеет вид
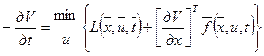 , (9)
, (9)
где
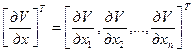 ,
, 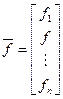 .
.
 2015-05-20
2015-05-20 194
194








