Цель расчета.
· По результату измерения массы груза (Опыт 1) и результатам измерения прогиба пружины определить модуль Юнга;
· Рассчитать стандартную неопределенность модуля Юнга;
· Записать результат измерения с указанием неопределенности.
Пример расчета
Исходные данные.
1 Результат измерения массы груза (Опыт 1).
· С расширенной неопределенностью при уровне доверия равном единице
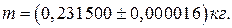
· Со стандартной неопределенностью
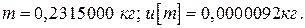
Результаты измерения прогиба пружины приведены в таблице 3.3.
Таблица 3.3 – результаты измерения прогиба пружины
| Номер измерения | ||||||||
| Прогиб, нм |
Продолжение таблицы 3.3
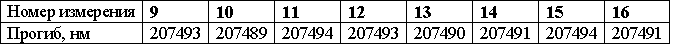
Внешний вид и сечение пружины показаны на рисунке 3.3, в таб. 3.4 даны геометрические размеры пружины.
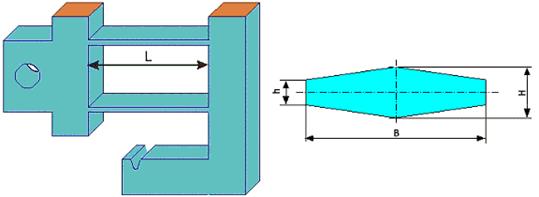
Рисунок 3.3 – Объект измерения
Таблица 3.4 – Геометрические размеры сечения пружины

4 Геометрические размеры пружины 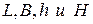 получены с использованием измерительного микроскопа с расширенной неопределенностью
получены с использованием измерительного микроскопа с расширенной неопределенностью
|
|
|
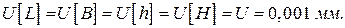
5 Ускорение свободного падения 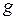 известно с расширенной неопределенностью
известно с расширенной неопределенностью 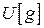
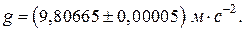
Решение
1 Вычисляем среднее значение прогиба
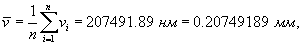
где 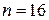 – число измерений.
– число измерений.
2 Определим среднеквадратическое отклонение результатов измерения
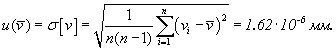
3 Вычислим момент инерции сечения пружины по формуле (1.1) теоретических сведений
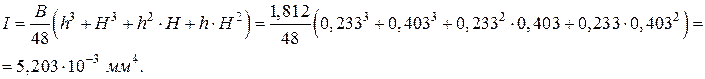
4 Оценим значение модуля Юнга по формуле (1.2) теоретических сведений
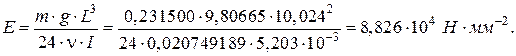
5 Определим комбинированную стандартную неопределенность оценки модуля Юнга.
Формула (1.1) содержит операции умножения, деления и возведения в степень, поэтому в качестве исходной формы для расчета неопределенности выбираем относительную неопределенность.
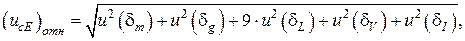 (3.1)
(3.1)
где индексы относительных неопределенностей в правой части соответствуют величинам аргументов. Основной операцией в формуле (7.1) является сложение, поэтому удобно в первую очередь определить абсолютную комбинированную стандартную неопределенность оценки момента инерции сечения
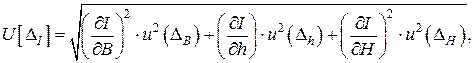 (3.2)
(3.2)
а затем вычислить относительную комбинированную стандартную неопределенность
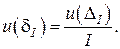 (3.3)
(3.3)
5.1 Определяем частные производные правой части уравнения (3.2)
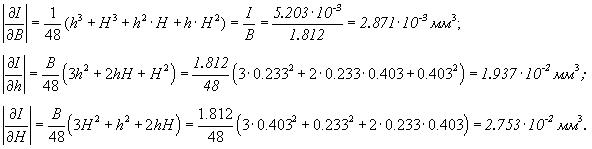
5.2 Определим комбинированную стандартную неопределенность оценки момента инерции сечения по формуле (3.2) с приписыванием составляющим погрешности равномерного распределения:
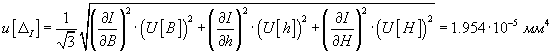
5.3 Вычислим относительную комбинированную стандартную неопределенность момента инерции сечения по формуле (3.3)
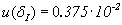 .
.
5.4 Определяем относительные комбинированные стандартные неопределенности, которые входят в правую часть формулы (3.1) при приписывании составляющим категории В равномерного распределения:
|
|
|
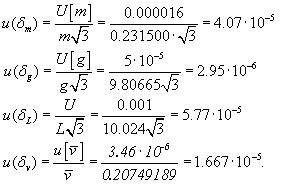
5.5 Вычисляем относительную комбинированную стандартную неопределенность оценки модуля Юнга по формуле (3.1)
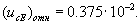
5.6 Вычислим комбинированную стандартную неопределенность модуля
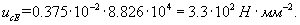
6 Запишем результат измерения с указанием комбинированной стандартной неопределённости
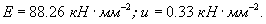
 2015-05-10
2015-05-10 292
292








