Тема: Исследование двумерной выборки.
Цель работы: научиться проводить корреляционный и регрессионный анализ заданной выборки.
Теоретические сведения.
При проведении корреляционного и регрессионного анализа, параметры могут подчиняться линейной и нелинейной зависимости.
Метод наименьших квадратов
Пусть на вход некоторого устройства подается сигнал х, а на выходе измеряется сигнал у, известно, что величины х и у связаны с функцией зависимостью, а какой именно – не известно. Требуется приближенно определить эту функцию, зависимость у= 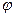 (х) по опытным данным.
(х) по опытным данным.
Пусть в результате n-измерений получен ряд экспериментальных точек х 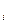 у
у 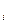 . Известно, что через n точек можно провести кривую аналитически, выражаемую многочленом (n-1), этот многочлен называется интерполяционным. Таким образом, замену функции f(x) на
. Известно, что через n точек можно провести кривую аналитически, выражаемую многочленом (n-1), этот многочлен называется интерполяционным. Таким образом, замену функции f(x) на 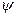 (x), так, что их значения совпадают в заданных точках называют, интерполяцией. Однако такое решение проблемы не является удовлетворительным, т.к. у от х часто отличаются из-за случайных ошибок. Поэтому у=
(x), так, что их значения совпадают в заданных точках называют, интерполяцией. Однако такое решение проблемы не является удовлетворительным, т.к. у от х часто отличаются из-за случайных ошибок. Поэтому у= 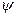 (х)+
(х)+ 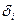 , где
, где 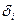 - некоторая случайная ошибка, поэтому требуется провести кривую, так чтобы она в наименьшей степени зависела от случайных ошибок. Это задача называется сглаживанием или аппроксимацией экспериментальной зависимости и часто решается она методом наименьших квадратов.
- некоторая случайная ошибка, поэтому требуется провести кривую, так чтобы она в наименьшей степени зависела от случайных ошибок. Это задача называется сглаживанием или аппроксимацией экспериментальной зависимости и часто решается она методом наименьших квадратов.
|
|
|
Задача аппроксимации решается следующем образом: в декартовой системе координат наносят точки х 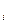 у
у 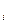 , по расположению этих точек высказывается предположение о принадлежности искомой функции к определенному классу функции.
, по расположению этих точек высказывается предположение о принадлежности искомой функции к определенному классу функции.
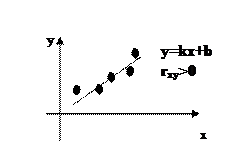
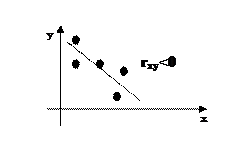
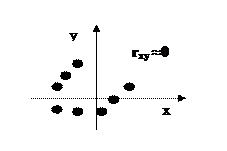
В общем случае 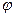 (х)=
(х)= 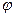 (х,
(х, 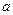
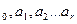 ), неизвестные параметры функции
), неизвестные параметры функции 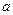
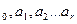 определяются из требования минимума суммы квадратов случайных ошибок. В случае линейной зависимости, необходимо найти таки параметры линии – коэффициент угла наклона и свободный коэффициент, при которых сумма квадратов отклонений всех точек от этой линии будет минимальна. Необходимый минимум величины
определяются из требования минимума суммы квадратов случайных ошибок. В случае линейной зависимости, необходимо найти таки параметры линии – коэффициент угла наклона и свободный коэффициент, при которых сумма квадратов отклонений всех точек от этой линии будет минимальна. Необходимый минимум величины 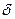 (суммарной невязки) является обращение в 0 частных производных невязки.
(суммарной невязки) является обращение в 0 частных производных невязки.
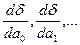
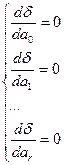
Решая систему из r-уравнений, находят неизвестные параметры а 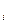 , которые наилучшим образом аппроксимируют искомую функцию
, которые наилучшим образом аппроксимируют искомую функцию 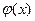 .
.
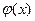 =
= 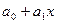
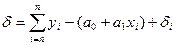
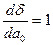
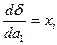
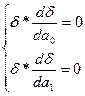
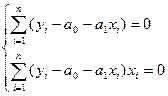
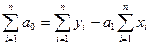
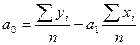
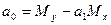
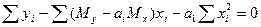
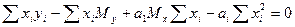
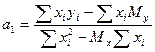
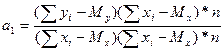
К 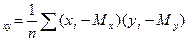
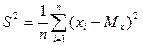
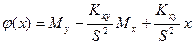
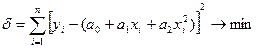
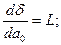
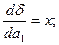
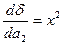
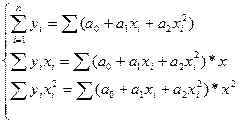
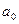 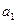 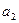
| |
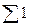 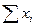 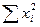
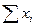 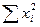 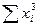
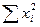 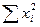 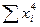
| 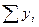
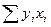
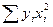
|
Имеем матричное уравнение, которое можно решить любым численным методом Гаусса (приводим матрицу к диагональному виду).
Ввиду простоты расчетов аппроксимации полиномами малых степеней используется довольно часто. Кроме того, многие функции, зависящие от двух параметров можно привести к линейному полиному. Для этого необходимо преобразовать исходную зависимость, в результате чего, она приобретает линейный вид.
|
|
|
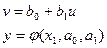
Далее решается задача линейной аппроксимации для новой зависимости, и вычисленные коэффициенты 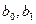 пересчитываются в коэффициенты
пересчитываются в коэффициенты 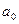 и
и 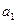 . Ряд возможных замен приводится в таблице:
. Ряд возможных замен приводится в таблице:
| Вид зависимости | Замена переменных | Ограничения | Обратная замена переменных | ||
Гиперболическая
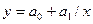
| v=y | u= 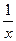
| x 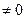
| a 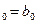
| a 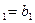
|
Логарифмическая
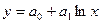
| v=y | u=lnx | x>0 | a 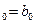
| a 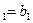
|
Показательная
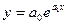
| v=lny | u=x | y>0
a 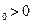
| a 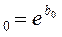
| a 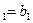
|
Степенная
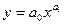
| v=lny | u=lnx | y>0
x>0
a 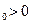
| a 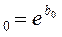
| a 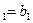
|
Комбинированная
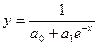
| v= 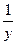
| u=e 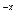
| y 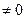
| a 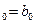
| a 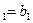
|
 2015-05-10
2015-05-10 560
560







