Средние значения

Плотность распределения вероятности дает полную информацию о свойствах случайной величины. Например, с помощью гистограммы несложно найти среднее значение.

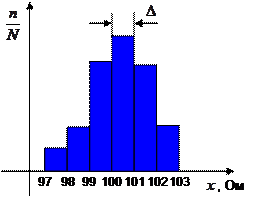
Вернемся к примеру с резисторами. Пусть у нас есть гистограмма, построенная по результатам испытаний, где отложены доли резисторов, сопротивление которых оказалось в данном интервале (см. рисунок). Как (приближенно) найти среднее значение сопротивления? Сложность в том, что мы не знаем сопротивлений отдельных резисторов и их количества. Тем не менее, гистограмма дает всю необходимую информацию.

Можно приближенно считать, что все резисторы, попавшие в интервал 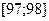(их количество равно 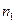), имеют сопротивление 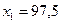Ом (середина интервала). Более точной информации все равно нет. Тогда общая сумма сопротивлений всех этих резисторов равна 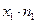. Повторяя те же рассуждения для остальных интервалов, получаем, что сумма сопротивлений всех резисторов равна 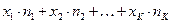, где 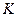– количество интервалов, а 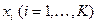– середина каждого из интервалов. Чтобы найти среднее значение, эту сумму нужно разделить на общее количество резисторов :

.

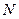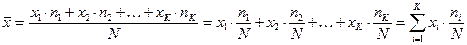Значения 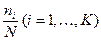– это доли от общего количества, то есть, высоты столбцов гистограммы. Таким образом, мы можем (приближенно) найти среднее значение по гистограмме, не зная ни сопротивлений отдельных резисторов, ни даже их количества.

В теории вероятности среднее значение 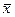называется математическим ожиданием случайной величины 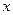и обозначается 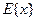. Если известна плотность распределения 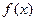, сумма заменяется интегралом

.

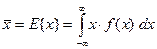Аналогично можно найти среднее значение любой функции, умножив ее на плотность распределения и проинтегрировав произведение на всей оси. Например, средний квадрат 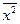вычисляется так

.

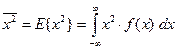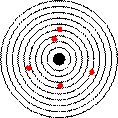
Среднее значение (математическое ожидание) не может полностью характеризовать случайную величину. На рисунках показаны мишени, пораженные двумя стрелками (каждый сделал по 5 выстрелов). В обоих случаях математическое ожидание – это центр мишени, то есть «в среднем» они бьют по центру. Однако всем понятно, что второй явно стреляет лучше. Как выразить это в виде числа?

У первого стрелка больше разброс точек попадания относительно средней точки. на языке теории вероятности разброс называется дисперсией – эта величина равна среднему квадрату отклонения от среднего значения 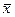. То есть, дисперсия вычисляется по формуле:

.

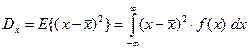Раскрыв скобки в подынтегральном выражении, можно показать, что дисперсия равна разности среднего квадрата и квадрата математического ожидания:

.

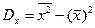Если математическое ожидание равно нулю, дисперсия и средний квадрат совпадают.

Использовать дисперсию не очень удобно, поскольку ее единицы измерения не совпадают с единицами измерения исходной величины (если 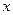измеряется в метрах, то дисперсия – в квадратных метрах). Поэтому на практике чаще применяют среднеквадратическое отклонение (СКВО) – квадратный корень из дисперсии:

.

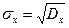В иностранной литературе эту величину называют стандартное отклонение.