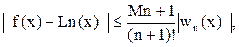Погрешность интерполяции (экстраполяции) в текущей точке

оценивается по формуле

(5)

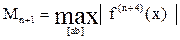где

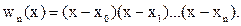(6)

(7)

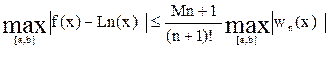Максимальная погрешность интерполяции на всем отрезке [a,в]:

(8)

1.1.1 Линейная интерполяция

Интерполяция по формуле (2) при n=1, т.е. с помощью линейной функции (3) называется линейной.

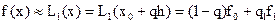Если ввести обозначения h=x₁-x₀, q=(x-x₀)/h, то по формула линейной интерполяции может быть записана в следующем виде:

(9)

Величина q называется фазой интерполяции, которая изменяется в пределах от 0 до 1, когда х пробегает значение от х₀ до х₁.

Геометрическая линейная интерполяция означает замену графика функции на отрезке [x₀, x₁] хордой, соединяющей точки (х₀,f₀), (х₁,f₁), как показано на нижеприведенном рисунке.

1.2 Сплайны

Пусть отрезок [a,b] разбит на N равных частичных отрезков [x_i,x_i+1], где x_j=a+ih, i=0,1,…,N-1; x_N=b, h=(b-q)IN.

Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a,b], а на каждом частичном отрезке [x_i,x_j+1] в отдельности является некоторым алгебраическим многочленом.

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной – дефектом сплайна.

На практике наиболее широко распространение получили кубические сплайны – сплайны третьей степени, имеющие на [a,b] непрерывную, по крайне мере, первую производную. Величина m_i=S¹₃(х) называется наклоном сплайна в точке (узле) х_i.

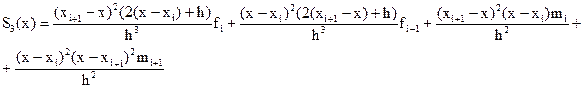(10)

Нетрудно убедится, что кубический сплайн S₃(x), принимающий в узлах x_i,x_i+1, соответственно значения f_i,f_i+1, имеет на частичном отрезке [x_i,x_i+1] вид

Действительно, легко видеть, что S₃(x_i)=f_i, S₃(x_i+1)=f_i+1. Кроме того, простые вычисления показывают, что S^’₃(x_i)= m_i, S^’₃(x_i+1)= m_i+1 Можно доказать, что любой алгебраический многочлен третьей степени, принимающий в точках x_i,x_i+1 значения, равные соответственно f_i,f_i+1 и имеющий в этих точках производную, соответственно равную m_i, m_i+1, тождественно совпадает с многочленом (10).

Итак, чтобы задать кубический сплайн S₃(x) на всем отрезке [a,b], нужно задать в N+1 узлах x_i его значения f_i и наклоны или касательные m_i, i=0,1,…,N.

Кубический сплайн, принимающий в узлах x_i те же значения, что и некоторая функция f называется интерполяционным. Он служит для аппроксимации функции f на отрезке [a,b] вместе с несколькими производными.

Способы задания наклонов интерполяционного кубического сплайна.

1) Упрощенный способ.

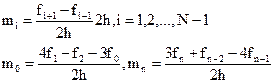(11)

2) Если известны значения f ^’_i производной f ^’ в узлах x_i, то полагаем m_i=f₁, i=0,1,…,N.

Способы 1 и 2 – локальные, так как с их помощью сплайн строится отдельно на каждом частичном отрезке[x_i,x_i+1].

2) Глобальный способ.

Обозначаем через S^”₃(x_i+0) значение S^”₃(x) в узле x_i справа, найденное непосредственно из выражения (10), а через S^”₃(x_i-0) значение S^”₃(x) в узле x_i слева, т.е. найденное из соответствующего выражения S₃(x) на частичном отрезке [x_i,x_i+1], которое получается из (10) заменой i на i-1.

Имеем

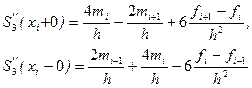Требуем непрерывности S^”(x) в узлах:

(12)

S^”₃(x_i-0)=S^”₃(x_i+0), i=1,2,…,N-1

и приходим к следующей системе линейных алгебраических уравнений относительно наклонов:

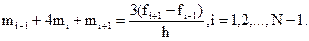Поскольку неизвестных N+1, то необходимо задать еще два условия, которые называются краевыми (они обычно связаны с крайними значениями m₀, и m_N). Дадим три варианта краевых условий.

а) Если известны f ^’₀=f ^’(a), f ^’_N=f ^’(b), то задать m₀=f ^’₀, m_N=f ^’_N.

б) Производные f ^’₀ и f ^’_N аппроксимируем формулами численного дифференцирования третьего порядка точности:

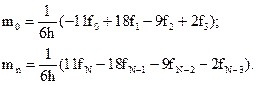(13)

в) В некоторых случаях бывают известны значения f ^’’ на концах отрезка [a,b],

т.е. величины f ^’’₀=f ^’’(a), f ^’’_N=f ^’’(b). Тогда требование S^”₃(а)=f ^’’₀ , S^”₃(b)=f ^’’_N приводит к краевым условиям:

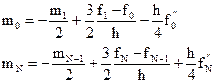(14)

Система (12) при всех рассматриваемых краевых условиях имеет единственное решение. Решая систему (12) при выбранных краевых условиях, находим наклоны m_i, i=0,1,…,N, во всех узлах.Затем по формуле (10) задаем сплайн на каждом частичном отрезке [x_i,x_i+1], i=0,1,…,N-1.

Построенный данным глобальным способом сплайн S₃(х) имеет дефект не больше единицы, т.к. этот сплайн обладает на отрезке [a,b] непрерывной второй производной.

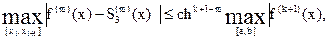Интерполяционный сплайн S₃(х) с наклоном, заданным способом 2 или 3, удовлетворяет неравенству

(15)

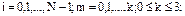где

с- независящая от h,i,f- постоянная.

Точность аппроксимации функции f сплайном S₃(х) управляется выбором N, т.е. шагом h=(b-a)/N.