К данному классу регрессий относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами. Примером таких нелинейных регрессий являются функции:
• степенная – 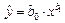
 ;
;
• показательная – 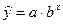 ;
;
• экспоненциальная – 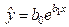 .
.
Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции и для оценки её параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.
Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении спроса от цен: 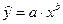 , где у — спрашиваемое количество; х — цена;
, где у — спрашиваемое количество; х — цена;
Данная модель нелинейна относительно оцениваемых параметров, т. к. включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду 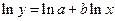 .Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой а и b могут быть найдены МНК.
.Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой а и b могут быть найдены МНК.
Широкое использование степенной функции 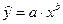 связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.
связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.
Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b.
Пример
По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х, млн. руб.).
| Y | |||||||
| X |
Требуется:
1. Для характеристики Y от Х построить следующие модели:
·линейную (для сравнения с нелинейными),
·степенную,
·показательную,
·гиперболическую.
· 2 .Оценить каждую модель, определив:
·индекс корреляции,
·среднюю относительную ошибку,
·F-критерий Фишера.
· 3 .Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.
· 4. Рассчитать прогнозные значения результативного признака по лучшей модели, если объем капиталовложений составит 89,573 млн. руб.
· 5. Результаты расчетов отобразить на графике.
Решение:
1. Построение линейной модели парной регрессии
Определим линейный коэффициент парной корреляции по следующей формуле:
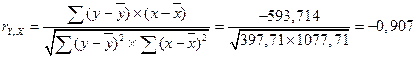 ;
;
Можно сказать, что связь между объемом капиталовложений 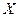 и объемом выпуска продукции
и объемом выпуска продукции  обратная, достаточно сильная.
обратная, достаточно сильная.
Уравнение линейной регрессии имеет вид: 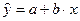 .
.
Таблица 3.5
| t | y | x | y´x | x´x | 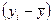 | 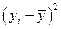 | 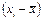 | 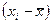 2 2 | 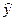 | 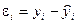 | 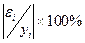 |
| 13.43 | 180.36 | -17.4 | 303.8 | 60.2 | 3.84 | 6.000 | |||||
| 5.43 | 29.485 | -13.4 | 180.36 | -1.96 | -3.500 | ||||||
| 1.43 | 2.0449 | 0.57 | 0.3249 | 50.3 | 1.74 | 3.346 | |||||
| -2.57 | 6.6049 | -5.43 | 29.485 | 53.6 | -5.56 | -11.583 | |||||
| -0.57 | 0.3249 | 2.57 | 6.6049 | 49.2 | 0.84 | 1.680 | |||||
| -4.57 | 20.885 | 14.57 | 212.28 | 42.6 | 3.44 | 7.478 | |||||
| -12.6 | 18.57 | 344.84 | 40.4 | -2.36 | -6.211 | ||||||
| И Итого | 0.01 | 397.71 | 1077.7 | -0.02 | 39.798 | ||||||
| ср.знач | 50.57 | 81.43 | 4033.14 | 6784.57 | 5.685 | ||||||
| диспер | 56.8 |
Значения параметров a и b линейной модели определим, используя данные таблицы 3.5
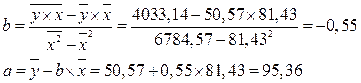
Уравнение линейной регрессии имеет вид: 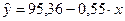 .
.
С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс. руб. Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения этого недостатка.
Рассчитаем коэффициент детерминации:
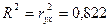 .
.
Вариация результата  (объема выпуска продукции) на 82,2 % объясняется вариацией фактора
(объема выпуска продукции) на 82,2 % объясняется вариацией фактора 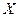 (объемом капиталовложений).
(объемом капиталовложений).
Оценку значимости уравнения регрессии проведем с помощью 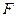 -критерия Фишера:
-критерия Фишера:
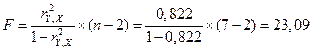
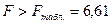 для a = 0,05,
для a = 0,05, 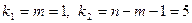
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. 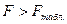 .
.
Определим среднюю относительную ошибку:
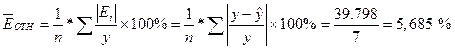
В среднем расчетные значения ŷ для линейной модели отличаются от фактических значений на 5,685 %.
2. Построение степенной модели парной регрессии
Уравнение степенной модели имеет вид: 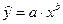 .
.
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
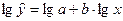 .
.
| Факт | Lg(Y) | Переменная | Lg(x) | |
| Y(t) | X(t) | |||
| 64.0 | 1.806 | 1.806 | ||
| 56.0 | 1.748 | 1.833 | ||
| 52.0 | 1.716 | 1.914 | ||
| 48.0 | 1.681 | 1.881 | ||
| 50.0 | 1.699 | 1.924 | ||
| 46.0 | 1.663 | 1.982 | ||
| 38.0 | 1.580 | 2.000 | ||
| 11.893 | 13.340 | |||
| Сред.знач. | 50.5714 | 1.699 | 81.429 | 1.906 |
Обозначим 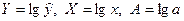 . Тогда уравнение примет вид:
. Тогда уравнение примет вид: 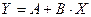 – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.6
– линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.6
Таблица 3.6
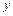 | 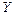 | 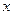 | 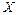 | 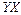 | 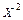 | 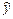 | 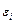 | 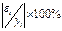 | 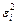 | |
| 1,8062 | 1,8062 | 3,2623 | 3,2623 | 61.294 | 2.706 | 4.23 | 7.322 | |||
| 1,7482 | 1,8325 | 3,2036 | 3,3581 | 58.066 | -2.066 | 3.69 | 4.270 | |||
| 1,7160 | 1,9138 | 3,2841 | 3,6627 | 49.133 | 2.867 | 5.51 | 8.220 | |||
| 1,6812 | 1,8808 | 3,1621 | 3,5375 | 52.580 | -4.580 | 9.54 | 20.976 | |||
| 1,6990 | 1,9243 | 3,2693 | 3,7029 | 48.088 | 1.912 | 3.82 | 3.657 | |||
| 1,6628 | 1,9823 | 3,2960 | 3,9294 | 42.686 | 3.314 | 7.20 | 10.982 | |||
| 1,5798 | 2,0000 | 3,1596 | 4,0000 | 41.159 | -3.159 | 8.31 | 9.980 | |||
| итог | 11,8931 | 13,3399 | 22,6370 | 25,4528 | 0,51 | 42.32 | 65.407 |
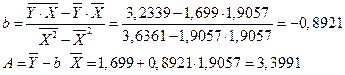
Уравнение регрессии будет иметь вид:
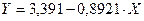 .
.
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.

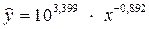 .
.
Получим уравнение степенной модели регрессии:
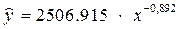 .
.
Определим индекс корреляции:
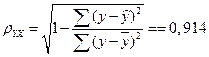 .
.
Связь между показателем y и фактором x можно считать достаточно сильной. Коэффициент детерминации: 0.836
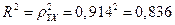
Вариация результата Y (объема выпуска продукции) на 83,6 % объясняется вариацией фактора Х (объемом капиталовложений).
Рассчитаем F-критерий Фишера:
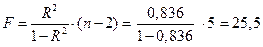 ;
;
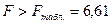 для a = 0,05,
для a = 0,05, 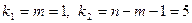
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. 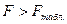 .
.
Средняя относительная ошибка
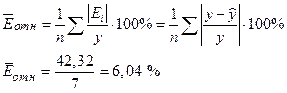 .
.
В среднем расчетные значения ŷ для степенной модели отличаются от фактических значений на 6,04 %.
3. Построение показательной функции
Уравнение показательной кривой: 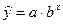 . Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
. Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения: 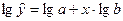 . Обозначим
. Обозначим 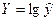 ,
, 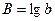 ,
, 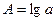 .
.
Получим линейное уравнение регрессии: 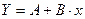 .
.
Рассчитаем его параметры, используя данные таблицы 3.7.
Таблица 3.7.
| t | 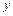 | 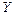 | 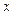 | 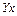 | 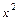 | 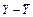 | 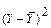  | 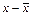 | 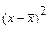 | 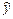 | 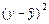 | 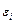 | 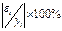 | ||||||
| 1,8062 | 115,60 | 0,1072 | 0,0115 | -17,43 | 303,76 | 60,6 | 11,464 | 3,3859 | 5,290 | ||||||||||
| 1,7482 | 118,88 | 0,0492 | 0,0024 | -13,43 | 180,33 | 3,9632 | -1,991 | 3,555 | |||||||||||
| 1,7160 | 140,71 | 0,0170 | 0,0003 | 0,57 | 0,33 | 49,7 | 5,4221 | 2,3285 | 4,478 | ||||||||||
| 1,6812 | 127,77 | -0,017 | 0,0003 | -5,43 | 29,47 | 53,1 | 25,804 | -5,08 | 10,583 | ||||||||||
| 1,6990 | 142,71 | 0,0000 | 0,0000 | 2,57 | 6,61 | 48,6 | 2,0031 | 1,4153 | 2,831 | ||||||||||
| 1,6628 | 159,62 | -0,036 | 0,0013 | 14,57 | 212,33 | 42,5 | 11,933 | 3,4544 | 7,509 | ||||||||||
| 1,5798 | 157,98 | -0,119 | 0,0142 | 18,57 | 344,90 | 40,7 | 7,3132 | -2,704 | 7,117 | ||||||||||
| иИтог | 11,8931 | 963,28 | 0,0300 | 1077,7 | 67,903 | 0,8093 | 41,363 | ||||||||||||
| ср знч | 50,57 | 1,6990 | 81,4 | 137,61 | 5,909 | ||||||||||||||
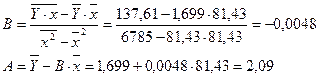
Уравнение будет иметь вид: Y=2,09-0,0048 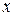 . Перейдем к исходным переменным
. Перейдем к исходным переменным 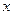 и
и 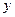 , выполнив потенциирование данного уравнения:
, выполнив потенциирование данного уравнения:
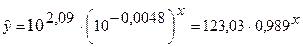 .
.
Определим индекс корреляции
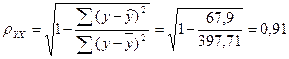 .
.
Связь между показателем 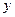 и фактором
и фактором 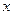 можно считать достаточно сильной.
можно считать достаточно сильной.
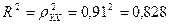
Вариация результата  (объема выпуска продукции) на 82,8 % объясняется вариацией фактора
(объема выпуска продукции) на 82,8 % объясняется вариацией фактора 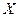 (объемом капиталовложений).
(объемом капиталовложений).
Рассчитаем F-критерий Фишера:
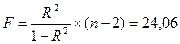
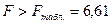 для a = 0,05,
для a = 0,05, 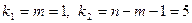 .
.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. 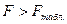 .
.
Средняя относительная ошибка:
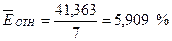
В среднем расчетные значения ŷ для показательной функции отличаются от фактических на 5.909 %.
4. Построение гиперболической функции
Уравнение гиперболической функции: 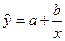 .
.
Произведем линеаризацию модели путем замены 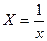 . В результате получим линейное уравнение
. В результате получим линейное уравнение 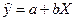 .
.
Рассчитаем его параметры по данным таблицы 3.8
Таблица 3.8.
| t | 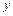 | 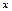 | 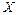 | 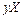 | 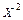 | 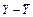 | 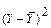  | 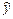 | 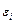 | 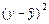 | 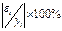 | |
| 0,0156 | 1,0000 | 0,0002441 | 13,43 | 180,33 | 61,5 | 2,489 | 6,1954 | 3,889 | ||||
| 0,0147 | 0,8235 | 0,0002163 | 5,43 | 29,47 | 58,2 | -2,228 | 4,9637 | 3,978 | ||||
| 0,0122 | 0,6341 | 0,0001487 | 1,43 | 2,04 | 49,3 | 2,740 | 7,5089 | 5,270 | ||||
| 0,0132 | 0,6316 | 0,0001731 | -2,57 | 6,61 | 52,7 | -4,699 | 22,078 | 9,789 | ||||
| 0,0119 | 0,5952 | 0,0001417 | -0,57 | 0.32653 | 48,2 | 1,777 | 3,1591 | 3,555 | ||||
| 0,0104 | 0,4792 | 0,0001085 | -4,57 | 20,90 | 42,9 | 3,093 | 9,5648 | 6,723 | ||||
| 0,0100 | 0,3800 | 0,0001000 | -12,57 | 158,04 | 41,4 | -3,419 | 11,69 | 8,997 | ||||
| иИтого | 0,0880 | 4,5437 | 0,0011325 | 397,71 | 354,2 | -0,246 | 65,159 | 42,202 | ||||
| ср знач | 50,57 | 0,0126 | 0,6491 | 0,0001618 | 6,029 | |||||||
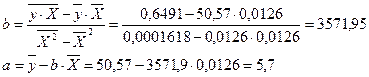 .
.
Получим следующее уравнение гиперболической модели:
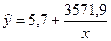 .
.
Определим индекс корреляции
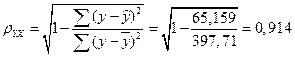 .
.
Связь между показателем y и фактором x можно считать достаточно сильной.
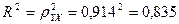
Вариация результата Y (объема выпуска продукции) на 83,5 % объясняется вариацией фактора Х (объемом капиталовложений).
F-критерий Фишера:
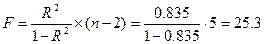
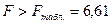 для a = 0,05,
для a = 0,05, 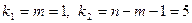 .
.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. 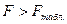 .
.
Средняя относительная ошибка
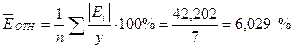
В среднем расчетные значения 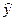 ŷ для гиперболической модели отличаются от фактических значений на 6,029 %.
ŷ для гиперболической модели отличаются от фактических значений на 6,029 %.
Для выбора лучшей модели построим сводную таблицу результатов.
 Таблица 3.9.
Таблица 3.9.
| Параметры Модель | Коэффициент детерминации R2 | F-критерий Фишера | Индекс корреляции ryx (ryx) | Средняя относительная ошибка Еотн |
| 1.Линейная | 0,822 | 23,09 | 0,907 | 5,685 |
| 2.Степенная | 0,828 | 24,06 | 0,910 | 6,054 |
| 3.Показательная | 0,828 | 24,06 | 0,910 | 5,909 |
| 4.Гиперболическая | 0,835 | 25,30 | 0,914 | 6,029 |
Все модели имеют примерно одинаковые характеристики, но большее значение 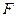 – критерия Фишера и большее значение коэффициента детерминации
– критерия Фишера и большее значение коэффициента детерминации 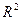 имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза.
имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза.
Показатель R2называется индексом детерминации. Он выражает долю факторной дисперсии, т. е. характеризует, какая часть общей вариации результативного признака у объясняется изучаемым фактором х.
Коэффициент детерминации используется для количественного определения характеристики, связывающей две переменные. Дает пропорцию общего изменения одной переменной (Y), которую можно объяснить изменением второй переменной (Х). Иногда R2 =1, но при этом связь отсутствует, поскольку Х и Y связаны с третьей переменной (Х2). Теоретическое корреляционное отношение: 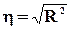 .
.
Индекс корреляции R определяется по формуле:
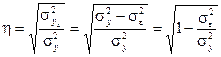 .
.
| Методы оценки тесноты связи |


| Корреляционный метод | Непараметрический метод |



| Парная | Множественная регрессия |
Коэффициент ассоциации 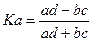 |
 |  | ||||
 | |||||
Индекс детерминации 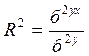 | Коэффициент множественной детерминации 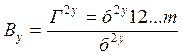 |
Коэффициент контингенции К.Пирсона 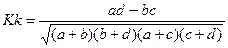 |
 |
Коэффициент Спирмена 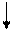  |


Индекс корреляции 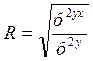 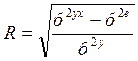 | Коэффициент частной корреляции 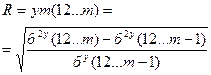 |
Коэффициент взаимной сопряженности К.Пирсона 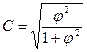 |
 |  |  | |||
Линейный коэффициент корреляции 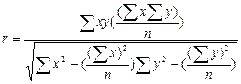 | Совокупный коэффициент множественной корреляции 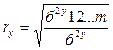 |
Коэффициент взаимной сопряженности А.А.Чупрова 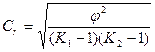 |

Коэффициент Кендэле 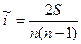 |

 2015-05-13
2015-05-13 1880
1880
