Связи.
Связи или ограничения это обычно различного рода закрепления системы: подшипники для валов машин, шарнирные опоры, жесткие или упругие заделки концов стержней или балок, опорные поверхности. Считают, что влияние связей на положение и движение материальных точек осуществляется посредством действия реакций связей. Приложив к точкам системы реакции связей, формально ее можно рассматривать как свободную систему точек.
Связи подразделяют на голономные и неголономные связи, а также зависящие и независящие от времени.
Обобщенные координаты
Допусти, что некоторая система состоит из N точек, на которые наложены голономные связи. Положение системы в момент времени t определяют 3 N координат точек уравнения связей
fv (xk, yk, zk, t) = 0 (v = 1, 2, ……., l).
Причем l < 3N.
В этом случае l координат могут быть выражены через остальные (3 N - l) независимые координаты, которым можно давать любые (достаточно малые) изменения без нарушения связей. Вариации этих независимых координат однозначно определяют вариации остальных зависимых координат. Число независимых координат системы, подчиненной только голономным связям, определяет число степеней свободы системы.
|
|
|
Числом степеней свободы системы с голономными связями называют число независимых обобщенных координат, через которые можно выразить декартовы координаты всех точек системы.
Вместо декартовых координат в качестве «независимых координат» выбирают обычно другие, связанные с ним величины, иногда другой физической природы и другой размерности. Эти независимые величины называют обобщенными координатами. Далее будем их обозначать через
q1, q2, ……., qn,
где n = 3N – l.
Число обобщенных координат должно быть равно числу независимых величин, однозначно определяющих положение системы, и через них должны выражаться все декартовы координаты системы в форме, например, уравнений
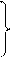 xi = xi (q1, q2,…….., qn, t),
xi = xi (q1, q2,…….., qn, t),
yi = yi (q1, q2,…….., qn, t), (i = 1, 2,……., N).
zi = zi (q1, q2,…….., qn, t)
Если голономные связи не зависят явно от времени t, то формулы, выражающие декартовы координаты через обобщенные координаты, не будут содержать времени явно. Так как радиус-вектор rk каждой точки системы выражается векторным образом через координаты этой точки в виде rk = xk l + yk j + zk k, то, следовательно, радиус-вектор каждой точки тоже является функцией, но векторной, от обобщенных координат и времени при реономных связях, так же как и проекции его xk, yk, zk:
rk = rk (q1, q2,…….., qn, t)
Таким образом, чтобы найти траекторию движения данной системы и закон движения по ней каждой точки, достаточно найти сначала в функциях времени все обобщенные координаты qi, а затем выразить все декартовы координаты в функциях времени. Тем самым установить закон движения системы.
|
|
|
Обобщенные силы
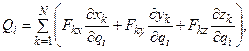 Обобщенная сила Qi, соответствующая обобщенной координате qi
Обобщенная сила Qi, соответствующая обобщенной координате qi
где Fkx, Fky, Fkz – проекции равнодействующих всех активных сил на оси координат; n – число степеней свободы; q 1, q 2 ……, qn – обобщенные координаты рассматриваемой системы.
Размерность обобщенной силы зависит от размерности обобщенной координаты. Если обобщенная сила имеет размерность длины, то обобщенная сила имеет размерность физической силы [Н]. Если же обобщенная координата имеет размерность угла [рад], то обобщенная сила Qi имеет размерность момента силы.
Принцип Даламбера.
Принцип Даламбера для свободной материальной точки эквивалентен основному закону динамики (второй закон Ньютона). Для несвободной материальной точки он эквивалентен основному закону динамики вместе с аксиомой связей и имеет вид
m w = F+R,
где F – равнодействующая активных сил; R – равнодействующая реакций связей; w – ускорение точки относительно инерциальной системы отсчета.
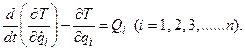 Уравнение Лагранжа второго рода
Уравнение Лагранжа второго рода
Составление уравнений Лагранжа выполняется в следующем порядке:
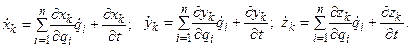
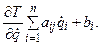 1. Взять частную производную от кинетической энергии по обобщенной скорости
1. Взять частную производную от кинетической энергии по обобщенной скорости
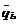 2. Взять полную производную по времени от этого выражения. Результатом будут вторые производные по времени
2. Взять полную производную по времени от этого выражения. Результатом будут вторые производные по времени
т. е. обобщенные ускорения. Так как коэффициенты aij зависят и от t, то от дифференцирования появляются и обобщенные скорости. Обобщенные ускорения войдут линейно, в первых степенях, а обобщенные скорости в общем случае нелинейно; так же нелинейно в зависимости от вида коэффициентов aij, bi, c и обобщенных сил войдут обобщенные координаты qi.
3. Составить частную производную ∂T/∂qi от кинетической энергии по обобщенной координате, которая так же входит в уравнения Лагранжа, дифференцируя коэффициенты aij, bi, c по qi.
4. Найти выражения обобщенных сил по данным силам, приложенным к точкам системы.
Получим систему уравнений Лагранжа второго рода, состоящую из n обыкновенных дифференциальных уравнений второго порядка относительно обобщенных координат.
Для определения обобщенных координат как функции времени необходимо произвести интегрирование уравнений Лагранжа
qi = qi (t, C1, C2, ……., C2n), i = 1, 2,..., n.
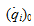 Произвольные интегрирования (C1, C2, ……., C2n) определяются исходя из начальных условий при t = 0, т.е. задаем соответствующие значения обобщенных координат (qi)0 и обобщенных скоростей.
Произвольные интегрирования (C1, C2, ……., C2n) определяются исходя из начальных условий при t = 0, т.е. задаем соответствующие значения обобщенных координат (qi)0 и обобщенных скоростей.
Зная обобщенные координаты и обобщенные скорости в функции времени, окончательно определяем декартовы координаты всех точек системы и их скорости по следующим зависимостям
Уравнения Лагранжа в случае потенциальных сил
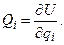 Силы, действующие на механическую систему, в этом случае могут быть выражены через силовую функцию U; обобщенные силы выражаются по формулам
Силы, действующие на механическую систему, в этом случае могут быть выражены через силовую функцию U; обобщенные силы выражаются по формулам
Уравнения Лагранжа принимают вид
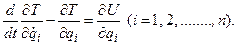 |
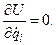
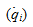 Замечая, что силовая функция U зависит только от обобщенных координат qi, но не зависит от обобщенных скоростей
Замечая, что силовая функция U зависит только от обобщенных координат qi, но не зависит от обобщенных скоростей
, следовательно
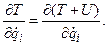 Соответственно
Соответственно
Вследствие этого каждое уравнение Лагранжа примет вид
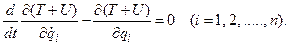 |
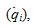 Введем функцию Лагранжа L = T + U, причем
Введем функцию Лагранжа L = T + U, причем
L = L (qi, t). Тогда уравнения Лагранжа окончательно примут вид
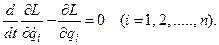 |
Механическая энергия системы Е равна
E = T – U = T + П.
А функция Лагранжа L не является механической энергией системы L = T – П.
 2015-05-13
2015-05-13 427
427







