Список основных равносильностей алгебры высказываний состоит из двух столбцов, один из которых получается заменой дизъюнкции на конъюнкцию и наоборот в другом столбце (0 на 1 и 1 на 0). Это не случайно, а является следствием закона двойственности.
Определение. Пусть F булева формула, т.е. формула, не содержащая импликаций, двойственной F* формулой называется формула, полученная из F заменой дизъюнкции на конъюнкцию и наоборот, а также 0 заменяется на 1 и 1 - на 0. Ясно, что (F*)*= F.
Теорема 1. Пусть F(x1,...,xk) - булева формула алгебры высказываний, зависящая от элементарных высказываний x1, x2,...,xk. Тогда отрицание формулы равносильно двойственной формуле от отрицаний, т.е. 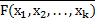 =F*(
=F*(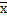 1,
1, 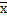 2,...,
2,..., 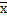 k)
k)
Теорема 2. Две формулы равносильны FºG тогда и только тогда, когда равносильны двойственные им F*ºG*.
Доказательство этих теорем основывается на законах де Моргана, которые являются частным случаем теоремы 1. Заметим, что F*(х1, х2,...,хk)ºF*(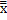 1,
1, 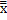 2,...,
2,..., 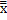 k)= F
k)= F 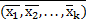 . Это позволяет проще строить двойственную функцию для функции F, заданной своими значениями.
. Это позволяет проще строить двойственную функцию для функции F, заданной своими значениями.
Пример 1. Для функции F=(0,0,1,0) построить двойственную.
1 способ. Функция F принимает значение 1 только для набора с номером 2, т.е. (1, 0). Значит, F=x`y. Тогда F*=xÚ`y. F* принимает значение 1 для наборов (0, 0), (1, 0), (1, 1), т.е. F*=(1, 0, 1, 1).
2 способ. Если F зависит от k переменных, то набор их значений мы условились располагать, используя двоичную запись порядка набора, начиная с 0 до 2k-1. Для набора переменных (`х1, `х2,...,`хk) эта последовательность будет в обратном порядке. Так, для k=2 последовательность значений вектора (x1, x2) будет (0, 0), (0, 1), (1, 0), (1, 1). Для вектора (`х1,`х2) ей будет соответствовать последовательность значений (1, 1), (1, 0), (0, 1), (0, 0). Кроме того, если F=1, то`F=0 и наоборот. Отсюда такое правило: последовательности значений F сопоставим последовательность, для которой в обратном порядке 0 заменится на 1, а 1 - н а 0. Для данной функции F это будет (1, 0, 1, 1), и это функция F*. Получаем тот же результат.
Пример 2. Для функции F=(0, 1, 0, 1, 1, 1, 0, 1) построить двойственную.
Ответ: F*=(0, 1, 0, 0, 0, 1, 0, 1).
Замечание. Теоремы двойственности упрощают построение КНФ, если ДНФ, равносильная данной формуле, уже построена.
Итак, пусть FºF1, где F1 - ДНФ. Тогда F1* - КНФ. Раскрыв скобки, приведём F1* к равносильной ей ДНФ. F1*ºF2 и F2 - ДНФ. Тогда F1=(F1*)*ºF2*. Значит FºF1ºF2* уже КНФ.
Пример 3. Найти ДНФ и КНФ, равносильные формуле F=(x`y«z)Úyz.
Решение. Найдём сначала равносильную булеву формулу.
Fº(x`yzÚ  z)Úyzº(x`yzÚ(`xÚ
z)Úyzº(x`yzÚ(`xÚ 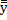 )`z)Úyzºx`yzÚ`x`zÚy`zÚyzºx`yzÚ`x`zÚy=F1 это ДНФ.
)`z)Úyzºx`yzÚ`x`zÚy`zÚyzºx`yzÚ`x`zÚy=F1 это ДНФ.
Здесь y 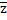 Úyz=y(`zÚz)ºy×1ºy.
Úyz=y(`zÚz)ºy×1ºy.
F1*=(xÚ`yÚz)(`xÚ`z)yº(x`xÚx`zÚ`y`xÚ`y`zÚz`xÚz`z)yºx`zyÚ`y`xyÚ`y`zyÚz`xyºxy`zÚ`xyz=F2[`xx=z`z=`y`xy=`y`zy=0]. Теперь F2*=(xÚyÚ`z)(`xÚyÚz)º(F1*)*=F1ºF
F2* - КНФ и СКНФ.
 2015-05-13
2015-05-13 1316
1316








